![]() žõź
žõź
ÍłįŪēėŪēôžóźžĄú žõź(Śúď, žėĀžĖī: circle)žĚÄ ŪŹČŽ©ī žúĄžĚė Ūēú ž†źžóź žĚīŽ•īŽäĒ ÍĪįŽ¶¨ÍįÄ žĚľž†ēŪēú ŪŹČŽ©ī žúĄžĚė ž†źŽď§žĚė žßĎŪē©žúľŽ°ú ž†ēžĚėŽźėŽäĒ ŽŹĄŪėēžĚīŽč§. žĚīŽü¨Ūēú ž†źžĚĄ žõźžĚė ž§Ďžč¨žĚīŽĚľÍ≥† ŪēėÍ≥†, ž§Ďžč¨Í≥ľ žõź žúĄžĚė ž†źžĚĄ žěáŽäĒ žĄ†Ž∂Ą ŽėźŽäĒ žĚīŽď§žĚė Í≥ĶŪÜĶŽźú ÍłłžĚīŽ•ľ žõźžĚė ŽįėžßÄŽ¶ĄžĚīŽĚľÍ≥† ŪēúŽč§.
žõźžĚÄ žĚīžį® Í≥°žĄ†žĚė žĚľžĘ̳֞ ŪÉÄžõźžóźžĄú žĚīžč¨Ž•†žĚī 0žĚł Í≤ĹžöįžĚīŽč§.
žö©žĖī
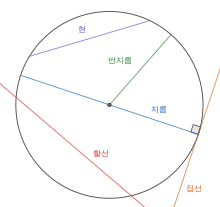 ŪėĄ, žßÄŽ¶Ą, ŽįėžßÄŽ¶Ą, Ūē†žĄ†, ž†ĎžĄ†
ŪėĄ, žßÄŽ¶Ą, ŽįėžßÄŽ¶Ą, Ūē†žĄ†, ž†ĎžĄ†
 Ūėł, ŪôúÍľī, Ž∂ÄžĪĄÍľī
Ūėł, ŪôúÍľī, Ž∂ÄžĪĄÍľī
žõźÍ≥ľ ÍīÄŽ†®Žźú ÍłįŽ≥łž†ĀžĚł žö©žĖīŽď§žĚÄ Žč§žĚĆÍ≥ľ ÍįôŽč§.
- Žč®žúĄžõź: ŽįėžßÄŽ¶ĄžĚī 1žĚł žõź
- ŽŹôžč¨žõź: ž§Ďžč¨žĚī ÍįôžĚÄ ŽĎź žõź
- Žįėžõź: ž§Ďžč¨ÍįĀžĚī ŪŹČÍįĀžĚł Ž∂ÄžĪĄÍľī(ŪôúÍľī)
- ŽįėžßÄŽ¶Ą: žõźžĚė ž§Ďžč¨Í≥ľ Í∑ł žõź žúĄžĚė ž†źžĚĄ žěáŽäĒ žĄ†Ž∂Ą ŽėźŽäĒ Í∑ł žĄ†Ž∂ĄžĚė ÍłłžĚī. ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīŽäĒ žßÄŽ¶ĄžĚė 2Ž∂ĄžĚė 1žĚīŽč§.
- Ž∂ÄžĪĄÍľī: ŽĎź ÍįúžĚė ŽįėžßÄŽ¶ĄÍ≥ľ ŪēėŽāėžĚė ŪėłŽ°ú ŽĎėŽü¨žčłžĚł žėĀžó≠
- žā¨Ž∂Ąžõź: ž§Ďžč¨ÍįĀžĚī žßĀÍįĀžĚł Ž∂ÄžĪĄÍľī
- žõźž£ľ: žõźžĚė ŽĎėŽ†ą
- žõźž£ľÍįĀ: Ūēú ŽĀĚž†źžĚĄ Í≥Ķžú†ŪēėŽäĒ ŽĎź ŪėĄžĚī žõź ŽāīŽ∂Ğ󟞥ú žĚīŽ£®ŽäĒ ÍįĀ. ŪĀ¨ÍłįŽäĒ žĚīžóź ŽĆÄžĚĎŪēėŽäĒ ž§Ďžč¨ÍįĀžĚė 1/2žĚīŽč§.
- žõźŪĆź: žõźžúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėē
- žõźŪôė: ŽĎź ŽŹôžč¨žõźžúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėē
- ž†ĎžĄ†: žõźÍ≥ľ Ūēú ž†źžóźžĄú ŽßĆŽāėŽäĒ žßĀžĄ†
- ž†ĎŪėĄÍįĀ: žõźžĚė ŪėĄÍ≥ľ ŪėĄžĚė Ūēú ŽĀĚž†źžóźžĄúžĚė ž†ĎžĄ†žĚī žĚīŽ£®ŽäĒ ÍįĀ
- ž§Ďžč¨: žõź žúĄžĚė žěĄžĚėžĚė ž†źžóź žĚīŽ•īŽäĒ ÍĪįŽ¶¨ÍįÄ žĚľž†ēŪēú Í∑ł žõźžĚĄ ŪŹ¨Ūē®ŪēėŽäĒ ŪŹČŽ©ī žúĄžĚė ž†ź
- ž§Ďžč¨ÍįĀ: ŪėłžĚė ŽĎź ŽĀĚž†źžĚĄ žßÄŽāėŽäĒ ŽįėžßÄŽ¶ĄžĚī ŪėłžôÄ ÍįôžĚÄ ž™ĹžóźžĄú žĚīŽ£®ŽäĒ ÍįĀ. ŪĀ¨ÍłįŽäĒ žĚīžóź ŽĆÄžĚĎŪēėŽäĒ žõźž£ľÍįĀžĚė 2ŽįįžĚīŽč§.
- žßÄŽ¶Ą: žõźžĚė ž§Ďžč¨žĚĄ žßÄŽāėŽäĒ ŪėĄ ŽėźŽäĒ Í∑ł ÍłłžĚī. ÍłłžĚīŽäĒ ŽįėžßÄŽ¶ĄžĚė 2ŽįįžĚīŽč§.
- žľ§Ž†ąŪėł: žõźžĚė Ūē©Ūēėžó¨ žõźž£ľ ž†Ąž≤īŽ•ľ žĚīŽ£®ŽäĒ ŽĎź Ūėł
- Ūē†žĄ†: žõźÍ≥ľ ŽĎź ž†źžóźžĄú ŽßĆŽāėŽäĒ žßĀžĄ†
- ŪėĄ: žõź žúĄžĚė ŽĎź ž†źžĚĄ žěáŽäĒ žĄ†Ž∂Ą
- Ūėł: žõźžĚė žĚľŽ∂ÄÍįÄ ŽźėŽäĒ Í≥°žĄ†
- ŪôúÍľī: ÍįôžĚÄ ŽĀĚž†źžĚĄ ÍįĖŽäĒ ŪėłžôÄ ŪėĄžúľŽ°ú ŽĎėŽü¨žčłžĚł žėĀžó≠
- žčú: Ūē†žĄ†žĚė ž§Ďž†źžĚĄ žąėžĄ†žĚė ŽįúŽ°ú ŪēėŽäĒ žĄ†
žó≠žā¨
Íłįžõźž†Ą 5žĄłÍłįÍ≤Ĺ žēąŪčįŪŹįžĚÄ ž†ēŽč§ÍįĀŪėēžĚė Ž≥Ä žąėŽ•ľ Í≥ĄžÜć ŽäėŽ†§ÍįÄŽ©ī Í≤įÍĶ≠žóĒ žõźžĚī ŽźúŽč§Í≥† žÉĚÍįĀŪĖąŽč§. žĚīžóź 15žĄłÍłį ŽŹÖžĚľžĚė žč†Ūēôžěź ŽčąžĹúŽĚľžöįžä§ŽäĒ žēĄŽ¨īŽ¶¨ Ž≥Ğ̥ ŽäėŽ†§ŽŹĄ žõźžĚī Žź† žąėŽäĒ žó܎觎äĒ žā¨žÉĀžúľŽ°ú ŽįėŽįēŪĖąŽč§.
ŪēīžĄĚž†Ā žĄĪžßą
ŽĎėŽ†ąžôÄ ŽĄďžĚī
 žõźžĚė ŽĄďžĚīŽäĒ žÉČžĻ†Žźú ž†ēžā¨ÍįĀŪėēžĚė ŽĄďžĚīžĚė ŌÄŽįįžĚīŽč§.
žõźžĚė ŽĄďžĚīŽäĒ žÉČžĻ†Žźú ž†ēžā¨ÍįĀŪėēžĚė ŽĄďžĚīžĚė ŌÄŽįįžĚīŽč§.
 ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīÍįÄ
ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīÍįÄ  žĚł žõźžĚÄ Ž¨īŪēúŪěą žěĎžĚÄ Ž∂ÄžĪĄÍľīŽď§Ž°ú ž™ľÍįúžĖī ÍįÄŽ°ú ÍłłžĚī
žĚł žõźžĚÄ Ž¨īŪēúŪěą žěĎžĚÄ Ž∂ÄžĪĄÍľīŽď§Ž°ú ž™ľÍįúžĖī ÍįÄŽ°ú ÍłłžĚī  , žĄłŽ°ú ÍłłžĚī
, žĄłŽ°ú ÍłłžĚī  žĚė žßĀžā¨ÍįĀŪėēžúľŽ°ú ŽßĆŽď§ žąė žěąŽč§.
žĚė žßĀžā¨ÍįĀŪėēžúľŽ°ú ŽßĆŽď§ žąė žěąŽč§.
žĖīŽĖ§ žõźžĚė ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ  ŽĚľÍ≥† ŪēėÍ≥†, žßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ
ŽĚľÍ≥† ŪēėÍ≥†, žßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ  ŽĚľÍ≥† ŪēėŽ©ī, žõźžĚė ŽĎėŽ†ąŽäĒ
ŽĚľÍ≥† ŪēėŽ©ī, žõźžĚė ŽĎėŽ†ąŽäĒ

žĚīŽč§. žó¨ÍłįžĄú  ŽäĒ žõźž£ľžú®žĚīŽč§. žĚīŽäĒ žēĹ 3.1415‚ĶŽ•ľ ÍįížúľŽ°ú ŪēėŽäĒ žīąžõĒžąėžĚīŽč§.
ŽäĒ žõźž£ľžú®žĚīŽč§. žĚīŽäĒ žēĹ 3.1415‚ĶŽ•ľ ÍįížúľŽ°ú ŪēėŽäĒ žīąžõĒžąėžĚīŽč§.
žĖīŽĖ§ žõźžĚė ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ  ŽĚľÍ≥† ŪēėÍ≥†, žßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ
ŽĚľÍ≥† ŪēėÍ≥†, žßÄŽ¶ĄžĚė ÍłłžĚīŽ•ľ  ŽĚľÍ≥† ŪēėÍ≥†, ŽĎėŽ†ąŽ•ľ
ŽĚľÍ≥† ŪēėÍ≥†, ŽĎėŽ†ąŽ•ľ  ŽĚľÍ≥† ŪēėŽ©ī, žõź(žúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėē)žĚė ŽĄďžĚīŽäĒ
ŽĚľÍ≥† ŪēėŽ©ī, žõź(žúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėē)žĚė ŽĄďžĚīŽäĒ

žĚīŽč§. ŽďĪž£ľ Ž∂ÄŽďĪžčĚžóź ŽĒįŽ•īŽ©ī, žĚīŽäĒ ŽĎėŽ†ąÍįÄ  žĚł ŽčęŪěĆ Í≥°žĄ†žúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėēžĚī ÍįÄžßą žąė žěąŽäĒ žĶúŽĆÄ ŽĄďžĚīžĚīŽč§.
žĚł ŽčęŪěĆ Í≥°žĄ†žúľŽ°ú ŽĎėŽü¨žčłžĚł ŽŹĄŪėēžĚī ÍįÄžßą žąė žěąŽäĒ žĶúŽĆÄ ŽĄďžĚīžĚīŽč§.
Žį©ž†ēžčĚ
ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥Ą
 ž§Ďžč¨žĚī (2, 1)žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī 3žĚł žõź
ž§Ďžč¨žĚī (2, 1)žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī 3žĚł žõź
2žį®žõź ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥Ą žúĄžĚė ž§Ďžč¨žĚī  žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī
žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī  žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ
žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ

žĚīŽč§.[1]:22, ¬ß3 žĚīŽäĒ ŪĒľŪÉÄÍ≥†ŽĚľžä§ ž†ēŽ¶¨Ž•ľ ŪÜĶŪēī žú†ŽŹĄŽźúŽč§.
2žį®žõź ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥Ą žúĄžĚė žõźžĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚÄ

žĚīŽč§. Žč®,  ŽäĒ žč§žąėžĚīŽ©į,
ŽäĒ žč§žąėžĚīŽ©į,

žĚīžĖīžēľ ŪēúŽč§.[1]:23, ¬ß3.2 žĘĆŽ≥ÄžĚÄ ŽįėžßÄŽ¶ĄžĚė 4Žįįžóź ŽĆÄžĚĎŪēėŽ©į, '=0'žĚľ Í≤Ĺžöį ŪēúžõźžÜĆ žßĎŪē©žĚī ŽźėÍ≥†, '<0'žĚľ Í≤Ĺžöį Í≥ĶžßĎŪē©žĚī ŽźúŽč§.[1]:24, ¬ß3.2, Example 3.2
ŪŹČŽ©ī žúĄžĚė Ž™®Žď† žõźžĚÄ ž†Āž†ąŪēú ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥ĄŽ•ľ ž∑®ŪĖąžĚĄ ŽēĆ

žôÄ ÍįôžĚÄ ŪĎúž§Äž†ĀžĚł Žį©ž†ēžčĚžúľŽ°ú ŪĎúŪėĄŽźúŽč§. Žč®,  žĚīžĖīžēľ ŪēúŽč§. žĚīŽü¨Ūēú ÍľīžĚė Žį©ž†ēžč̞̥ žĖĽžúľŽ†§Ž©ī žõźžĚė ž§Ďžč¨žĚĄ žĘĆŪĎúÍ≥ĄžĚė žõźž†źžúľŽ°ú žāľÍłįŽßĆ ŪēėŽ©ī ŽźúŽč§.
žĚīžĖīžēľ ŪēúŽč§. žĚīŽü¨Ūēú ÍľīžĚė Žį©ž†ēžč̞̥ žĖĽžúľŽ†§Ž©ī žõźžĚė ž§Ďžč¨žĚĄ žĘĆŪĎúÍ≥ĄžĚė žõźž†źžúľŽ°ú žāľÍłįŽßĆ ŪēėŽ©ī ŽźúŽč§.
2žį®žõź ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥Ą žúĄžĚė ž§Ďžč¨žĚī  žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī
žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī  žĚł žõźžĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Žß§ÍįúŽ≥Äžąė Žį©ž†ēžč̞̥ ÍįĖŽäĒŽč§.[1]:23, ¬ß3.2, (3.5)
žĚł žõźžĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Žß§ÍįúŽ≥Äžąė Žį©ž†ēžč̞̥ ÍįĖŽäĒŽč§.[1]:23, ¬ß3.2, (3.5)

žó¨ÍłįžĄú  žĚÄ ÍįĀÍįĀ žĹĒžā¨žĚł Ūē®žąėžôÄ žā¨žĚł Ūē®žąėžĚīÍ≥†,
žĚÄ ÍįĀÍįĀ žĹĒžā¨žĚł Ūē®žąėžôÄ žā¨žĚł Ūē®žąėžĚīÍ≥†,  ŽäĒ Žß§Íįú Ž≥ÄžąėžĚīŽč§.
ŽäĒ Žß§Íįú Ž≥ÄžąėžĚīŽč§.
Í∑ĻžĘĆŪĎúÍ≥Ą
ŽćįžĻīŽ•īŪäł žĘĆŪĎú  ŽĆÄžč† Í∑ĻžĘĆŪĎú
ŽĆÄžč† Í∑ĻžĘĆŪĎú  Ž•ľ žā¨žö©Ūē† žąėŽŹĄ žěąŽč§. ž¶Č, Í∑ĻžĘĆŪĎúÍ≥Ą žúĄžĚė ž§Ďžč¨žĚī
Ž•ľ žā¨žö©Ūē† žąėŽŹĄ žěąŽč§. ž¶Č, Í∑ĻžĘĆŪĎúÍ≥Ą žúĄžĚė ž§Ďžč¨žĚī  žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī
žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī  žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ
žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ

žĚīŽč§.
Ž≥ĶžÜĆŪŹČŽ©ī
ŽćįžĻīŽ•īŪäł žĘĆŪĎúŽāė Í∑ĻžĘĆŪĎúŽ•ľ Ž≥ĶžÜĆžąė  Ž°ú ŽĆÄžč†ŪēėŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚė ŪÜĶžĚľŽźú Žį©ž†ēžč̞̥ žĖĽžĚĄ žąė žěąŽč§.
Ž°ú ŽĆÄžč†ŪēėŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚė ŪÜĶžĚľŽźú Žį©ž†ēžč̞̥ žĖĽžĚĄ žąė žěąŽč§.
Ž≥ĶžÜĆŪŹČŽ©ī žúĄžóźžĄú, ž§Ďžč¨žĚī  žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī
žĚīÍ≥† ŽįėžßÄŽ¶ĄžĚī  žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ
žĚł žõźžĚė Žį©ž†ēžčĚžĚÄ

žĚīŽč§. žó¨ÍłįžĄú  ŽäĒ Ž≥ĶžÜĆžąėžĚė ž†ąŽĆďÍįížĚīŽč§.
ŽäĒ Ž≥ĶžÜĆžąėžĚė ž†ąŽĆďÍįížĚīŽč§.
ŽėźŪēú Ž≥ĶžÜĆŪŹČŽ©ī žúĄžĚė žõźžĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚÄ

žĚīŽč§. žó¨ÍłįžĄú  ŽäĒ žľ§Ž†ą Ž≥ĶžÜĆžąėžĚīŽč§. Žč®,
ŽäĒ žľ§Ž†ą Ž≥ĶžÜĆžąėžĚīŽč§. Žč®,  ŽäĒ žč§žąėžĚīÍ≥†,
ŽäĒ žč§žąėžĚīÍ≥†,  ŽäĒ Ž≥ĶžÜĆžąėžĚīŽ©į,
ŽäĒ Ž≥ĶžÜĆžąėžĚīŽ©į,


žĚīžĖīžēľ ŪēúŽč§. ŽėźŪēú,  ŽĆÄžč†
ŽĆÄžč†  žĚĄ ž∑®ŪēėÍ≥† Žč§Ž•ł ž°įÍĪīžĚĄ Í∑łŽĆÄŽ°ú ŽĎźŽ©ī Ž≥ĶžÜĆŪŹČŽ©ī žúĄžĚė žßĀžĄ†žĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚĄ žĖĽŽäĒŽč§. ž¶Č,
žĚĄ ž∑®ŪēėÍ≥† Žč§Ž•ł ž°įÍĪīžĚĄ Í∑łŽĆÄŽ°ú ŽĎźŽ©ī Ž≥ĶžÜĆŪŹČŽ©ī žúĄžĚė žßĀžĄ†žĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚĄ žĖĽŽäĒŽč§. ž¶Č,  žĚīŽĚľŽäĒ ž°įÍĪīžĚĄ ž†úÍĪįŪēėÍ≥† Žč§Ž•ł ž°įÍĪīžĚĄ Í∑łŽĆÄŽ°ú ŽĎźŽ©ī žĚľŽįėŪôĒ žõźžĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚĄ žĖĽŽäĒŽč§.
žĚīŽĚľŽäĒ ž°įÍĪīžĚĄ ž†úÍĪįŪēėÍ≥† Žč§Ž•ł ž°įÍĪīžĚĄ Í∑łŽĆÄŽ°ú ŽĎźŽ©ī žĚľŽįėŪôĒ žõźžĚė Žį©ž†ēžčĚžĚė žĚľŽįėž†ĀžĚł ÍľīžĚĄ žĖĽŽäĒŽč§.
ž†ĎžĄ†žĚė Žį©ž†ēžčĚ
2žį®žõź ŽćįžĻīŽ•īŪäł žĘĆŪĎúÍ≥Ą žúĄžóźžĄú, žõź

žĚė  žĚĄ ž†Ďž†źžúľŽ°ú ŪēėŽäĒ ž†ĎžĄ†žĚė Žį©ž†ēžčĚžĚÄ
žĚĄ ž†Ďž†źžúľŽ°ú ŪēėŽäĒ ž†ĎžĄ†žĚė Žį©ž†ēžčĚžĚÄ

žĚīŽč§.
žõź

žĚė ÍłįžöłÍłįÍįÄ  žĚł ž†ĎžĄ†žĚė Žį©ž†ēžčĚžĚÄ
žĚł ž†ĎžĄ†žĚė Žį©ž†ēžčĚžĚÄ

žĚīŽč§.
ÍłįŪēėž†Ā žĄĪžßą
ŽĆÄžĻ≠
- žõźžĚÄ žßÄŽ¶Ąžóź ŽĆÄŪēú Žįėžā¨žôÄ žõźžĚė ž§Ďžč¨žóź ŽĆÄŪēú ŪöĆž†Ąžóź ŽĆÄŪēėžó¨ ŽĆÄžĻ≠žĚīŽč§.[2]:227, ¬ß20.1, Theorem 20.3
- ž¶Č, žõźžĚė ŽĆÄžĻ≠ÍĶįžĚÄ 2žį®žõź žßĀÍĶźÍĶį
 žĚīŽč§.
žĚīŽč§.
- žěĄžĚėžĚė ŽĎź žõźžĚÄ žĄúŽ°ú ž§Ďžč¨ ŽčģžĚĆžĚīŽ©į, ŽŹôžč¨žõźžĚī žēĄŽčź Í≤Ĺžöį ŽĎź žõźžĚė ž§Ďžč¨žĚĄ žěáŽäĒ žĄ†Ž∂ĄžĚė ŽįėžßÄŽ¶ĄžĚė ŽĻĄžóź ŽĒįŽ•ł ŽāīŽ∂Ąž†ź ŽįŹ žôłŽ∂Ąž†źžĚĄ ŽčģžĚĆ ž§Ďžč¨žúľŽ°ú ÍįĖŽäĒŽč§.[3]:19, ¬ß25
- ŽįėžßÄŽ¶ĄžĚė ÍłłžĚīÍįÄ ÍįôžĚÄ Ž™®Žď† žõźžĚÄ žĄúŽ°ú Ūē©ŽŹôžĚīŽč§.[4]:23, ¬ß1F
- Í≥ĶžĄ†ž†źžĚī žēĄŽčĆ žĄł ž†źžĚĄ žßÄŽāėŽäĒ žõźžĚÄ Ūē≠žÉĀ žú†žĚľŪēėÍ≤Ć ž°īžě¨ŪēúŽč§.[4]:23, ¬ß1F, Theorem 1.15
ŪėłžôÄ ŪėĄ
- ŪėĄžĚė žąėžßĀ žĚīŽďĪŽ∂ĄžĄ†žĚÄ žõźžĚė ž§Ďžč¨žĚĄ žßÄŽāúŽč§.[2]:227, ¬ß20.1, Theorem 20.2
- ž¶Č, ŪėĄžóź žąėžßĀžĚł žßÄŽ¶ĄžĚÄ ŪėĄžĚĄ žĚīŽďĪŽ∂ĄŪēúŽč§.[2]:227, ¬ß20.1, Theorem 20.2
- ž¶Č, žßÄŽ¶ĄžĚī žēĄŽčĆ ŪėĄžĚĄ žĚīŽďĪŽ∂ĄŪēėŽäĒ žßÄŽ¶ĄžĚÄ ŪėĄžóź žąėžßĀžĚīŽč§.[2]:227, ¬ß20.1, Theorem 20.2
- žßÄŽ¶ĄžĚÄ žõźžĚė ÍįÄžě• Íłī ŪėĄžĚīŽč§.[4]:23, ¬ß1F
- (Žį©Ž©Ī ž†ēŽ¶¨) žõź žúĄžóź žěąžßÄ žēäžĚÄ ž†ź
 Ž•ľ žßÄŽāėŽäĒ ŽĎź žßĀžĄ† ÍįÄžöīŽćį ŪēėŽāėŽäĒ žõźÍ≥ľ ž†ź
Ž•ľ žßÄŽāėŽäĒ ŽĎź žßĀžĄ† ÍįÄžöīŽćį ŪēėŽāėŽäĒ žõźÍ≥ľ ž†ź  žôÄ
žôÄ  žóźžĄú ŽßĆŽāėÍ≥†, Žč§Ž•ł ŪēėŽāėŽäĒ žõźÍ≥ľ ž†ź
žóźžĄú ŽßĆŽāėÍ≥†, Žč§Ž•ł ŪēėŽāėŽäĒ žõźÍ≥ľ ž†ź  žôÄ
žôÄ  žóźžĄú ŽßĆŽāúŽč§Í≥† ŪēėŽ©ī,
žóźžĄú ŽßĆŽāúŽč§Í≥† ŪēėŽ©ī,  žĚīŽč§.[4]:47, ¬ß1H, Theorem 1.35
žĚīŽč§.[4]:47, ¬ß1H, Theorem 1.35
- žõź žúĄžĚė ž†źÍ≥ľ ŪėĄ žā¨žĚīžĚė ÍĪįŽ¶¨žôÄ žßÄŽ¶ĄžĚė Í≥ĪžĚÄ ž†źÍ≥ľ ŪėĄžĚė žĖĎ ŽĀĚž†ź žā¨žĚīžĚė ÍĪįŽ¶¨žĚė Í≥ĪÍ≥ľ ÍįôŽč§.[3]:71, ¬ß101
žõźÍ≥ľ žßĀžĄ†žĚė žúĄžĻė ÍīÄÍ≥Ą
ŪŹČŽ©ī žúĄžĚė žõźÍ≥ľ žßĀžĄ†žĚė žúĄžĻė ÍīÄÍ≥ĄŽäĒ žõźžĚė ž§Ďžč¨žóźžĄú žßĀžĄ†ÍĻĆžßÄžĚė ÍĪįŽ¶¨  žôÄ žõźžĚė ŽįėžßÄŽ¶Ą
žôÄ žõźžĚė ŽįėžßÄŽ¶Ą  žĚė ŽĆÄžÜĆ ÍīÄÍ≥Ąžóź ŽĒįŽĚľ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Í≤ĹžöįŽ°ú ŽāėŽČúŽč§.
žĚė ŽĆÄžÜĆ ÍīÄÍ≥Ąžóź ŽĒįŽĚľ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Í≤ĹžöįŽ°ú ŽāėŽČúŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ ŽßĆŽāėžßÄ žēäŽäĒŽč§.
ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ ŽßĆŽāėžßÄ žēäŽäĒŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ Ūēú ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, žßĀžĄ†žĚÄ žõźžĚė ž†ĎžĄ†žĚīŽč§.
ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ Ūēú ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, žßĀžĄ†žĚÄ žõźžĚė ž†ĎžĄ†žĚīŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ ŽĎź ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, žßĀžĄ†žĚÄ žõźžĚė Ūē†žĄ†žĚīŽč§.
ŽĚľŽ©ī, žõźÍ≥ľ žßĀžĄ†žĚÄ ŽĎź ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, žßĀžĄ†žĚÄ žõźžĚė Ūē†žĄ†žĚīŽč§.
ŽĎź žõźžĚė žúĄžĻė ÍīÄÍ≥Ą
ŽĎź žõźžĚė žúĄžĻė ÍīÄÍ≥ĄŽäĒ ŽĎź žõźžĚė ŽįėžßÄŽ¶Ą  žôÄ ŽĎź ž§Ďžč¨ žā¨žĚīžĚė ÍĪįŽ¶¨
žôÄ ŽĎź ž§Ďžč¨ žā¨žĚīžĚė ÍĪįŽ¶¨  žóź ŽĒįŽĚľ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Í≤ĹžöįŽ°ú ŽāėŽČúŽč§.
žóź ŽĒįŽĚľ Žč§žĚĆÍ≥ľ ÍįôžĚÄ Í≤ĹžöįŽ°ú ŽāėŽČúŽč§.
- ŽßĆžēĹ
 žĚīÍĪįŽāė
žĚīÍĪįŽāė  ŽĚľŽ©ī, ŽĎź žõźžĚÄ ŽßĆŽāėžßÄ žēäŽäĒŽč§.
ŽĚľŽ©ī, ŽĎź žõźžĚÄ ŽßĆŽāėžßÄ žēäŽäĒŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, ŽĎź žõźžĚÄ žĄúŽ°úžĚė žôłŽ∂Äžóź ŽÜďžĚīŽ©į, ÍĶźž†źžĚĄ ÍįÄžßÄžßÄ žēäŽäĒŽč§.
ŽĚľŽ©ī, ŽĎź žõźžĚÄ žĄúŽ°úžĚė žôłŽ∂Äžóź ŽÜďžĚīŽ©į, ÍĶźž†źžĚĄ ÍįÄžßÄžßÄ žēäŽäĒŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, žěĎžĚÄ žõźžĚÄ ŪĀį žõźžĚė ŽāīŽ∂Äžóź ŽÜďžĚīŽ©į, ÍĶźž†źžĚĄ ÍįÄžßÄžßÄ žēäŽäĒŽč§.
ŽĚľŽ©ī, žěĎžĚÄ žõźžĚÄ ŪĀį žõźžĚė ŽāīŽ∂Äžóź ŽÜďžĚīŽ©į, ÍĶźž†źžĚĄ ÍįÄžßÄžßÄ žēäŽäĒŽč§.
- ŽßĆžēĹ
 žĚīÍĪįŽāė
žĚīÍĪįŽāė  ŽĚľŽ©ī, ŽĎź žõźžĚÄ Ūēú ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, ŽĎź žõźžĚÄ žĄúŽ°ú ž†ĎŪēúŽč§.
ŽĚľŽ©ī, ŽĎź žõźžĚÄ Ūēú ž†źžóźžĄú ŽßĆŽāúŽč§. ž¶Č, ŽĎź žõźžĚÄ žĄúŽ°ú ž†ĎŪēúŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, ŽĎź žõźžĚÄ žĄúŽ°úžĚė žôłŽ∂Ğ󟞥ú ž†ĎŪēúŽč§. ž¶Č, ŽĎź žõźžĚÄ žôłž†ĎŪēúŽč§.
ŽĚľŽ©ī, ŽĎź žõźžĚÄ žĄúŽ°úžĚė žôłŽ∂Ğ󟞥ú ž†ĎŪēúŽč§. ž¶Č, ŽĎź žõźžĚÄ žôłž†ĎŪēúŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, žěĎžĚÄ žõźžĚī ŪĀį žõźžĚė ŽāīŽ∂Ğ󟞥ú ŪĀį žõźžóź ž†ĎŪēúŽč§. ž¶Č, ŽĎź žõźžĚÄ Žāīž†ĎŪēúŽč§.
ŽĚľŽ©ī, žěĎžĚÄ žõźžĚī ŪĀį žõźžĚė ŽāīŽ∂Ğ󟞥ú ŪĀį žõźžóź ž†ĎŪēúŽč§. ž¶Č, ŽĎź žõźžĚÄ Žāīž†ĎŪēúŽč§.
- ŽßĆžēĹ
 ŽĚľŽ©ī, ŽĎź žõźžĚÄ ŽĎź ž†źžóźžĄú ŽßĆŽāúŽč§.
ŽĚľŽ©ī, ŽĎź žõźžĚÄ ŽĎź ž†źžóźžĄú ŽßĆŽāúŽč§.
ž§Ďžč¨ÍįĀÍ≥ľ žõźž£ľÍįĀ
- ž£ľžĖīžßĄ Ūėłžóź ŽĆÄŪēú žõźž£ľÍįĀžĚė ŪĀ¨ÍłįŽäĒ Í∑ł Ūėłžóź ŽĆÄŪēú ž§Ďžč¨ÍįĀžĚė 1/2žĚīŽč§.[4]:25, ¬ß1F, Theorem 1.16
- ÍįôžĚÄ Ūėłžóź ŽĆÄŪēú ŽĎź žõźž£ľÍįĀžĚė ŪĀ¨ÍłįŽäĒ žĄúŽ°ú ÍįôŽč§.[4]:25, ¬ß1F
- žľ§Ž†ąŪėłžóź ŽĆÄŪēú ŽĎź ž§Ďžč¨ÍįĀžĚÄ žĄúŽ°ú Ž≥īÍįĀžĚīŽč§.
- (ŪÉąŽ†ąžä§ ž†ēŽ¶¨) žßÄŽ¶Ąžóź ŽĆÄŪēú žõźž£ľÍįĀžĚÄ žßĀÍįĀžĚīŽč§.
- žõźžĚė ŽĎź ŪėĄžĚī žõź ŽāīŽ∂Ğ󟞥ú žĚīŽ£®ŽäĒ ÍįĀžĚė ŪĀ¨ÍłįŽäĒ žĚī ÍįĀÍ≥ľ ŽßěÍľ≠žßÄÍįĀžĚė ŽāīŽ∂Äžóź ŪŹ¨Ūē®ŽźėŽäĒ ŽĎź Ūėłžóź ŽĆÄŪēú ž§Ďžč¨ÍįĀžĚė Ūē©žĚė 1/2žĚīŽč§.[4]:27, ¬ß1F, Corollary 1.19
- žõźžĚė ŽĎź Ūē†žĄ†žĚī žõź žôłŽ∂Ğ󟞥ú žĚīŽ£®ŽäĒ ÍįĀžĚė ŪĀ¨ÍłįŽäĒ žĚī ÍįĀžĚė ŽāīŽ∂Äžóź ŪŹ¨Ūē®ŽźėŽäĒ ŽĎź Ūėłžóź ŽĆÄŪēú ž§Ďžč¨ÍįĀžĚė žį®žĚė 1/2žĚīŽč§.[4]:27, ¬ß1F, Corollary 1.18
ž†ĎžĄ†
- žõź žúĄžĚė Ūēú ž†źžĚĄ žßÄŽāėŽäĒ žõźžĚė ž†ĎžĄ†žĚÄ žú†žĚľŪēėÍ≤Ć ž°īžě¨ŪēėÍ≥†, žĚīŽäĒ žĚī ž†źžĚĄ žßÄŽāėŽäĒ ŽįėžßÄŽ¶Ąžóź žąėžßĀžĚīŽč§.[2]:228, ¬ß20.1, Theorem 20.4[4]:30-31, ¬ß1F
- ž¶Č, ŽįėžßÄŽ¶ĄžĚė ŽįėžßÄŽ¶Ą ŽĀĚž†źžóźžĄúžĚė žąėžĄ†žĚÄ žõźžóź ž†ĎŪēúŽč§.[2]:228, ¬ß20.1, Theorem 20.4
- ž¶Č, žõźžĚė ž†ĎžĄ†žĚė ž†Ďž†źžóźžĄúžĚė žąėžĄ†žĚÄ žõźžĚė ž§Ďžč¨žĚĄ žßÄŽāúŽč§.
- žõź žôłŽ∂ÄžĚė Ūēú ž†źžĚĄ žßÄŽāėŽäĒ žõźžĚė ž†ĎžĄ†žĚÄ ž†ēŪôēŪěą 2ÍįúžĚīÍ≥†, žĚī ž†źÍ≥ľ ŽĎź ž†Ďž†ź žā¨žĚīžĚė ÍĪįŽ¶¨ŽäĒ ÍįôžúľŽ©į, ŽĎź ž†ĎžĄ†žĚī žĚīŽ£®ŽäĒ ÍįĀÍ≥ľ ŽĎź ž†Ďž†źžĚĄ žßÄŽāėŽäĒ ŽįėžßÄŽ¶ĄžĚī žĚīŽ£®ŽäĒ ÍįĀžĚÄ žĄúŽ°ú Ž≥īÍįĀžĚīŽč§.
- žõźžĚė ž†ĎŪėĄÍįĀžĚė ŪĀ¨ÍłįŽäĒ ŪėĄžĚĄ Íłįž§ÄžúľŽ°ú žĚīžôÄ ÍįôžĚÄ ž™Ĺžóź žěąŽäĒ Ūėłžóź ŽĆÄŪēú ž§Ďžč¨ÍįĀžĚė 1/2žĚīŽč§.[4]:31, ¬ß1F, Theorem 1.23
- žõźžĚė ž†ĎžĄ†Í≥ľ Ūē†žĄ†žĚī žõź žôłŽ∂Ğ󟞥ú žĚīŽ£®ŽäĒ ÍįĀžĚÄ ÍįĀžĚė ŽāīŽ∂Äžóź ŪŹ¨Ūē®Žźú ŽĎź ŪėłžĚė ž§Ďžč¨ÍįĀžĚė žį®žĚė 1/2žĚīŽč§.[4]:31, ¬ß1F, Corollary 1.24
- žôłž†ĎŪēėŽäĒ ŽĎź žõźžĚė ÍĶźž†źžĚĄ žßÄŽāėŽäĒ ŽĎź Í≥ĶŪÜĶ Ūē†žĄ† žā¨žĚīžĚė ŽĎź ŪėĄžĚÄ žĄúŽ°ú ŪŹČŪĖČŪēúŽč§.[4]:31, ¬ß1F, Problem 1.25
- (ž†ĎžĄ†žóź ŽĆÄŪēú Žį©Ž©Ī ž†ēŽ¶¨)žõź žôłŽ∂ÄžĚė ž†ź
 Ž•ľ žßÄŽāėŽäĒ ŽĎź žßĀžĄ† ÍįÄžöīŽćį ŪēėŽāėŽäĒ žõźÍ≥ľ
Ž•ľ žßÄŽāėŽäĒ ŽĎź žßĀžĄ† ÍįÄžöīŽćį ŪēėŽāėŽäĒ žõźÍ≥ľ  žôÄ
žôÄ  žóźžĄú ŽßĆŽāėÍ≥†, ŪēėŽāėŽäĒ žõźžóź ž†ź
žóźžĄú ŽßĆŽāėÍ≥†, ŪēėŽāėŽäĒ žõźžóź ž†ź  žóźžĄú ž†ĎŪēúŽč§Í≥† ŪēėŽ©ī,
žóźžĄú ž†ĎŪēúŽč§Í≥† ŪēėŽ©ī,  žĚīŽč§.
žĚīŽč§.
žõźžĚė žßĀÍĶź
- ŽĎź žõźžĚė ÍĶźž†źžóźžĄúžĚė ŽĎź ž†ĎžĄ†žĚī žĄúŽ°ú žąėžßĀžĚľ Í≤Ĺžöį ŽĎź žõźžĚī žĄúŽ°ú žßĀÍĶźŪēúŽč§Í≥† ŪēúŽč§.[3]:33, ¬ß48
- ŽĎź žõźžĚė ŽįėžßÄŽ¶ĄžĚī
 žĚīÍ≥†, ŽĎź ž§Ďžč¨ žā¨žĚīžĚė ÍĪįŽ¶¨ÍįÄ
žĚīÍ≥†, ŽĎź ž§Ďžč¨ žā¨žĚīžĚė ÍĪįŽ¶¨ÍįÄ  ŽĚľÍ≥† Ūē† ŽēĆ, ŽĎź žõźžĚī žĄúŽ°ú žßĀÍĶźŪē† ŪēĄžöĒž∂©Ž∂Ąž°įÍĪīžĚÄ
ŽĚľÍ≥† Ūē† ŽēĆ, ŽĎź žõźžĚī žĄúŽ°ú žßĀÍĶźŪē† ŪēĄžöĒž∂©Ž∂Ąž°įÍĪīžĚÄ  žĚīŽč§.[3]:34, ¬ß48
žĚīŽč§.[3]:34, ¬ß48
- ž£ľžĖīžßĄ žõźžóź žßĀÍĶźŪēėÍ≥† ž§Ďžč¨žĚī žõź žôłŽ∂ÄžĚė ž£ľžĖīžßĄ ž†źžĚł žõźžĚÄ žú†žĚľŪēėÍ≤Ć ž°īžě¨ŪēúŽč§.[3]:34, ¬ß48
- ž£ľžĖīžßĄ žõźžóź žßĀÍĶźŪēėÍ≥† žõźžĚė žßÄŽ¶ĄžĚī žēĄŽčĆ ŪėĄžĚė ŽĎź ŽĀĚž†źžĚĄ žßÄŽāėŽäĒ žõźžĚÄ žú†žĚľŪēėÍ≤Ć ž°īžě¨ŪēúŽč§.[3]:34, ¬ß48
žěĎŽŹĄ
Í≥ĶžĄ†ž†źžĚī žēĄŽčĆ žĄł ž†źžĚĄ žßÄŽāėŽäĒ žõź
Í≥ĶžĄ†ž†źžĚī žēĄŽčĆ žĄł ž†ź  Ž•ľ žßÄŽāėŽäĒ žõźžĚÄ žĽīŪ澞䧞ôÄ žěźŽ•ľ žā¨žö©Ūēėžó¨ Žč§žĚĆÍ≥ľ ÍįôžĚī žěĎŽŹĄŪē† žąė žěąŽč§.
Ž•ľ žßÄŽāėŽäĒ žõźžĚÄ žĽīŪ澞䧞ôÄ žěźŽ•ľ žā¨žö©Ūēėžó¨ Žč§žĚĆÍ≥ľ ÍįôžĚī žěĎŽŹĄŪē† žąė žěąŽč§.
- žĄ†Ž∂Ą
 žĚė žąėžßĀ žĚīŽďĪŽ∂ĄžĄ†žĚĄ Í∑łŽ¶įŽč§.
žĚė žąėžßĀ žĚīŽďĪŽ∂ĄžĄ†žĚĄ Í∑łŽ¶įŽč§.
- žĄ†Ž∂Ą
 žĚė žąėžßĀ žĚīŽďĪŽ∂ĄžĄ†žĚĄ Í∑łŽ¶įŽč§.
žĚė žąėžßĀ žĚīŽďĪŽ∂ĄžĄ†žĚĄ Í∑łŽ¶įŽč§.
- žĄ†Ž∂Ą
 žôÄ
žôÄ  žĚė ÍĶźž†ź
žĚė ÍĶźž†ź  Ž•ľ ž∑®ŪēúŽč§.
Ž•ľ ž∑®ŪēúŽč§.
- ž†ź
 Ž•ľ ž§Ďžč¨žúľŽ°ú ŪēėÍ≥† žĄ†Ž∂Ą
Ž•ľ ž§Ďžč¨žúľŽ°ú ŪēėÍ≥† žĄ†Ž∂Ą  Ž•ľ ŽįėžßÄŽ¶ĄžúľŽ°ú ŪēėŽäĒ žõźžĚĄ Í∑łŽ¶įŽč§. žĚī Í≤Ĺžöį žõźžĚÄ ž†ź
Ž•ľ ŽįėžßÄŽ¶ĄžúľŽ°ú ŪēėŽäĒ žõźžĚĄ Í∑łŽ¶įŽč§. žĚī Í≤Ĺžöį žõźžĚÄ ž†ź  Ž•ľ žßÄŽāúŽč§.
Ž•ľ žßÄŽāúŽč§.
žõźžĚė ž§Ďžč¨
ž£ľžĖīžßĄ žõźžĚė ž§Ďžč¨žĚÄ žĽīŪ澞䧞ôÄ žěźŽ•ľ žā¨žö©Ūēėžó¨ Žč§žĚĆÍ≥ľ ÍįôžĚī žěĎŽŹĄŪē† žąė žěąŽč§.
- žõź žúĄžĚė ŽĎź ž†ź
 žĚĄ ž∑®ŪēúŽč§.
žĚĄ ž∑®ŪēúŽč§.
- žĄ†Ž∂Ą
 žĚė ž†ź
žĚė ž†ź  žóźžĄúžĚė žąėžĄ†
žóźžĄúžĚė žąėžĄ†  Ž•ľ Í∑łŽ¶įŽč§.
Ž•ľ Í∑łŽ¶įŽč§.
- žßĀžĄ†
 žôÄ žõźžĚė ÍĶźž†ź
žôÄ žõźžĚė ÍĶźž†ź  Ž•ľ ž∑®ŪēúŽč§. žĚī Í≤Ĺžöį žĄ†Ž∂Ą
Ž•ľ ž∑®ŪēúŽč§. žĚī Í≤Ĺžöį žĄ†Ž∂Ą  ŽäĒ žõźžĚė žßÄŽ¶ĄžĚīŽč§.
ŽäĒ žõźžĚė žßÄŽ¶ĄžĚīŽč§.
- Žėź Žč§Ž•ł žßÄŽ¶Ą
 žĚĄ žěĎŽŹĄŪēúŽč§.
žĚĄ žěĎŽŹĄŪēúŽč§.
- žĄ†Ž∂Ą
 žôÄ
žôÄ  žĚė ÍĶźž†ź
žĚė ÍĶźž†ź  Ž•ľ ž∑®ŪēúŽč§. žĚī Í≤Ĺžöį ž†ź
Ž•ľ ž∑®ŪēúŽč§. žĚī Í≤Ĺžöį ž†ź  ŽäĒ žõźžĚė ž§Ďžč¨žĚīŽč§.
ŽäĒ žõźžĚė ž§Ďžč¨žĚīŽč§.
žõźž†Ā Ž¨łž†ú
žõźž†Ā Ž¨łž†úŽäĒ ž£ľžĖīžßĄ žõźÍ≥ľ ŽĄďžĚīÍįÄ ÍįôžĚÄ ž†ēžā¨ÍįĀŪėēžĚĄ žĽīŪ澞䧞ôÄ žěźŽ°ú žěĎŽŹĄŪēėŽäĒ Ž¨łž†úŽ•ľ žĚľžĽęŽäĒŽč§. žĚīŽäĒ žõźž£ľžú®  ÍįÄ žīąžõĒžąėžĚīŽĮÄŽ°ú Ž∂ąÍįÄŽä•ŪēėŽč§.
ÍįÄ žīąžõĒžąėžĚīŽĮÄŽ°ú Ž∂ąÍįÄŽä•ŪēėŽč§.
ÍłįŪÉÄ ÍīÄŽ†® ž£ľž†ú
Žāīž†Ďžõź, žôłž†Ďžõź, Žį©ž†Ďžõź
Ž™®Žď† žāľÍįĀŪėēžĚÄ žú†žĚľŪēú Žāīž†Ďžõź ŽįŹ žôłž†ĎžõźÍ≥ľ ž†ēŪôēŪěą 3ÍįúžĚė Žį©ž†ĎžõźžĚĄ ÍįĖŽäĒŽč§. Í∑łŽü¨Žāė, žĚľŽįėž†ĀžúľŽ°ú Žč§ÍįĀŪėēžĚÄ Žāīž†ĎžõźžĚīŽāė žôłž†ĎžõźžĚĄ ÍįÄžßą ŪēĄžöĒÍįÄ žóÜŽč§. žĖīŽĖ§ Žč§ÍįĀŪėēžĚī Ž™®Žď† Ž≥Äžóź ž†ĎŪēėŽäĒ žõźžĚĄ ÍįÄžßą Í≤Ĺžöį, žĚī Žč§ÍįĀŪėēžĚĄ žôłž†Ď Žč§ÍįĀŪėēžĚīŽĚľÍ≥† ŪēúŽč§. žĖīŽĖ§ Žč§ÍįĀŪėēžĚī Ž™®Žď† Íľ≠žßźžĚĄ žßÄŽāėŽäĒ žõźžĚĄ ÍįÄžßą Í≤Ĺžöį, žĚī Žč§ÍįĀŪėēžĚĄ Žāīž†Ď Žč§ÍįĀŪėēžĚīŽĚľÍ≥† ŪēúŽč§. ŽŹôžčúžóź žôłž†Ď Žč§ÍįĀŪėēžĚīŽ©į Žāīž†Ď Žč§ÍįĀŪėēžĚł Žč§ÍįĀŪėēžĚĄ žĚīž§Ďž§Ďžč¨ Žč§ÍįĀŪėēžĚīŽĚľÍ≥† ŪēúŽč§. žėąŽ•ľ Žď§žĖī, Ž™®Žď† žāľÍįĀŪėēÍ≥ľ Ž™®Žď† ž†ēŽč§ÍįĀŪėēžĚÄ žĚīž§Ďž§Ďžč¨ Žč§ÍįĀŪėēžĚīŽč§.
ž£ľžĖīžßĄ žõźžĚė Žāīž†Ď  ÍįĀŪėē ÍįÄžöīŽćį ŽĄďžĚīÍįÄ ÍįÄžě• ŪĀį Í≤ÉžĚÄ ž†ē
ÍįĀŪėē ÍįÄžöīŽćį ŽĄďžĚīÍįÄ ÍįÄžě• ŪĀį Í≤ÉžĚÄ ž†ē ÍįĀŪėēžĚīŽč§.[4]:35, ¬ß1G
ÍįĀŪėēžĚīŽč§.[4]:35, ¬ß1G
Ž¨łŪēô
- žóźŽďúžúą A. žē†Ž≥īŪäłžĚė Í≥ĶžÉĀ žąėŪēô žÜĆžĄ§ „ÄäŪĒĆŽěęŽěúŽďú„ÄčžóźžĄúŽäĒ žõźžĚī žĄĪžßĀžěźŽ°ú ž∂úŪėĄŪēėŽ©į, ŪŹČŽ©īŽŹĄŪėēŽď§ ž§Ď ÍįÄžě• Í≥†Í∑ÄŪēú Í≥ĄÍłČžúľŽ°ú žó¨Í≤®žßĄŽč§.
ÍįôžĚī Ž≥īÍłį
ÍįĀž£ľ
žôłŽ∂Ä ŽßĀŪĀ¨
 žúĄŪā§ŽĮłŽĒĒžĖī Í≥Ķžö©žóź žõź ÍīÄŽ†® ŽĮłŽĒĒžĖī Ž∂ĄŽ•ėÍįÄ žěąžäĶŽčąŽč§.
žúĄŪā§ŽĮłŽĒĒžĖī Í≥Ķžö©žóź žõź ÍīÄŽ†® ŽĮłŽĒĒžĖī Ž∂ĄŽ•ėÍįÄ žěąžäĶŽčąŽč§.