기하학에서 이심률(離心率, 영어: eccentricity)은 원뿔 곡선의 특성을 나타내는 값이다. 원뿔 곡선이 원에서 벗어나는 정도를 나타낸다고 볼 수 있다.
정의
![]() plane section of a con
plane section of a con
원뿔곡선은 점(초점)과 선(준선)까지의 거리가 일정한 비율에 있는 점의 자취로 정의할 수 있다.
이 비율을 이심률이라고 하며 일반적으로 e로 표기한다. 또한 이중원뿔을 평면으로 잘랐을 때 생기는 곡선에서 이심률은
 이고
이고- 여기서 α는 원뿔의 모선과 밑면의 사잇각이며 β는 자르는 평면과 밑면의 사잇각이다.
- 단면은 β=0일 때 원, β=α일 때 포물선이 된다. (단, 평면은 원뿔의 꼭짓점과 만나지 않아야 한다.)
- c (또는 f, e)로 표기하는 타원이나 쌍곡선의 선형 이심률은 중심과 어느 한 초점 사이의 거리이다.
- 이심률은 반장축에 대한 선형 이심률의 비율로 정의할 수 있다. 즉,
 (단, 중심이 없으면 포물선에 대한 선형 이심률이 정의되지 않는다.)
(단, 중심이 없으면 포물선에 대한 선형 이심률이 정의되지 않는다.)
성질
원뿔 곡선의 이심률의 가능한 범위는 다음과 같다. 여기서 직선 역시 이차곡선 중 일차직선이기에 정의될 수 있다.
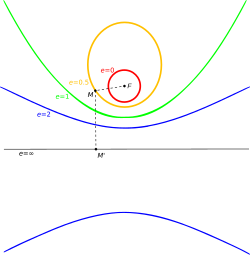 이심률이 증가하는 순서대로 늘어놓은 원뿔 곡선. 이심률이 늘어나면 곡률은 줄어든다는 점과 겹치는 곡선이 없다는 점을 주목하라.
이심률이 증가하는 순서대로 늘어놓은 원뿔 곡선. 이심률이 늘어나면 곡률은 줄어든다는 점과 겹치는 곡선이 없다는 점을 주목하라.
- 원의 이심률은 0이다.
- 타원의 이심률은 0과 1 사이의 값이다.
- 포물선의 이심률은 1이다.
- 쌍곡선의 이심률은 1보다 크다.
- 직선의 이심률은 무한대이다.
두 원뿔 곡선의 이심률이 같다는 것은 두 원뿔 곡선이 서로 닮는다는 것과 동치이다.
| 원뿔 단면
|
방정식
|
이심률 ( e )
|
선형 이심률( c )
|
| 원
|

|
0
|
0
|
| 타원
|
 또는 또는  (단, a>b) (단, a>b)
|

|

|
| 포물선
|

|
1
|
–
|
| 쌍곡선
|
 또는 또는 
|

|

|
여기서 타원과 쌍곡선의 경우 a 는 긴반지름의 길이이고 b 는 짧은반지름의 길이이다.
 의 꼴로 원뿔곡선이 주어졌을 때,
의 꼴로 원뿔곡선이 주어졌을 때,
이심률  이고,
이고,
 의 3x3 행렬의 행렬식 값이 음수이면
의 3x3 행렬의 행렬식 값이 음수이면  ,
,
양수이면  이다.
이다.
같이 보기
외부 링크