„āī„ÉÉ„Éą„É≠„Éľ„Éó„ÉĽ„Éē„ɨ„Éľ„ā≤
|
Read other articles:

Andrew Birrell (setelah Henry Fuseli), Caractacus di Tribunal Claudius di Roma (1792) Tribunal adalah sembarang orang atau pranata dengan kewenangan menghakimi, meninjau bukti-bukti, kesaksian, dan argumen untuk menentukan klaim atau sengketa‚ÄĒapakah ia disebut sebuah tribunal dalam judulnya, atau bukan.[1] Contohnya, keadaan advokat hadir di depan pengadilan dengan hakim tunggal yang bersidang dapat menjelaskan bahwa hakim tersebut adalah 'tribunal mereka'. Banyak lembaga pemerintah...

1990 treaty returning full sovereignty to Germany Final Settlement redirects here. For the Nazi plan, see Final Solution. For generic uses, see Settlement (litigation). Treaty on the Final Settlement with Respect to GermanyDrafted13 February 1990Signed12 September 1990LocationMoscow, Russian SFSR, Soviet UnionEffective15 March 1991Signatories Hans-Dietrich Genscher Lothar de Maizière Roland Dumas Eduard Shevardnadze Douglas Hurd James Baker Parties Federal Republic of Germany German Democrat...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article peut contenir un travail inédit ou des déclarations non vérifiées (avril 2020). Vous pouvez aider en ajoutant des références ou en supprimant le contenu inédit. Voir la page de discussion pour plus de détails. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (avril 2020). Si vous disposez d'ouvrages ou d'articles ...

Village in North Yorkshire, England Human settlement in EnglandBarton HillRoad junction in Barton HillBarton HillLocation within North YorkshireOS grid referenceSE707644Unitary authorityNorth YorkshireCeremonial countyNorth YorkshireRegionYorkshire and the HumberCountryEnglandSovereign stateUnited KingdomPost townYORKPostcode districtYO60PoliceNorth YorkshireFireNorth YorkshireAmbulanceYorkshire List of places UK England Yorkshire 54¬į04‚Ä≤17‚Ä≥N 0¬į55‚Ä≤12‚Ä≥W&#...

Bilateral relationsBarbadian-French relations Barbados France Barbadian-French relations are the bilateral relations between the two countries, Barbados and France. Both countries have established diplomatic relations on May 3, 1968. Barbados is represented in France through its embassy in Brussels (Belgium). France is represented in Barbados through its embassy in Castries (Saint Lucia), led by and an additional honorary consulate in Bridgetown. Bilateral relations The bilateral relations an...

State electoral district of Queensland, Australia Ferny GroveQueensland‚ÄĒLegislative AssemblyMap of the electoral district of Ferny Grove, 2017StateQueenslandMPMark FurnerPartyLaborNamesakeFerny GroveElectors36,224 (2020)Area49 km2 (18.9 sq mi)DemographicOuter-metropolitanCoordinates27¬į21‚Ä≤S 152¬į51‚Ä≤E / 27.350¬įS 152.850¬įE / -27.350; 152.850 Electorates around Ferny Grove: Pine Rivers Everton Everton Pine Rivers Ferny Grove Everton Cooper Coop...

Football league seasonSerie CSeason2018‚Äď19Dates16 September 2018 ‚Äď15 June 2019ChampionsVirtus EntellaPordenoneJuve StabiaPromotedVirtus EntellaPisaPordenoneJuve StabiaTrapaniRelegatedArzachena (bankruptcy)Albissola (bankruptcy)Cuneo (bankruptcy)Lucchese (bankruptcy)Pro Piacenza (bankruptcy)Siracusa (bankruptcy)Matera (bankruptcy)Matches played1,128Goals scored2,477 (2.2 per match)Top goalscorerPablo Granoche(20 goals)[1][2][3]Biggest home winVibonese 5‚Äď0 Vir...

British Thoroughbred racehorse SmolenskoSmolensko by John Nott Sartorius, c. 1813.SireSorcererGrandsireTrumpatorDamWowskiDamsireMentorSexStallionFoaled1810CountryUnited Kingdom of Great Britain and IrelandColourBlackBreederCharles BunburyOwner1) Charles Bunbury 2) Richard Wilson 3) John TheobaldTrainerCrouchRecord8: 7‚Äď0‚Äď1Major winsEpsom Derby (1813) 2,000 Guineas Stakes (1813) Smolensko (1810 ‚Äď 10 January 1829) was a Thoroughbred racehorse that won the 1813 Epsom Derby and 2,000 Guineas...

–ß–į—Ā—ā–ł–Ĺ–į —Ā–Ķ—Ä—Ė—ó –Ņ—Ä–ĺ–§—Ė–Ľ–ĺ—Ā–ĺ—Ą—Ė—ŹLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, Averroes–ü–Ľ–į—ā–ĺ–Ĺ–ö–į–Ĺ—ā–Ě—Ė—Ü—ą–Ķ–Ď—É–ī–ī–į–ö–ĺ–Ĺ—Ą—É—Ü—Ė–Ļ–ź–≤–Ķ—Ä—Ä–ĺ–Ķ—Ā –§—Ė–Ľ–ĺ—Ā–ĺ—Ą–ł –ē–Ņ—Ė—Ā—ā–Ķ–ľ–ĺ–Ľ–ĺ–≥–ł –ē—Ā—ā–Ķ—ā–ł–ļ–ł –ē—ā–ł–ļ–ł –õ–ĺ–≥—Ė–ļ–ł –ú–Ķ—ā–į—Ą—Ė–∑–ł–ļ–ł –°–ĺ—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ-–Ņ–ĺ–Ľ—Ė—ā–ł—á–Ĺ—Ė —Ą—Ė–Ľ–ĺ—Ā–ĺ—Ą–ł –Ę—Ä–į–ī–ł—Ü—Ė—ó –ź–Ĺ–į–Ľ—Ė—ā–ł—á–Ĺ–į –ź—Ä—Ė—Ā—ā–ĺ—ā–Ķ–Ľ—Ė–≤—Ā—Ć–ļ–į –ź—Ą—Ä–ł–ļ–į–Ĺ—Ā—Ć–ļ–į –Ď–Ľ–ł–∑—Ć–ļ–ĺ—Ā—Ö—Ė–ī–Ĺ–į —Ė—Ä–į–Ĺ—Ā—Ć–ļ–į –Ď—É–ī–ī—Ė–ĻÔŅĹ...

ŔÖōĻōĪŔÉō© ōĪō£ō≥ ō≥ō®ōßōĪō∑ŔäŔĄ ō¨ō≤ō° ŔÖŔÜ ōßŔĄō≠ōĪō® ōßŔĄō£ŔáŔĄŔäō© ōßŔĄō•ō≥ō®ōßŔÜŔäō© ōßŔĄō™ōßōĪŔäōģ 29 ō≥ō®ō™ŔÖō®ōĪ 1936 ōßŔĄō®ŔĄōĮ ō•ō≥ō®ōßŔÜŔäōß ōßŔĄŔÖŔąŔāōĻ ōĪō£ō≥ ō≥ō®ōßōĪō∑ŔäŔĄ[1] 36¬į14‚Ä≤47‚Ä≥N 4¬į38‚Ä≤30‚Ä≥W / 36.24638889¬įN 4.64166667¬įW / 36.24638889; -4.64166667 [1] ōßŔĄŔÖō™ō≠ōßōĪō®ŔąŔÜ ōßŔĄō¨ŔÖŔáŔąōĪŔäō© ōßŔĄō•ō≥ō®ōßŔÜŔäō© ō¨ō®Ŕáō© ōßŔĄŔÖō™ŔÖōĪōĮŔäŔÜ ōßŔĄŔāŔąō© 2 ŔÖōĮŔÖōĪō© 1 ō∑ōĪōßōĮ ōęŔāŔäŔĄ1 ō∑ōĪōß...

Prime minister of Grenada (1942‚Äď2012) The Right HonourableGeorge Ignatius BrizanCMG CBE8th Prime Minister of GrenadaIn office1 February 1995 ‚Äď 22 June 1995MonarchElizabeth IIGovernor‑GeneralReginald PalmerPreceded byNicholas BrathwaiteSucceeded byKeith Mitchell Personal detailsBorn(1942-10-31)31 October 1942Windsor Forest, GrenadaDied18 February 2012(2012-02-18) (aged 69)St. George's, GrenadaPolitical partyNational Democratic CongressAlma materUniversity of the West I...

Swedish group ABBA topped the chart with The Winner Takes It All Adult Contemporary is a chart published by Billboard ranking the top-performing songs in the United States in the adult contemporary music (AC) market. In 1981, 20 songs topped the chart, based on playlists submitted by radio stations.[1] In the year's first issue of Billboard the number one position was held by British singer Leo Sayer with More Than I Can Say, which retained the top spot from the last week of 1980. ...

Distraction-reducing helmet The Isolator helmet The Isolator was a helmet created by Hugo Gernsback in 1925 to reduce distractions.[1][2] The Isolator was first introduced in the July 1925 edition of the American Physical Society magazine, with which Gernsback was affiliated.[1][3] The helmet was first created using wood and felt.[4] The mouth of the helmet had a baffle for breathing and had three pieces of glass so that users could see outside.[5&#...

Election 1940 Massachusetts gubernatorial election ← 1938 November 5, 1940 (1940-11-05) 1942 → Nominee Leverett Saltonstall Paul A. Dever Party Republican Democratic Popular vote 999,223 993,635 Percentage 49.74% 49.46% County results Municipality resultsSaltonstall: 40‚Äď50% 50‚Äď60% 60‚Äď70% 70‚Äď80% ...

ŔáōįŔá ōßŔĄŔÖŔāōßŔĄō© Ŕäō™ŔäŔÖō© ō•ōį ō™ōĶŔĄ ō•ŔĄŔäŔáōß ŔÖŔāōßŔĄōßō™ ō£ōģōĪŔČ ŔāŔĄŔäŔĄō© ō¨ōĮŔčōß. ŔĀō∂ŔĄŔčōßōĆ ō≥ōßōĻōĮ ō®ō•ō∂ōßŔĀō© ŔąōĶŔĄō© ō•ŔĄŔäŔáōß ŔĀŔä ŔÖŔāōßŔĄōßō™ ŔÖō™ōĻŔĄŔāō© ō®Ŕáōß. (ŔÖōßōĪō≥ 2019) ō£ŔĄŔäōģōßŔÜōĮōĪŔą ŔĀŔäŔĄŔäō®Ŕä ō®ōßŔąŔĄōß ŔÖōĻŔĄŔąŔÖōßō™ ōīōģōĶŔäō© ōßŔĄŔÖŔäŔĄōßōĮ ō≥ŔÜō© 1937 ŔÉŔąōĪōßō≥ōßŔą ō™ōßōĪŔäōģ ōßŔĄŔąŔĀōßō© 13 ō£ōļō≥ō∑ō≥ 2018 (80–81 ō≥ŔÜō©) ŔÖŔąōßō∑ŔÜō© ŔÖŔÖŔĄŔÉō© ŔáŔąŔĄŔÜōĮōß ōßŔĄō≠Ŕäōßō© ōßŔĄōĻŔÖŔĄŔäō© ōßŔĄŔÖŔáŔÜō© ō≥Ŕäōßō≥Ŕä...

Argentine national news agency TélamTelenoticiosa AmericanaTélam headquarters in Buenos AiresNews agency overviewFormedApril 14, 1945DissolvedJuly 2024; 11 days ago (July 2024)[1]JurisdictionArgentinaHeadquartersBuenos AiresEmployees750 [2]Parent News agencySecretary of Media and Public CommunicationWebsitetelam.com.ar Télam (an acronym for Telenoticiosa Americana)[3] was an Argentine government-ran national news agency founded in 1945 by then Secretary...
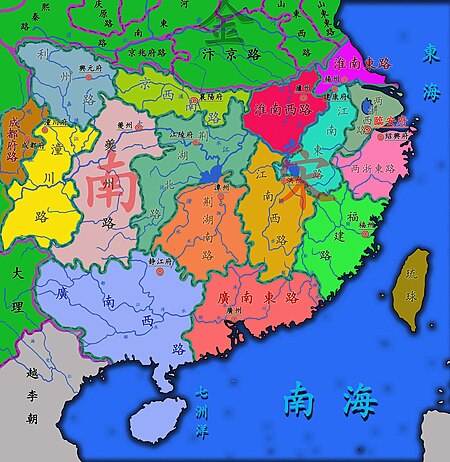
ÁúČŚ∑ěԾƚł≠ŚõĹŚćóŚĆóśúĚśó∂ŤģĺÁĹģÁöĄŚ∑ě„Äā Ť•Ņť≠ŹŚļüŚłĚšļĆŚĻīÔľą553ŚĻīԾȌĻ≥ŤúÄԾƜ¨°ŚĻīśĒĻťĚíŚ∑ěšłļÁúČŚ∑ěԾƜ≤ĽśČÄŚú®ťÄöšĻČŚéŅÔľąŚĆóŚĎ®śĒĻŚģČšĻźŚéŅԾƌźéśĒĻťĹźťÄöŚéŅԾƝö茟ćŚĻŅťÄöŚéŅԾƌ§ćŚźćťÄöšĻČŚéŅԾƌģčśĒĻÁúČŚĪĪŚéŅ„ÄāšĽäŚõõŚ∑ĚÁúĀÁúČŚĪĪŚłāԾȄÄāťöčśúĚŚ§ßšłöŚąĚŚĻīŚļü„ÄāŚĒźśúĚś≠¶Śĺ∑šļĆŚĻīÔľą619ŚĻīԾȌ§ćÁĹģ„ÄāšłčŤĺĖťÄöšĻČŚéŅ„ÄĀťöÜŚĪĪŚéŅÔľąŚÖąŚ§©ŚÖÉŚĻīśĒĻšłļŚĹ≠ŚĪĪŚéŅԾȄÄĀťĚíÁ•ěŚéŅ„ÄĀšłĻś£ĪŚéŅ„ÄĀśī™ťõÖŚéŅ„ÄĀŚćóŚģČŚéŅÔľąšĽäŚõõŚ∑ĚÁúĀŚ§ĻśĪüŚéŅśú®ŚüéťēáԾƜ≠¶Śĺ∑šļĒŚĻīÁúĀԾȄÄāŚ§©ŚģĚ„ÄĀšĻĺŚÖÉśó∂ÔŅĹ...

List of administrative divisions in France Politics of French Polynesia President of France Emmanuel Macron High Commissioner of the Republic √Čric Spitz President of French Polynesia Moetai Brotherson Council of Ministers Assembly of French Polynesia President: Antony G√©ros Political parties Elections Parliamentary: 2013, 2018, 2023 Referendums: 1940, 1958 Administrative divisions Other countries vte In French Polynesia, there are two levels of administrative divisions: five administrative ...

Arbre g√©n√©alogique de la dynastie Keita. Fond√©e par Soundiata Keita en 1235, qui fut le premier Mansa, ou Empereur, cette dynastie a marqu√© l'histoire avec des figures embl√©matiques comme Mansa Moussa qui monta sur le tr√īne en 1312 et pr√©sida √† l'apog√©e de l'Empire du Mali. Cependant, apr√®s des si√®cles de grandeur, la dynastie a vu son dernier souverain r√©gnant, Mahmud IV, r√©gner jusqu'en 1610. Son r√®gne fut marqu√© par la chute de l'Empire, entra√ģn√©e par la d√©faite de la bat...

De Atik Mustafa Pasha moskee, voorheen de Kerk van de heilige Petrus, in Istanboel 1059 Eeuwen: 10e eeuw ¬∑ 11e eeuw ¬∑ 12e eeuw Decennia: 1040-1049 ¬∑ 1050-1059 ¬∑ 1060-1069 Jaren: << ¬∑ < ¬∑ 1058 ¬∑ 1059 ¬∑ 1060 ¬∑ > ¬∑ >> Jaartelling in verschillende culturen Ab urbe condita: 1812 MDCCCXII Armeense jaartelling: 507 ‚Äď 508‘Ļ’é ’á‘∑ ‚Äď ’á‘ł Chinese jaartelling: 3755 ‚Äď 375...
