K理論
|
Read other articles:

Wu JiaduoOutfitting the Olympic team of Germany 2012Personal informationJulukanDuduKebangsaan Tiongkok / JermanTempat tinggalDüsseldorf, JermanLahir19 September 1977 (umur 46)[1]Linhai, Zhejiang, TiongkokGaya bermainTangan kanan, shakehand gripPeringkat tertinggi11 (Juli – Agustus 2010)[2]KlubFSV KroppachTinggi165 m (541 ft 4 in)Berat54 kg (119 pon; 8,5 st) Wu Jiaduo (Hanzi sederhana: 吴佳多; Hanzi tradisional: 吳佳...
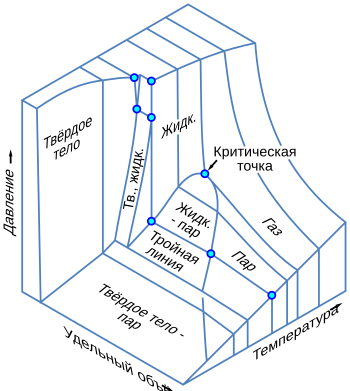
–¢–∏–ø–∏—á–Ω—ã–µ –≤–∏–¥—ã —Ñ–∞–∑–æ–≤—ã—Ö –¥–∏–∞–≥—Ä–∞–º–º. –ó–µ–ª—ë–Ω—ã–π –ø—É–Ω–∫—Ç–∏—Ä –ø–æ–∫–∞–∑—ã–≤–∞–µ—Ç –∞–Ω–æ–º–∞–ª—å–Ω–æ–µ –ø–æ–≤–µ–¥–µ–Ω–∏–µ –≤–æ–¥—ã –¢—Ä—ë—Ö–º–µ—Ä–Ω–∞—è —Ñ–∞–∑–æ–≤–∞—è –¥–∏–∞–≥—Ä–∞–º–º–∞ –§–∞–∑–æ–≤–∞—è –¥–∏–∞–≥—Ä–∞–º–º–∞ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω–æ–π —Å–µ—Ä—ã. Sp ‚Äî —Ä–æ–º–±–∏—á–µ—Å–∫–∞—è —Å–µ—Ä–∞; S–º ‚Äî –º–æ–Ω–æ–∫–ª–∏–Ω–Ω–∞—è —Å–µ—Ä–∞; S–∂ ‚Äî –∂–∏–¥–∫–∞—è —Å–µ—Ä–∞; S–ø ‚Äî –ø–∞—Ä—ã —Å–µ—Ä—ã –Ý ‚Äî –¥–∞–≤–ª–µ–Ω–∏–µ, –¢ ‚Äî —Ç–µ–º–ø–µ—Ä–∞—Ç—ÉÔøΩ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Johnny GormanInformasi pribadiNama lengkap Rory John McCaughan GormanTanggal lahir 26 Oktober 1992 (umur 31)Tempat lahir Sheffield, InggrisTinggi 1,78 m (5 ft 10 in)Posisi bermain Gelandang sayapInformasi klubKlub saat ini BarrowKa...

العلاقات السنغالية المالاوية السنغال مالاوي السنغال مالاوي تعديل مصدري - تعديل العلاقات السنغالية المالاوية هي العلاقات الثنائية التي تجمع بين السنغال ومالاوي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

American photographer and educator Harry Morey CallahanBorn(1912-10-22)October 22, 1912Detroit, MichiganDiedMarch 15, 1999(1999-03-15) (aged 86)Atlanta, GeorgiaNationalityAmericanAwardsEdward MacDowell Medal 1993 National Medal of Arts 1996 Harry Morey Callahan (October 22, 1912 – March 15, 1999) was an American photographer and educator.[1][2] He taught at both the Institute of Design in Chicago and the Rhode Island School of Design. Callahan's first solo exhibition wa...

Argentine footballer and manager (1935–2021) Vicente Cantatore Personal informationFull name Vicente Cantatore SocciDate of birth (1935-10-06)6 October 1935Place of birth Rosario, ArgentinaDate of death 15 January 2021(2021-01-15) (aged 85)Place of death Valladolid, SpainPosition(s) MidfielderYouth career Talleres de BelgranoSenior career*Years Team Apps (Gls)1953 Talleres de Belgrano 1955–1958 San Lorenzo 8 (0)1959 Tigre 4 (0)1960–1963 Rangers 1964–1970 Santiago Wanderers 1971�...

You can help expand this article with text translated from the corresponding article in Turkish. (January 2022) Click [show] for important translation instructions. View a machine-translated version of the Turkish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wiki...
Cet article est une √©bauche concernant Francisco de Goya. Vous pouvez partager vos connaissances en l‚Äôam√©liorant (comment ?) selon les recommandations des projets correspondants. Le Sacrifice √Ý PanEl Sacrificio a PanArtiste Francisco de GoyaDate 1771Type RomantismeTechnique Huile sur toileDimensions (H √ó L) 33 √ó 24 cmPropri√©taire Jos√© GudiolLocalisation Collection priv√©e Jos√© Gudiol, Barcelone (Espagne)Protection Class√© BIC (1991)modifier - modif...

L'√âglise constitutionnelle √©tait l'√âglise institu√©e et organis√©e par la Constitution civile du clerg√© (1790) et constitu√©e d'√©v√™ques, de pr√™tres, de diacres et de clercs ayant pr√™t√© le serment exig√©. Cette √âglise constitutionnelle est d√©clar√©e schismatique par le pape Pie VI. Les membres du clerg√© ayant pr√™t√© serment (√Ý la Constitution civile du clerg√©) √©taient appel√©s ¬´ jureurs ¬ª ou ¬´ asserment√©s ¬ª, par opposition aux ¬´ inserment√©s ...

The White Angel fresco from Mileševa Monastery (1235) Serbian Orthodox Monastery of Dečani, built in the 14th century, UNESCO World Heritage Site Serbian art refers to the visual arts of the Serbs and their nation-state Serbia. The medieval heritage includes Byzantine art, preserved in architecture, frescos and icons of the many Serbian Orthodox monasteries. In the early modern period, Serbian visual arts began to be influenced by Western art, culminating in the Habsburg monarchy in the lat...

Konvensi mengenai Kerja Paksa atau dalam Bahasa Inggris disebut sebagai Forced Labor Convention, 1930 (No.29) merupakan instrumen internasional pertama yang dikeluarkan oleh organisasi perburuhan dunia atau International Labor Organization (ILO) yang secara khusus membahas mengenai Kerja Paksa atau Wajib Kerja. Konvensi ini disahkan atau diadopsi pada 28 Juni 1930 di Jenewa, Swiss dan mulai berlaku pada 1 Mei 1932.[1] Terdapat dua konvensi yang dikeluarkan oleh ILO terkait dengan kerj...

–í —Å—Ç–∞—Ç—å–µ –µ—Å—Ç—å —Å–ø–∏—Å–æ–∫ –∏—Å—Ç–æ—á–Ω–∏–∫–æ–≤, –Ω–æ –Ω–µ —Ö–≤–∞—Ç–∞–µ—Ç —Å–Ω–æ—Å–æ–∫. –ë–µ–∑ —Å–Ω–æ—Å–æ–∫ —Å–ª–æ–∂–Ω–æ –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å, –∏–∑ –∫–∞–∫–æ–≥–æ –∏—Å—Ç–æ—á–Ω–∏–∫–∞ –≤–∑—è—Ç–æ –∫–∞–∂–¥–æ–µ –æ—Ç–¥–µ–ª—å–Ω–æ–µ —É—Ç–≤–µ—Ä–∂–¥–µ–Ω–∏–µ. –í—ã –º–æ–∂–µ—Ç–µ —É–ª—É—á—à–∏—Ç—å —Å—Ç–∞—Ç—å—é, –ø—Ä–æ—Å—Ç–∞–≤–∏–≤ —Å–Ω–æ—Å–∫–∏ –Ω–∞ –∏—Å—Ç–æ—á–Ω–∏–∫–∏, –ø–æ–¥—Ç–≤–µ—Ä–∂–¥–∞—é—â–∏–µ –∏–Ω—Ñ–æ—Ä–º–∞—Ü–∏—é. –°–≤–µ–¥–µ–Ω–∏—è –±–µ–∑ —Å–Ω–æ—Å–æ–∫ –º–æ–≥—É—Ç –±—ã—Ç—å —É–¥–∞–ª–µ–Ω—ã. (24 –∏—éÔøΩ...

Owen WilsonWilson tahun 2011LahirOwen Cunningham Wilson[1]18 November 1968 (umur 55)[2]Dallas, Texas, Amerika SerikatAlmamaterUniversitas Texas di AustinPekerjaanAktorproduserpenulis skenarioTahun aktif1994–sekarangAnak3KerabatLuke Wilson (adik kandung) Owen Cunningham Wilson (lahir 18 November 1968)[3] adalah seorang aktor asal Amerika Serikat. Dia memiliki hubungan panjang perfilman dengan pembuat film Wes Anderson, di mana mereka bekerja sama dalam penu...

••ÊûóÂåπÂÖãËøêÂ䮉ºöÂç¢Êó∫Ëæ扪£Ë°®ÂúòÂç¢Êó∫ËææÂõΩÊóóIOCÁ∑®Á¢ºRWANOCÁõßÂÆâÈÅîÂúãÂÆ∂•ßÊûóÂåπÂÖãÂèäÈ´îËÇ≤ÂßîÂì°ÊúÉÁ∂≤Á´ôolympicrwanda.orgÔºàËã±ÊñáÔºâÂéܱ䕕ÊûóÂåπÂÖãËøêÂ䮉ºöÂèÇ˵õËÆ∞ÂΩïÔºàÊĪÁªìÔºâ§èÂ≠£Â••ÊûóÂåπÂÖãËøêÂ䮉ºö19841988199219962000200420082012201620202024 Âç¢Êó∫ËææËá™1984Âπ¥ÊØèÂπ¥Â§èÂ≠£Â•ßÊûóÂåπÂÖãÈÅãÂãïÊúÉÁöÜÊúâÊ¥æÂì°ÂèÉËàáÔºåÊà™Ëá≥ÁõÆÂâçÁÇ∫Ê≠¢Ë©≤ÂúãÂ∞öÊú™ÂèÉÂäÝÈÅéÂܨÂ≠£Â•ßÊûóÂåπÂÖãÈÅãÂãïÊúÉ„ÄÇ Ë©≤ÂúãËøщªäÂ∞öÊú™Ë¥èÂæ󉪪‰Ωï‰∏ÄÈù¢Â•ßÈÅãÊúÉÁçéÁâåÔºå‰ΩÜÁî∞ÂæëÈÅ∏ÊâãJean de Dieu ...

Scottish singer and songwriter (born 1987) Emeli SandéMBESandé in 2014Background informationBirth nameAdele Emily SandéBorn (1987-03-10) 10 March 1987 (age 37)[1]Sunderland, Tyne and Wear, EnglandOriginAberdeen, ScotlandOccupation(s) Singer songwriter Years active2008–presentSpouse(s) Adam Gouraguine (m. 2012; div. 2014)Websiteemelisande.comMusical careerGenres R&B soul gospel Instrument(s) Vocals piano Labels Virgin Vi...

Species of New World monkey Yellow-tailed woolly monkey[1] Conservation status Critically Endangered (IUCN 3.1)[2] CITES Appendix I (CITES)[3] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Atelidae Genus: Lagothrix Species: L. flavicauda Binomial name Lagothrix flavicauda(Humboldt, 1812) Synonyms Oreonax flavicauda Thomas, 1927 Lagothrix...

Stone construction, typically found on St. Kilda, Scotland A cleit on St Kilda (overlooking Village Bay) A cleit at the Cleitein McPhaidein, Boreray A cleit is a stone storage hut or bothy, uniquely found on the isles and stacs of St Kilda; whilst many are still to be found, they are slowly falling into disrepair.[1] There are known to be 1,260 cleitean on Hirta and a further 170 on the other St Kilda-group islands.[2][1] The outlying island of Boreray has the Cleitean...

Italian Renaissance architect (1377–1446) Brunelleschi redirects here. For other uses, see Brunelleschi (disambiguation). Filippo BrunelleschiAnonymous portrait from the 2nd half of the 15th century (Louvre, Paris)BornFilippo di ser Brunellesco di Lippo Lapi[1]1377Florence, Republic of FlorenceDied15 April 1446(1446-04-15) (aged 68–69)Florence, Republic of FlorenceKnown forArchitecture, sculpture, mechanical engineeringNotable workDome of Santa Maria del FioreMovementEar...
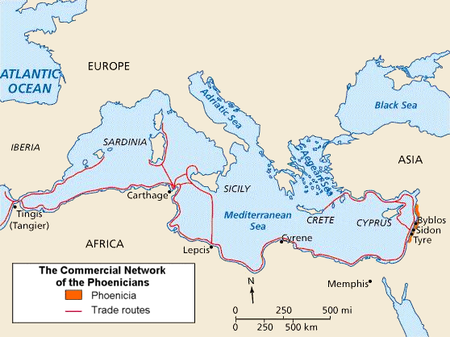
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Carthaginian Iberia – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this message) Place in CarthaginianIberiaIberian Lady of Elche, 4th century BC, maybe influenced by CarthaginianMap of the western Mediterranean and Ca...

У этого термина существуют и другие значения, см. Дике (значения). Дикедр.-греч. Δίκη Дике Сфера влияния правосудие[вд][1] Пол женский[1] Отец Зевс[2][1] или Nomos[вд] Мать Фемида[2][1] или Eusebia[вд] Братья и сёстры Эвномия[1] и Эйрена[1] В иных к�...





