1-形式
|
Read other articles:

Christian Ramos Christian Ramos Rusia 2018Informasi pribadiNama lengkap Christian RamosTanggal lahir 4 November 1988 (umur 35)Tempat lahir Lima, PeruTinggi 182 cm (6 ft 0 in)Posisi bermain BekInformasi klubKlub saat ini VeracruzNomor 2Karier senior*Tahun Tim Tampil (Gol)2018 – Veracruz 8 (0)Tim nasional2009 – Peru 69 (3) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Christian Ramos (lahir 4 November 1988) adalah seorang pemain sepak bola berkew...

Dorce Sok AkrabSutradaraYazman YazidProduserRaam PunjabiDitulis olehDeddy ArmandPemeranDorce GamalamaKadirEko DJDoyokNurul ArifinJohny KaneHIM DamsyikSukarsihPak TileAcha HasanuddinDoddy SukmaRuslan EffendyWaylan GerungIta Puspita SariErna KurniawatiPenata musikBuche ChekingSinematograferSubakti ISPenyuntingBenny MSDistributorParkit FilmTanggal rilis1989Durasi84 menitNegaraIndonesia Dorce Sok Akrab adalah sebuah film Indonesia dirilis tahun 1989 yang disutradarai oleh Yazman Yazid serta...

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Lingka...

مهدي أخوان ثالث معلومات شخصية الميلاد 1347 هـمشهد الوفاة 1411 هـطهران مكان الدفن مشهد مواطنة قصر بهلوي (1929–1979) إيران (1979–1990) الحياة العملية الاسم الأدبي م. اميد المهنة شاعر اللغات الفارسية بوابة الأدب تعديل مصدري - تعديل مهدي أخوان ثالث ( 1347 - 1411 هـ / 1929 - 1990 م ) هو شا�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. SDN Kramat Jati 09Sekolah Dasar Negeri Kramat Jati 09InformasiJenisNegeriNomor Pokok Sekolah Nasional20108791Jumlah siswa173 2010StatusAktifAlamatLokasiKramat Jati, Jakarta Timur, DKI Jakarta, IndonesiaSitus webLaman di Kementerian Pendidika...

ميّز عن معركة سيف القدس. لمعانٍ أخرى، طالع الحرب على غزة. الاشتباكات الإسرائيلية الفلسطينية 2021 جزء من القضية الفلسطينية لافتة كتب عليها أنقذوا حي الشيخ جراح على أحد أسوار حي الشيخ جراح في مدينة القدس في 9 مايو 2021 التاريخ 6 مايو 2021 - 21 مايو 2021 المكان إسرائيل�...
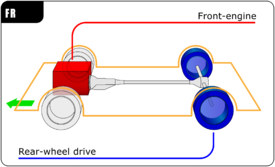
Layout of a motorised vehicle The powertrain layout of a motorised vehicle such as a car is often defined by the location of the engine or motors and the drive wheels. Layouts can roughly be divided into three categories: front-wheel drive (FWD), rear-wheel drive (RWD) and four-wheel drive (4WD). Many different combinations of engine location and driven wheels are found in practice, and the location of each is dependent on the application for which the vehicle will be used. Front-wheel-drive ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的...

Indigenous people living in areas of Venezuela, Brazil, and Guyana For the language, see Pemon language. PemonPemon boy, VenezuelaTotal populationc. 31,440Regions with significant populations Venezuela30,148 (2011)[1] Brazil792 (2014)[2] Guyanac. 500[3]LanguagesPemon, SpanishReligiontraditional tribal religion, Roman Catholicism[4] The Pemon or Pemón (Pemong) are indigenous people living in areas of Venezuela, Brazil, and Guyana.[5] The ...

Opera by César Cui Composer César Cui 19th-century postcard of Mount Elbrus in the Caucasus Mountains Prisoner of the Caucasus (Кавказский пленник in Cyrillic, Kavkazskij plennik in transliteration) is an opera in three acts, composed by César Cui. The libretto is credited to Viktor Krylov, and is based on Alexander Pushkin's 1822 poem The Prisoner of the Caucasus. The English title has been rendered also as Prisoner in the Caucasus and The Captive in the Caucasus. The ope...

Starčevo cultureHorizonFirst Temperate Neolithic, Old EuropePeriodNeolithic EuropeDatescirca 6,200 B.C.E. — circa 4,500 B.C.E.Type siteStarčevo sitePreceded byIron Gates culture, Lepenski Vir culture, Sesklo culture, Neolithic GreeceFollowed byKaranovo culture, Vinča culture, Tisza culture, Hamangia culture, Gumelnița culture, Kakanj culture, Sopot culture, Linear Pottery culture See also: Old Europe (archaeology) and Danube civilization The Starčevo culture is an archaeological cultur...

Districts of Tajikistan Districts of Tajikistan, situation before 2017 Politics of Tajikistan CIS Member State Constitution Human rights Government President (list) Emomali Rahmon Prime Minister Kokhir Rasulzoda Cabinet Legislature Supreme Assembly National Assembly Assembly of Representatives Elections Recent elections Presidential: 20132020 Parliamentary: 20152020 Political parties Administrative divisions Regions Districts Jamoats Foreign relations Ministry of Foreign Affairs Minister: Sir...

Anhe Ghore Da DaanSutradaraGurvinder SinghProduserPerusahaan Pengembangan Film Nasional IndiaDitulis olehGurdial SinghGurvinder SinghPenata musikCatherine LambSinematograferSatya Rai NagpaulPenyuntingUjjwal ChandraTanggal rilis 11 Oktober 2011 (2011-10-11) (Festival Film Internasional Pusan) NegaraIndiaBahasaPunjabi Anhe Ghore Da Daan (bahasa Punjabi: ਅੰਨ੍ਹੇ ਘੋੜੇ ਦਾ ਦਾਨ|bahasa Inggris: Alms for a Blind Horse) adalah sebuah film berbahasa Pu...

В Википедии есть статьи о других людях с такой фамилией, см. Сапиев. Серик Сапиев Общая информация Полное имя Серик Жумангалиевич Сапиев Гражданство Казахстан Дата рождения 16 ноября 1983(1983-11-16) (40 лет) Место рождения Абай, Карагандинская область, Казахская ССР, СССР Весо�...

Open standard for office applications Uniform Office FormatFilename extension .uof, .uot, .uos, .uopInitial releaseApril 30, 2007; 17 years ago (2007-04-30)Latest release2.02011; 13 years ago (2011) Type of formatDocument file formatExtended fromXML, SVGStandardGB/T20916-2007Open format?Yes Uniform Office Format (UOF; Chinese 标文通, literally standard text general[1]), sometimes known as Unified Office Format, is an open standard for office...

American moral philosopher (1908–1994) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2020) (Learn how and when to remove this message) William FrankenaWilliam Frankena in 1949Born(1908-06-21)June 21, 1908Manhattan, Montana, U.S.DiedOctober 22, 1994(1994-10-22) (aged 86)Ann Arbor, Michigan, U.S.Alma materCalvin CollegeUniversity of MichiganH...

تيموثي غايتنر وزير الخزانة الأمريكي في المنصب26 يناير 2009 – 25 يناير 2013 الرئيس باراك أوباما هنري بولسون جاكوب ليو معلومات شخصية الميلاد 18 أغسطس 1961 (العمر 63 سنة)بروكلين مواطنة الولايات المتحدة عضو في مجموعة الثلاثين[1] عدد الأولاد 2 الحياة العملية المدرسة...
Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Junho de 2022) SÉCULOS: Século XIII — Século XIV — Século XV DÉCADAS: 1280 • 1290 • 1300 • 1310 • 1320 • 1330 • 1340 • 1350 • 1360 • 1370 • 1380 ANOS: 1334 • 1335 • 1336 • 1337 • 1338 • 1339 • 1340 • 13...

American college basketball season 2021–22 Troy Trojans men's basketballParadise Classic championCBI, First RoundConferenceSun Belt ConferenceRecord20–12 (10–6 Sun Belt)Head coachScott Cross (3rd season)Assistant coaches Kenneth Mangrum Byron Jones Mike Worley Home arenaTrojan Arena (Capacity 6,000)Seasons← 2020–212022–23 → 2021–22 Sun Belt Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT Texas ...




![{\displaystyle \operatorname {mean} (v)=[1/n,1/n,\dots ,1/n]\cdot v.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d73c1b9f5555aa81a77de1dbdfa507db285c5566)






