農心辛ラーメン杯世界囲碁最強戦
|
Read other articles:

Questa voce o sezione sull'argomento Islanda non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Coordinate: 65°30′N 24°30′W / 65.5°N 24.5°W65.5; -24.5 La posizione di Látrabjarg a Vestfirðir. L'estremita occidentale della penisola, con il faro Látrabjarg è l'estremità più occidentale dell'isola dell'Islanda ed è anche il punto...

Ini adalah nama Batak Angkola, marganya adalah Siregar. Zivanna Letisha SiregarZivanna di Qur'an Indonesia ProjectLahirZivanna Letisha Siregar16 Februari 1989 (umur 35)Jakarta, IndonesiaNama lainZivanna LetishaZiziPekerjaanModel, Ratu kecantikan, Penulis, Filantropis, PresenterTahun aktif2008 - sekarangTinggi178 cm (5 ft 10 in)Suami/istriHaries Argareza Harahap (m. 2016)Anak3 Zivanna Letisha SiregarPemenang kontes kecantikan...

Peter Lamborn WilsonLahir1945 (1945)Meninggal22 Mei 2022(2022-05-22) (umur 76–77)EraFilsafat abad ke-20KawasanFilsafat BaratAliranPasca-anarkisme, anarkisme individualis[1]Minat utamaPenolakan kerja, masyarakat pasca-industri, mistisisme, utopianisme, pederastiGagasan pentingZona otonom sementara Dipengaruhi Charles Fourier, Robert Anton Wilson, Timothy Leary Memengaruhi Michael Muhammad Knight Salinan Pirate Utopias yang ditandatangani Wilson Peter Lamborn Wils...

Not to be confused with 3-Methoxymorphinan. Morphinan Names IUPAC name Morphinan[1] Systematic IUPAC name (4aR,10R,10aR)-1,3,4,9,10,10a-Hexahydro-2H-10,4a-(azanoethano)phenanthrene Identifiers CAS Number 468-10-0 Y 3D model (JSmol) Interactive image Beilstein Reference 1375527 ChEBI CHEBI:35649 N ChemSpider 5256833 Y PubChem CID 11947744 UNII O97T9O1050 Y CompTox Dashboard (EPA) DTXSID00425890 InChI InChI=1S/C16H21N/c1-2-6-13-12(5-1)11-15-14-7-3-4-8-16(13,14)9-10-1...

Area of the East End of London, England Human settlement in EnglandBlackwallVirginia Quay, the line that runs down the centre of the avenue marking the prime meridianBlackwallShow map of London Borough of Tower HamletsBlackwallLocation within Greater LondonShow map of Greater LondonPopulation19,461 (2011 Census. Blackwall and Cubitt Town Ward)[1]OS grid referenceTQ385805London boroughTower HamletsCeremonial countyGreater LondonRegionLondonCountryEnglandSoverei...

Indian Carnatic music singing duo Bombay SistersBackground informationBorn C. Saroja (1936-12-07) 7 December 1936 (age 87) Trichur, Kerala C. Lalitha (1938-08-26)26 August 1938 Trichur Kerala, Died C. Lalitha 31 January 2023(2023-01-31) (aged 84) Chennai, India GenresCarnatic musicEducationS.I.E.S MatungaAlma materDelhi UniversityAwardsPadma Shri (2020) Musical artist The Bombay Sisters, C. Saroja (born 7 December 1936) and C. Lalitha (26 August 1938 – 31 January 2023), were ...

Indonesian actor (1924–1992) A. Hamid AriefA. Hamid Arief, c. 1960BornAbdul Hamid Arief(1924-11-25)25 November 1924Batavia, Dutch East IndiesDied20 December 1992(1992-12-20) (aged 68)Jakarta, IndonesiaNationalityIndonesianOccupationActor Abdul Hamid Arief (25 November 1924 – 20 December 1992) was an Indonesian actor who appeared in more than 120 films. Born in Batavia, Dutch East Indies, he started his acting career in theatre before migrating to film with 1948's Anggrek Bu...

1965 film by Sidney Hayers Three Hats for LisaUK poster by Tom ChantrellDirected bySidney HayersWritten byDavid D. OsbornScreenplay byLeslie BricusseTalbot RothwellProduced byJack HanburyStarringJoe BrownSophie HardySid JamesUna StubbsDave NelsonCinematographyAlan HumeEdited byTristam ConesMusic byLeslie Bricusse (songs)Eric RogersProductioncompanySeven Hills ProductionsDistributed byAnglo-Amalgamated Film Distributors (UK)Release date May 30, 1965 (1965-05-30) Running time99 m...

Disambiguazione – Se stai cercando l'omonimo film, vedi Il corvo - Preghiera maledetta. Disambiguazione – Se stai cercando l'album omonimo, vedi The Cult (album). Questa voce o sezione sull'argomento gruppi musicali britannici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. The CultThe Cult live nel 2...

Seri Dragon BallGambar sampul Kemelut Dragon Ball.MangaAlbum nomor2EpisodeDragon Ball SagaDidahului olehGoku dan Kawan-KawannyaDiikuti denganTenkaichi Budokai DimulaiDiterbitkan di Jepang1984Diterbitkan di Indonesia1992 Kemelut Dragon Ball adalah jilid ke-2 manga Dragon Ball. Pada jilid ini mengisahkan petualangan Goku bersama kawan-kawannya yang baru. Goku untuk pertama kalinya berjumpa dengan Chi-Chi dan ayahnya. lbsSeri Dragon BallDiterbitkan oleh Elex Media KomputindoGoku dan Kawan-Kawann...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Voce principale: Eccellenza 2018-2019. Eccellenza Campania 2018-2019 Competizione Eccellenza Campania Sport Calcio Edizione 28ª Organizzatore F.I.G.C. - L.N.D.Comitato Regionale Campania Date dal 1º settembre 2018al 7 aprile 2019 Paese organizz. Italia Luogo Campania Partecipanti 32 Formula 2 gironi all'italiana, play-off e play-out Risultati Vincitore Giugliano San Tommaso Promozioni Giugliano San Tommaso Retrocessioni Faiano Barano Calcio Virtus Ottaviano Aversa Norma...

关于与「王芳 (政治人物)」標題相近或相同的条目页,請見「王芳」。 王芳本名王春芳出生(1920-09-30)1920年9月30日山东新泰逝世2009年11月4日(2009歲—11—04)(89歲)浙江杭州国籍 中華民國(1920-1949) 中华人民共和国(1949-2009)民族汉族政党 中国共产党 王芳(1920年9月30日—2009年11月4日),原名王春芳,山东新泰人。1937年10月参加革命,1938年4月加入中�...
هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (أبريل 2020) 2020 coronavirus pandemic in the Republic of Artsakh Number of confirmed cases by province (as of 8 April): Confirmed 1–9 �...

British technology journalist (1947–2020) Jack SchofieldSchofield in 2009Born(1947-10-30)30 October 1947Died31 March 2020(2020-03-31) (aged 72)OccupationJournalist Schofield's voice recorded in November 2012 Jack Schofield (30 October 1947 – 31 March 2020)[1] was a British technology journalist. He wrote the Ask Jack column for The Guardian[2] and preceding that covered technology for the newspaper from 1983 to 2010. He edited photography and computing periodicals and...

Tibetan kingdom from 1642-1717 Khoshut Khanateᠬᠣᠱᠤᠳ ᠤᠯᠤᠰ和碩特汗國1642–1717Location of the Khoshut Khanate among Mongol tribesStatusNomadic empireReligion Tibetan BuddhismGovernmentMonarchyHistory • Established 1642• Disestablished 1717 Preceded by Succeeded by Tsangpa Dzungar Khanate Today part ofChina The Khoshut Khanate was a Mongol Oirat khanate based in the Tibetan Plateau from 1642 to 1717. Based in modern Qinghai, it was founded by Güshi Kha...
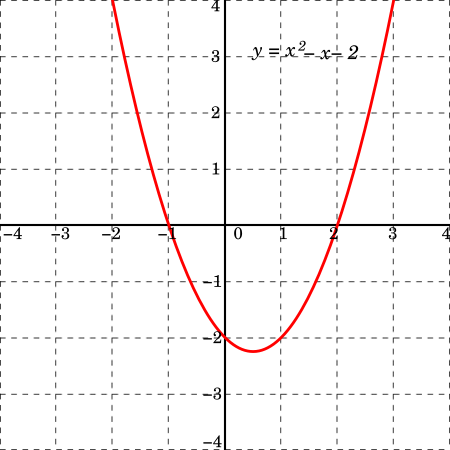
For dependent and independent random variables, see Independence (probability theory). Concept in mathematical modeling, statistical modeling and experimental sciences A variable is considered dependent if it depends on an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable ...

Founder of Glendale, Arizona (1839–1923) For other people named William Murphy, see William Murphy (disambiguation). William John MurphyWilliam John Murphy, c. 1905Born(1839-08-23)August 23, 1839New Hartford, New YorkDiedApril 17, 1923(1923-04-17) (aged 83)Phoenix, ArizonaOccupation(s)Businessman, contractor and land developer William John Murphy (August 23, 1839 – April 17, 1923) was an American businessman, contractor, land developer and founder of the Arizona Improvement Company. ...

Portuguese footballer (born 1997) In this Portuguese name, the first or maternal family name is Reis and the second or paternal family name is Ferreira. Ferro Ferro with Valencia in 2021Personal informationFull name Francisco Reis FerreiraDate of birth (1997-03-26) 26 March 1997 (age 27)Place of birth Oliveira de Azeméis, PortugalHeight 1.91 m (6 ft 3 in)Position(s) Centre backTeam informationCurrent team Hajduk SplitNumber 97Youth career2005–2008 Oliveirense2008–...

Loss of biological wealth of a forest Degraded forest in Lahnberge, Germany: the soil is being washed out due to lack of vegetal cover, some trees are losing ground and they appear to be sick (photo by Andreas Trepte). Forest degradation is a process in which the biological wealth of a forest area is permanently diminished by some factor or by a combination of factors. This does not involve a reduction of the forest area, but rather a quality decrease in its condition. The forest is still the...