ハール測度
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Josias Cornelis Rappard – berita · surat kabar · buku · cendekiawan · JSTOR Rampokan macan, sebuah pertunjukan di Jawa pada masa lampau, di mana seekor harimau Jawa (Panthera tigris sondaica) dikurung da...

Bursa Saham New York simbol dari pasar bebas, tempat dimana para pelaku pasar memperdagangkan saham. Pasar bebas (bahasa Inggris: free market) adalah kondisi pasar ideal, di mana seluruh kegiatan perekonomian sepenuhnya berada pada dinamika permintaan dan penawaran pasar yang akan mempengaruhi keputusan ekonomi dan pergerakan setiap individu yang berhubungan dengan uang, barang, dan jasa secara sukarela. Pasar bebas diadvokasikan oleh pengusul ekonomi liberalisme. Dalam sistem yang murni (lai...

For other places with the same name, see Fort Washington. Census-designated place in MarylandFort Washington, MarylandCensus-designated placeFort Washington Park's main gate in October 2004Location of Fort Washington in MarylandCoordinates: 38°44′37″N 77°0′37″W / 38.74361°N 77.01028°W / 38.74361; -77.01028Country United StatesState MarylandCounty Prince George'sArea[1] • Total16.57 sq mi (42.92 km2) • ...

Tentara Panzer ke-22. Panzerarmeecode: de is deprecated InsigniaAktif5 Juni 1940 – 8 Mei 1945Negara Nazi GermanyCabangTentara WehrmachtTipe unitPanzerPeranPeperangan lapis bajaJumlah personelAngkatan BersenjataPertempuranPerang Dunia II Front Timur TokohTokoh berjasaHeinz Guderian Tentara Panzer ke-2 (Jerman: 2. Panzerarmeecode: de is deprecated ) adalah formasi kendaraan lapis baja Jerman Nazi selama Perang Dunia II yang dibentuk dari Grup Panzer ke-2 pada tanggal 5 Oktober 1941. Grup...

Paraguayan tennis player This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) Ramón DelgadoCountry (sports) ParaguayResidence...

Village in FloridaPalmetto Bay, FloridaVillageVillage of Palmetto Bay FlagSealNickname: Village of ParksLocation in Miami-Dade and the state of Florida.U.S. Census Bureau map showing village boundariesCoordinates: 25°37′37.87″N 80°19′14.53″W / 25.6271861°N 80.3207028°W / 25.6271861; -80.3207028Country United States of AmericaState FloridaCounty Miami-DadeIncorporatedSeptember 10, 2002Government • TypeMayor-Council • M...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Disambiguazione – Se stai cercando la società della città di Várzea Grande, vedi Operário Futebol Clube (Várzea Grande). OperárioCalcio Galo Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Nero, bianco Simboli Gallo Dati societari Città Campo Grande Nazione Brasile Confederazione CONMEBOL Federazione CBF Campionato Campionato Sul-Mato-Grossense Fondazione 1938 Presidente Estevão Petrallas Allenatore Celso Rodrigues Stadio Morenão(29 680 posti) Palmarès ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...
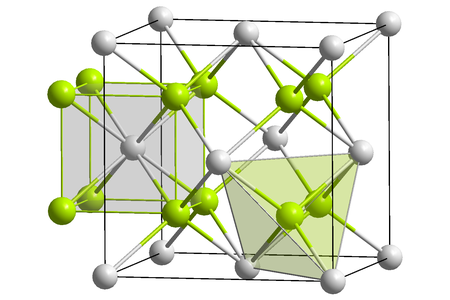
Praseodymium dioxide Names IUPAC name Praseodymium(IV) oxide Identifiers CAS Number 12036-05-4 3D model (JSmol) Interactive image ChemSpider 74758 Y ECHA InfoCard 100.031.658 EC Number 234-838-5 PubChem CID 82846 CompTox Dashboard (EPA) DTXSID0065191 InChI InChI=1S/2O.PrKey: BOWRJOSABXTXBI-UHFFFAOYSA-N SMILES O=[Pr]=O Properties Chemical formula PrO2 Molar mass 172.91 Appearance Dark brownish crystal[1] Structure[2] Crystal structure Fluorite stru...
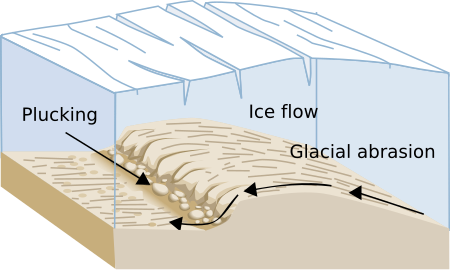
This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2007) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Glacial history of Minnesota – news · ...

Newspaper in Whistler, British Columbia Pique NewsmagazineTypeWeekly newspaperFormatTabloidPublisherSarah StrotherEditorBraden DupuisFoundedNovember 25, 1994Headquarters103-1390 Alpha Lake Road, Whistler, British Columbia, CanadaCirculation16,140 in 2011[1]Websitepiquenewsmagazine.com Pique Newsmagazine is the only newspaper serving the resort community of Whistler, British Columbia. It was founded in 1994 and operated as an independent, locally owned weekly newspaper until July 2013,...

Radio station in Faribault, MinnesotaKBGYSimulcasting KLCI Elk RiverFaribault, MinnesotaFrequency107.5 MHzBrandingBOB Total CountryProgrammingFormatClassic countryAffiliationsCompass Media NetworksWestwood OneOwnershipOwnerDennis and Lucas Carpenter(Carpenter Broadcasting LLC)Sister stationsKLCI, WLKX-FM, WQPMHistoryFirst air date2001Technical informationFacility ID84475ClassC2ERP48,000 wattsHAAT120 meters (390 ft)LinksWebcastListen LiveWebsitemybobcountry.com Logo with former format KBG...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

الجائزة الأدبية هي الجائزة المقدمة للاعتراف والإشادة بعمل أو قطعة أدبية.[1][2][3] وتقدم عادة إلى المؤلف. المنظمات معظم الجوائز الأدبية تأتي في حفل توزيع الجوائز. العديد من الجوائز تنظم مع منظمة واحدة (عادة ما تكون غير ربحية) كمقدم للجائزة ومنظمة أخرى كراعي مالي...

2008年夏季奥林匹克运动会丹麦代表團丹麦国旗IOC編碼DENNOC丹麥國家奧林匹克委員會及體育同盟網站www.dif.dk(丹麦文)2008年夏季奥林匹克运动会(北京)2008年8月8日至8月24日運動員84參賽項目16个大项旗手Joachim Olsen獎牌榜排名第30 金牌 銀牌 銅牌 總計 2 2 3 7 历届奥林匹克运动会参赛记录(总结)夏季奥林匹克运动会189619001904190819121920192419281932193619481952195619601964196819721976198019841...

Questa voce sull'argomento cestisti uruguaiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Sergio PisanoNazionalità Uruguay Altezza191 cm Peso92 kg Pallacanestro CarrieraNazionale 1961-1973 Uruguay Palmarès Campionati sudamericani ArgentoBrasile 1961 ArgentoUruguay 1971 Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Sergio Pisano Pe...

Traditional Japanese long knife used for filleting large fish Long maguro bōchō, used to filet tuna at the Tsukiji fish market A maguro bōchō in use at the Tsukiji fish market in Tokyo A maguro bōchō (Japanese: 鮪包丁, lit. tuna knife), or maguro kiri bōchō (鮪切り包丁, lit. tuna cutter), is an extremely long, highly specialized Japanese knife that is commonly used to fillet tuna, as well as many other types of large ocean fish. The maguro bōchō is a long knife with a blade ...

Fear of dead organisms This article is about the fear of dead things. For the fear of dying, see Death anxiety. For the 2014 film, see Necrofobia. Medical conditionNecrophobiaHuman skulls.SpecialtyPsychology Necrophobia is a specific phobia, the irrational fear of dead organisms (e.g., corpses) as well as things associated with death (e.g., coffins, tombstones, funerals, cemeteries). With all types of emotions, obsession with death becomes evident in both fascination and objectification.[...

President of Peru from 2018 to 2020 In this Spanish name, the first or paternal surname is Vizcarra and the second or maternal family name is Cornejo. Martín VizcarraOSP CYC GColIHVizcarra in 201860th President of PeruIn office23 March 2018 – 9 November 2020Prime MinisterMercedes AráozCésar VillanuevaSalvador del SolarVicente ZeballosPedro CaterianoWalter MartosVice PresidentFirst Vice PresidentVacantSecond Vice PresidentMercedes Aráoz(2018 – May 2020)Vacant(May – N...









![{\displaystyle \int _{a}^{b}f(x)d(sx)={\begin{cases}s\int _{s^{-1}b}^{s^{-1}a}f(x)dx=-s\int _{s^{-1}a}^{s^{-1}b}f(x)dx&(s<0),\\[5pt]s\int _{s^{-1}a}^{s^{-1}b}f(x)dx&(s>0).\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/463fe1dc1796c2468508dba43e8ff2f375de7ea7)


