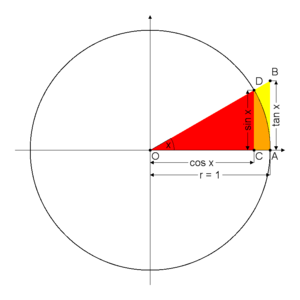
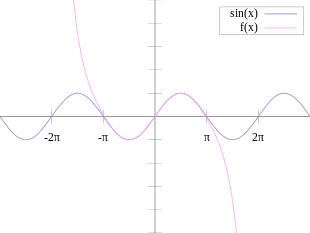
Seno (matematica)
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artyom BogomolovInformasi pribadiNama lengkap Artyom Igorevich BogomolovTanggal lahir 18 Juli 1992 (umur 31)Tinggi 1,83 m (6 ft 0 in)Posisi bermain GelandangInformasi klubKlub saat ini FC TyumenNomor 28Karier senior*Tahun Tim Tampi...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Perang Rusia-Turki (1877–1878)Bagian dari Krisis Timur BesarMonumen Plevna didekat tembok Kitai-gorodTanggal1877–1878LokasiBalkan, KaukasusHasil Kemenangan RusiaPerubahanwilayah Kongres BerlinKongres San Stefano Pembentukan Kepangeranan Bulgaria Kemerdekaan Rumania, Serbia dan MontenegroPihak terlibat Kekaisaran Rusia Romania Serbia Montenegro Bulgaria Kesultanan UtsmaniyahTokoh dan pemimpin Mikhail Skobelev Mikhail Loris-Melikov Joseph Gourko Ivan Lazarev Carol I dari Romania A...

SinunukanKecamatanPeta lokasi Kecamatan SinunukanNegara IndonesiaProvinsiSumatera UtaraKabupatenMandailing NatalPemerintahan • CamatSatruddin, S.HPopulasi • Total15,519 jiwa jiwaKode Kemendagri12.13.22 Kode BPS1202011 Luas23.663 km²Desa/kelurahan14 Sinunukan adalah sebuah kecamatan di Kabupaten Mandailing Natal, Sumatera Utara, Indonesia. Kecamatan ini termasuk kawasan Pantai Barat Sumatera Utara yang komoditas utama masyarakatnya adalah pertanian dan perkebunan ...

Cet article est une ébauche concernant la Grèce antique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. ÆgosthènesPrésentationType Polis, fortification, site archéologiquePériode Époque classique, époque hellénistiquePatrimonialité Site archéologique de Grèce (d)Site web odysseus.culture.gr/h/3/eh352.jsp?obj_id=12862LocalisationLocalisation Mándra-Idýllia GrèceCoordonnées 38° 08′&#...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Disambiguazione – Se stai cercando il film del 1981, vedi Hokusai Manga (film). MangaAlcuni degli schizzi contenuti nei volumiAutoreKatsushika Hokusai Data1814-1878 circa Tecnicaxilografia Ubicazionesconosciuta Hokusai manga (北斎漫画? Schizzi sparsi di Hokusai) è una raccolta di schizzi con vari soggetti, ad opera dell'artista giapponese Katsushika Hokusai. I soggetti dei disegni includono paesaggi, flora e fauna, scene di vita quotidiana e il soprannaturale. La parola manga nel ...

Italian luxury sports car manufacturer based in Maranello This article is about the automobile manufacturer. For other uses, see Ferrari (disambiguation). Ferraris redirects here. For the surname, see Ferraris (surname). Ferrari S.p.A.Headquarters in MaranelloCompany typePublic (S.p.A.)Traded asBIT: RACENYSE: RACEFTSE MIB componentEuro Stoxx 50 componentISINNL0011585146 IndustryAutomotiveFounded13 September 1939; 84 years ago (1939-09-13) in Modena, Italy (as ...

A solar-powered sign in Seria Energy Lab. Energy in Brunei is related to all of the type of energy and its related infrastructure used in Brunei.[1] Natural gas and diesel are used significantly in Brunei to generate domestic electricity, as well as gasoline and diesel to power its roads. Domestic supplies were undoubtedly still safe, but they were still susceptible to disturbances that would result in power outages and a lack of gasoline. To reduce the country's susceptibility and th...

Voce principale: Campionato mondiale di Formula 1 2011. Gran Premio del Canada 2011 846º GP del Mondiale di Formula 1Gara 7 di 19 del Campionato 2011 Data 12 giugno 2011 Nome ufficiale XLVIII Grand Prix du Canada Luogo Montréal Percorso 4,361 km / 2,71 US mi Circuito cittadino Distanza 70 giri, 305,27 km/ 189,7 US mi Clima Pioggia ad intervalli regolari, parzialmente asciutto nel finale della gara Note Gara sospesa per pioggia al 25º giro Risultati Pole position Giro più veloce Seb...

English composer Iain Bell during the rehearsals of his opera in Vienna October 2013 Iain Bell (born 1980) is an English composer whose output is predominantly of vocal works, namely opera, art song or orchestral song. Life and career Bell was born in Kingston Jamaica. His first opera, A Harlot's Progress, to a libretto by Peter Ackroyd, premiered on 13 October 2013 at the Theater an der Wien in Vienna, conducted by Mikko Franck and directed by Jens-Daniel Herzog. The cast included Marie McLa...

Al-Quwa Al-JawiyaCalcio Al-Soqoor, Al-Areeq Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori socialiblu,bianco Dati societariCittàRusafa Nazione Iraq ConfederazioneAFC Federazione IFA CampionatoPrima Lega Fondazione1931 Proprietario Ministero iracheno della difesa Presidente Anwar Hamad Ameen Allenatore Ayoub Od Barcham StadioAl-Quwa Al-Jawiya(10 000 posti) PalmarèsTitoli nazionali7 campionati iracheni Trofei nazionali4 Coppe d'Iraq2 Supercoppe de'Iraq Trofei interna...

Passenger railway station in Israel Hod Hasharon Sokolov railway stationתחנת הרכבת הוד השרון—סוקולובIsrael RailwaysTrain on platform no. 1 preparing to leave towards HaRishonim station (Before the relocation of the line to the Southern Ayalon railway and its extension to Ra'anana)General informationLocationHod HaSharon,IsraelCoordinates32°10′12″N 34°54′09″E / 32.17000°N 34.90250°E / 32.17000; 34.90250Line(s)Sharon RailwayPlatforms2...

Serie ASkuad Juventus musim 1959–60Musim1959–60JuaraJuventusGelar juara ke-11DegradasiPalermoAlessandriaGenoaEuropean CupJuventusCup Winners' CupFiorentinaInter-Cities Fairs CupInternazionaleRomaJumlah pertandingan306Jumlah gol792 (2,59 per pertandingan)Pencetak golterbanyakOmar Sivori(28 gol)← 1958–59 1960–61 → Serie A musim 1959–1960 dimenangkan oleh Juventus. AlessandriaAtalantaBariBolognaFiorentinaGenoaSampdoriaInternazionaleMilanJuventusVicenzaLazioRomaNapoliPadovaPale...

Saalumarada ThimmakkaThimmakka pada tahun 2011Lahir1910/1911 (umur 112–113)[1][2][3]Gubbi Taluk, Tumkur,Kerajaan Mysore(kini Karnataka, India)[4]PekerjaanPegiat lingkunganSuami/istriBikaalu ChikkaiahAnak1PenghargaanPadma Shri (2019) Saalumarada Thimmakka, juga dikenal dengan nama Aalada Marada Timakka, adalah seorang pegiat lingkungan dari negara bagian Karnataka di India yang dikenal karena telah menanam dan merawat 385 pohon beringin di sepanjang jala...

معركة تشرنيغوف جزء من الغزو الروسي لأوكرانيا 2022 معلومات عامة التاريخ 24 فبراير 2022 – الآن (2 سنوات، و4 شهور، و4 أسابيع) البلد أوكرانيا الموقع تشرنيغوف، أوكرانيا51°29′38″N 31°17′41″E / 51.493888888889°N 31.294722222222°E / 51.493888888889; 31.294722222222 النتيجة مستمرة المتحاربون &#...

Canadian politician Libby DaviesCMDavies at the 2006 New Democratic Party federal convention in Quebec CityDeputy Leader of the New Democratic PartyIn office2007 – August 4, 2015Serving with Thomas Mulcair until 2012, then Megan Leslie and David Christopherson from 2012 to 2015LeaderJack LaytonThomas MulcairPreceded byBill BlaikieSucceeded byDavid ChristophersonShadow Minister for HealthIn officeMay 26, 2011 – January 22, 2015LeaderJack LaytonNycole TurmelThomas ...

بيلاروس أو روسيا البيضاء (بالبيلاروسية: Беларусь وتلفظ [bʲɛ.ɫa.rusʲ]) دولة داخلية في أوروبا الشرقية تحدها الدول التالية باتجاه عقارب الساعة روسيا إلى الشمال الشرقي وأوكرانيا إلى الجنوب وبولندا إلى الغرب وليتوانيا ولاتفيا إلى الشمال الغربي. عاصمتها مينسك ومن المدن الرئيسية ا...

Detective Conan: Zero's Tea TimeGambar sampul manga volume pertama名探偵コナン ゼロの日常(Meitantei Conan: Zero no Nichijou) MangaPengarangTakahiro AraiPenerbitShogakukanPenerbit bahasa InggrisSG Shogakukan AsiaMajalahWeekly Shōnen SundayDemografiShōnenTerbit9 Mei 2018 – 25 September 2019Volume5 (Daftar volume) Portal anime dan manga Detective Conan: Zero's Tea Time (Jepang: 名探偵コナン ゼロの日常code: ja is deprecated , Hepburn: Meitantei Konan Zero No Ni...








![{\displaystyle [-1;+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90f1555bbff659d4d69b48a914890f5df95f2a0)









































![{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














