Risonanza orbitale
|
Read other articles:

Artikel ini bukan mengenai David Maulana. Septian David Maulana Informasi pribadiNama lengkap Septian David MaulanaTanggal lahir 1 September 1996 (umur 27)Tempat lahir Semarang, Jawa TengahTinggi 1,74 m (5 ft 8+1⁄2 in)Posisi bermain Attacking midfielderInformasi klubKlub saat ini PSIS SemarangNomor 29Karier junior0000–2012 SSB Bhaladika2012–2015 Deportivo IndonesiaKarier senior*Tahun Tim Tampil (Gol)2015–2019 Mitra Kukar 71 (16)2019– PSIS Semarang 84 (15)Tim ...

Hodag yang tertangkap oleh Eugene Shephard, pada tahun 1893 Hodag adalah hewan mitos atau kriptid dari negara bagian Wisconsin, Amerika serikat. Kisah tentang mahluk ini terutama berkembang disekitar kota Rhinelander di sebelah utara Wisconsin, di mana diceritakan sering ada penampakan mahluk kriptid ini. Hodag juga diceritakan dalam cerita Paul Bunyan. Awal mula Pada 1893, surat kabar memberitakan penemuan seekor hodag di Rhinelander, Wisconsin. Hodag diceritakan memiliki kepala kodok, wajah...

President of Kenya from 1988 to 2002 This article is about a person whose name includes a patronymic. As such, this person should normally be referred to by their given name, Daniel. His ExcellencyDaniel arap MoiCGHMoi in 19792nd President of KenyaIn office22 August 1978 – 30 December 2002Vice President Mwai Kibaki Josephat Karanja George Saitoti Musalia Mudavadi Preceded byJomo KenyattaSucceeded byMwai KibakiChairperson of the OAUIn office24 June 1981 – 6 June 1983P...

Questa voce sugli argomenti circondari della Germania e Baviera è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Circondario di Weilheim-SchongaucircondarioLandkreis Weilheim-Schongau LocalizzazioneStato Germania Land Baviera Distretto Alta Baviera AmministrazioneCapoluogoWeilheim in Oberbayern TerritorioCoordinatedel capoluogo47°50′N 11°09′E / 47.833333°N 11.15°E47.833333; 11.15 (Circondario di Weilheim-Schongau...

1983 film directed by Shōhei Imamura For the 1958 film, see The Ballad of Narayama (1958 film). The Ballad of NarayamaPoster for Ballad of Narayama (1983)Directed byShōhei ImamuraWritten byShōhei ImamuraBased on楢山節考 (Narayama-bushi Kō)by Shichirō FukazawaProduced byGoro Kusakabe Jiro TomodaStarringKen Ogata Sumiko Sakamoto Takejo Aki Tonpei Hidari Seiji Kurasaki Kaoru Shimamori Ryutaro Tatsumi Junko Takada Nijiko Kiyokawa Mitsuko BaishoCinematographyMasao TochizawaEdited byHajime...

Beruang cokelat eurasia Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Carnivora Famili: Ursidae Genus: Ursus Spesies: U. arctos Subspesies: U. arctos arctos Nama trinomial Ursus arctos arctosLinnaeus, 1758 Beruang cokelat eurasia (Ursus arctos arctos) adalah subspesies dari beruang cokelat yang dapat ditemukan di utara Eurasia. Beruang cokelat Eurasia juga dikenal sebagai beruang cokelat/beruan...

Football match1969 European Cup finalThe match programme coverEvent1968–69 European Cup Milan Ajax 4 1 Date28 May 1969VenueSantiago Bernabéu, MadridRefereeJosé María Ortiz de Mendíbil (Spain)Attendance31,782← 1968 1970 → Advertising poster for the game The 1969 European Cup final was a football match played at the Santiago Bernabéu Stadium in Madrid on 28 May 1969 between AC Milan of Italy and Ajax of the Netherlands, to determine the champions of the 1968–69 European Cu...

Artikel ini bukan mengenai Final Liga Negara UEFA 2023, pertandingan final Liga Negara UEFA. Babak final Liga Negara UEFA 2023Finaleronde UEFA Nations League 2023 (Belanda)Informasi turnamenTuan rumahBelandaJadwalpenyelenggaraan14–18 Juni 2023Jumlahtim peserta4Tempatpenyelenggaraan2 (di 2 kota)Hasil turnamenJuara Spanyol (gelar ke-1)Tempat kedua KroasiaTempat ketiga ItaliaTempat keempat BelandaStatistik turnamenJumlahpertandingan4Jumlah gol14 (3,5 per pertandin...

2020 anti-racism protests in New Zealand George Floyd protests in New ZealandPart of George Floyd protestsDate1 June 2020 – 14 June 2020LocationNew ZealandCaused by Police brutality Institutional racism against Māori Reaction to the murder of George Floyd Solidarity with concurrent protests in the United States Cities in New Zealand in which a protest with about 100 or more participants was held (vte) Shortly after protests seeking justice for George Floyd, an African-American who was murd...

Berkeley SETI Research CenterLogoFormation2012; 12 years ago (2012)PurposeDetermine the prevalence of intelligent life in the universeHeadquartersBerkeley, CaliforniaDirectorAndrew SiemionParent organizationUniversity of California, BerkeleyWebsiteseti.berkeley.edu Screen shot of the screensaver for SETI@home, a distributed computing project in which volunteers donate idle computer power to analyze radio signals for signs of extraterrestrial intelligence. This article is one...
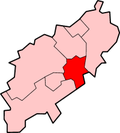
Former borough in England Non-metropolitan district and borough in EnglandBorough of WellingboroughNon-metropolitan district and boroughShown within NorthamptonshireSovereign stateUnited KingdomConstituent countryEnglandRegionEast MidlandsCeremonial countyNorthamptonshireAdmin. HQWellingboroughGovernment • TypeBorough Council of Wellingborough • Leadership:Alternative - Sec.31 • Executive: • MPs:Peter Bone • Leader of the ...

Carl Ernst Otto Kuntze 1843 - 1907 Carl Ernst Otto Kuntze (23 June 1843–27 January 1907) adalah botanis Jerman. Standar singkatan penulis Kuntze digunakan untuk mengindikasikan orang ini ketika mengutip sebuah nama botani.[1] Artikel biografi Barnhart, John Hendley (1913). Otto Kuntze. Bulletin of the Charleston Museum. 9. hlm. 65–68. Urban, Ignaz (1902). Symbolae Antillanae (dalam bahasa Latin) (3): 70. . Hemsley, W. B. (1907). Dr. Otto Kuntze. Kew Bulletin of Mis...

Weekly Franco-Belgian comics magazine SpirouSpirou No. 1 (21 April 1938)Front cover by Rob-Vel.Publication informationPublisherDupuisScheduleWeeklyPublication date21 April 1938 – presentMain character(s)Spirou Spirou[a] (French: Le Journal de Spirou) is a weekly Belgian comics magazine published by the Dupuis company since April 21, 1938. It is an anthology magazine with new features appearing regularly, containing a mix of short humor strips and serialized features, of which the mo...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) الدوري الإيطالي الدرجة الثانية 1974–75 تفاصيل الموسم الدوري الإيطالي الدرجة الثانية النسخة 43 ال...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Musical form and a music genre typical of Spain and parts of Latin America This article is about the dance. For other uses, see Fandango (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2012) (Learn how and when to remove this message) Fandango is a lively partner dance originating in Portugal and Spain, usually in triple meter, tradition...

19th-century American entertainers who first performed minstrel shows This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Virginia Minstrels – news · newspapers · books · scholar · JSTOR (June 2018) (Learn how and when to remove this message) Detail from cover of The Celebrated Negro Melodies, as Sung by the Vir...

Money FlowerPoster promosiJudul asli돈꽃 GenreAsmara, Bisnis, DramaPembuatLee Jae-dongDitulis olehLee Myung-heeSutradaraKim Hee-wonPemeranJang HyukPark Se-youngJang Seung-joNegara asalKorea SelatanBahasa asliKoreaJmlh. episode24ProduksiProduser eksekutifNam Gung-kyeon[1]Durasi60 menitRumah produksiUFO Production[1]DistributorMBCRilis asliJaringanMBCRilis () –2018 (2018) Money Flower (Hangul: 돈꽃; RR: Donkkot) adalah serial televisi ...

Women's national association football team representing Malta This article is about the women's team. For the men's team, see Malta national football team. MaltaAssociationMalta Football AssociationConfederationUEFA (Europe)Head coachManuela TesseCaptainEmma LipmanMost capsDorianne Theuma (116)Top scorerDorianne Theuma (26)Home stadiumCentenary StadiumFIFA codeMLT First colours Second colours FIFA rankingCurrent 87 (14 June 2024)[1]Highest74 (August 2003)Lowest115 (October 2007)First ...

约公元前6世纪的地中海。黄色标签为腓尼基人建立的城市,红色为希腊人建立的城市,灰色为其他民族建立的城市。 古代殖民地是指古代地中海地区的文明建立的海外殖民地,大多与母城邦(metropolis,英语中大都市一词即来源于此)领土不接壤的殖民城邦的形式。殖民城市与母城市之间的联系依然十分紧密,但与近代的殖民主义不同的是,这种联系并不以母城市直接控制�...







