Numero stella octangulare

124 palline magnetiche disposte a formare una stella octangula. 124 è un numero stellato octangulare

In teoria dei numeri, un numero stella octangulare è un numero figurato che rappresenta una stella octangula.

La formula per l' $n$ -simo numero stella octangulare è:

n(2n^{2}-1).

^[1]

I primi numeri stella octangulari sono: 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, 2651, 3444^[2].

Proprietà matematiche

L' $n$ -esimo numero stella octangulare può essere espresso come la somma dell' $n$ -esimo numero ottaedrico e di 8 volte l' $(n-1)$ -esimo numero tetraedrico.

Gli unici numeri stella octangulari ad essere anche quadrati perfetti sono 1 e 9653449 (3107²), rispettivamente il 1º e il 169º dei numeri di questa forma^[3]. Ciò è stato dimostrato considerando che la curva ellittica che descrive i numeri allo stesso tempo stella octangulari e quadrati,

m^{2}=n(2n^{2}-1),

può essere posta nell'equivalente forma di Weierstrass

x^{2}=y^{3}-2y

sostituendo $2m$ con $x$ e $2n$ con $y$ . Dato che $n$ e $2n^{2}-1$ , i due fattori di $m^{2}$ , sono primi tra loro, devono essere anch'essi quadrati.

Ora, ponendo $X={\frac {m}{\sqrt {n}}}$ e $Y={\sqrt {n}}$ , si ha

X^{2}=2Y^{4}-1.

^[3]

Un teorema di Siegel afferma che ogni equazione ellittica ha solo un numero finito di soluzioni intere, e nel 1942 il matematico Wilhelm Ljunggren ha pubblicato una complessa dimostrazione del fatto che le due soluzioni note siano le uniche. Per questo, l'ultima equivalenza è anche nota come equazione di Ljunggren^[4] Louis J. Mordell congetturò che tale dimostrazione potesse essere semplificata, come in effetti è poi avvenuto per merito di più matematici.^[3]^[5]^[6].

Note

^ John Conway, Richard K. Guy, The Book of Numbers, Springer, 1996, p. 51, ISBN 978-0-387-97993-9..
^ (EN) Sequenza A007588, su On-Line Encyclopedia of Integer Sequences, The OEIS Foundation.
^ ^a ^b ^c Samir Siksek, Descents on Curves of Genus I (PDF) ^{[collegamento interrotto]}, in Tesi di PhD, Università di Exeter, 1995, pp. 16–17.
^ Wilhelm Ljunggren, Zur Theorie der Gleichung x² + 1 = Dy⁴, in Avh. Norske Vid. Akad. Oslo. I., vol. 1942, n. 5, 1942, p. 27..
^ Ray Steiner, Nikos Tzanakis, Simplifying the solution of Ljunggren's equation X² + 1 = 2Y⁴ (PDF), in Journal of Number Theory, vol. 37, n. 2, 1991, pp. 123–132. URL consultato il 24 agosto 2012 (archiviato dall'url originale il 4 marzo 2016).
^ Konstantinos A. Draziotis, The Ljunggren equation revisited, in Colloquium Mathematicum, vol. 109, n. 1, 2007, pp. 9–11.

Collegamenti esterni

(EN) Eric W. Weisstein, Numero stella octangulare, su MathWorld, Wolfram Research.

V · D · M Numeri figurati
Numeri poligonali	Numero triangolare · Numero quadrato · Numero pentagonale · Numero esagonale · Numero ettagonale · Numero ottagonale · Numero ennagonale · Numero decagonale · Numero oblungo · Numero poligonale centrale
Numeri poligonali centrati	Numero triangolare centrato · Numero quadrato centrato · Numero pentagonale centrato · Numero esagonale centrato · Numero ettagonale centrato · Numero ottagonale centrato · Numero ennagonale centrato · Numero decagonale centrato · Numero stellato
Numeri poliedrici	Numero tetraedrico · Numero piramidale quadrato · Numero piramidale pentagonale · Numero piramidale esagonale · Numero piramidale ettagonale · Numero ottaedrico · Numero ottaedrico troncato · Numero stella octangulare · Numero cubico · Numero cubico centrato
Numeri politopici	Numero pentatopico · Numero ipercubico
Altro	Teorema di Fermat sui numeri poligonali

Portale Matematica: accedi alle voci di Wikipedia che trattano di Matematica

Read other articles:

Geometra

Disambiguazione – Se stai cercando lo studioso della geometria, vedi geometria. Il geometra (abbreviato geom.) è il professionista che misura, valuta e progetta opere pubbliche o private di modesta entità. Può inoltre progettare opere di modesta entità in cemento armato. Il suo percorso di studi gli consente di stimare la proprietà privata, costruita o non, la superficie e il sottosuolo oltre che operare nel settore urbanistico, della direzione dei lavori e della sicurezza. La prepara...

Wolfgang Ketterle

Wolfgang Ketterle Lahir21 Oktober 1957 (umur 66)Heidelberg, Jerman BaratTempat tinggalJermanAmerika SerikatKebangsaanJermanAlmamaterHeidelberg Lembaga Max Planck untuk Optika Kuantum di Garching Universitas Teknik MünchenSuami/istriGabriele SauerAnakJonas, Johanna, HolgerPenghargaan Penghargaan Nobel Fisika (2001)Karier ilmiahBidangFisika Bahan yang DipadatkanInstitusiHeidelberg MITPembimbing doktoralHerbert Walther dan Hartmut Figger Situs webhttp://web.mit.edu/physics/facultyandstaff...

Honor Concept

Part of the United States Naval Academy Honor Program The Honor Concept[1] and Honor Treatise are parts of the United States Naval Academy's Honor Program. Similar to the Cadet Honor Codes of the United States Military Academy and United States Air Force Academy, the Concept formalizes the requirement for midshipmen to demonstrate integrity while refusing to lie, cheat or steal.[2] The Treatise adopts the use of first-person point of view, becoming a personal call to obey the ...

Jean-Michel Boucheron (homme politique, 1946)

Pour les articles homonymes, voir Jean-Michel Boucheron. Jean-Michel Boucheron Fonctions Secrétaire d’État chargé des Collectivités territoriales 10 mai 1988 – 22 juin 1988(1 mois et 12 jours) Élection 21 juin 1988 Premier ministre Michel Rocard Gouvernement Michel Rocard I Prédécesseur Yves Galland (Ministre délégué aux Collectivités locales) Successeur Jean-Michel Baylet Député français 23 juin 1988 – 1er avril 1993(4 ans, 9 mois et 9 jours) Cir...

Coppa Mercosur 1998

La Coppa Mercosur 1998 fu la prima edizione del torneo sudamericano di calcio e ebbe come campione il Palmeiras, club brasiliano della città di San Paolo. L'edizione 1998 contò sei squadre argentine, sette brasiliane, tre cilene, due Paraguaiane e due Uruguaiane. Indice 1 Formula 2 Trasmissione 3 Prima fase 3.1 Gruppo A 3.2 Gruppo B 3.3 Gruppo C 3.4 Gruppo D 3.5 Gruppo E 4 Seconda fase 4.1 Quarti di finale 4.2 Semifinali 4.2.1 Andata 4.2.2 = Ritorno 4.3 Finale 4.3.1 Andata 4.3.2 Ritorno 5 C...

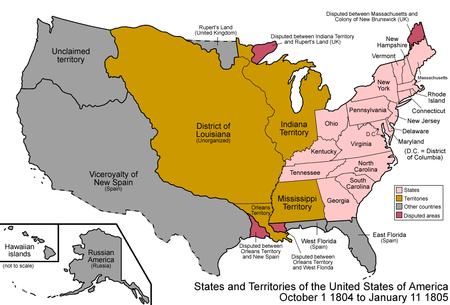
District of Louisiana

Territory of the USA between 1804-1805 District of LouisianaIncorporated and unorganized territory of the United States1804–1805A map of the District of LouisianaCapitalSt. LouisGovernmentGovernor • 1804–1805 William Henry Harrison History • Established October 1 1804• Organized July 4 1805 Preceded by Succeeded by Louisiana Purchase Territory of Louisiana The District of Louisiana, or Louisiana District, was an official and temporary United States governmen...

Copa BBVA Colsanitas 2011 - Doppio

Copa BBVA Colsanitas 2011Doppio Sport Tennis Vincitori Edina Gallovits-Hall Anabel Medina Garrigues Finalisti Sharon Fichman Laura Pous Tió Punteggio 2–6, 7–6(6), [11–9] Tornei Singolare Singolare (q) Doppio Doppio 2010 2012 Voce principale: Copa BBVA Colsanitas 2011. Il doppio della Copa BBVA Colsanitas 2011 è stato un torneo di tennis facente parte del WTA Tour 2011. Gisela Dulko e Edina Gallovits-Hall erano le detentrici del titolo, ma Dulko non ha partecipato. Gallovits-Ha...

Breckin Meyer

American actor Breckin MeyerMeyer in 2011Born (1974-05-07) May 7, 1974 (age 49)Minneapolis, Minnesota, U.S.Occupations Actor comedian writer producer drummer Years active1983–presentSpouse Deborah Kaplan (m. 2001; div. 2014)Children2 Breckin Meyer[1] (born May 7, 1974) is an American actor, comedian, writer, and producer. He is best known for his roles in films such as Clueless (1995), The Craft (1996), Road Trip (2000), ...

Lindenstraße (soap opera)

Questa voce sull'argomento fiction televisive tedesche è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. LindenstraßeIl logo della fiction utilizzato dal 1985 al 2015Titolo originaleLindenstraße PaeseGermania Anno1985-2020 Formatoserial TV Generesoap opera Stagioni1 Puntate1.758[1][2][3][4] Durata29 min. (ep.) Lingua originaleTedesco CreditiIdeatoreHans W. Geißendörfer RegiaHerwig FischerDominikus Probst George Moorse...

Eosinopteryx

Extinct genus of dinosaurs EosinopteryxTemporal range: Late Jurassic, 160 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Life restoration Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Theropoda Family: †Anchiornithidae Genus: †EosinopteryxGodefroit et al., 2013 Type species †Eosinopteryx brevipennaGodefroit et al., 2013 Eosinopteryx is an extinct genus of theropod dinosaurs known to the Late Jurassic epoch of C...

Новотитаровское сельское поселение

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Stato canaglia

Stati Uniti Stati considerati Stati Canaglia dagli Stati Uniti Stati considerati Stati canaglia dagli Stati Uniti:[1][2] Afghanistan Corea del Nord[3] Cuba Iran[2] Nicaragua Siria[2] Venezuela Stati considerati in passato Stati canaglia dagli Stati Uniti: Iraq Jugoslavia Libia Sudafrica Sudan Yemen del Sud Stato canaglia (rogue state...

List of cemeteries in Russia

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of cemeteries in Russia – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove th...

فريق كريس ساكتي

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) فريق كريس ساكتي الإنشاء 2011 تعديل مصدري - تعديل فريق كريس ساكتي للاستعراض الجوي، (Kris Sakti). (بالإنجليز...

Пиранези, Джованни Баттиста

У этого термина существуют и другие значения, см. Пиранези. Джованни Баттиста Пиранезиитал. Giovanni Battista Piranesi Франческо Пиранези. Портрет Джованни Баттиста Пиранези. 1779. Офорт Дата рождения 4 октября 1720(1720-10-04) Место рождения Мольяно-Венето или Венеция Дата смерти 9 нояб�...

دوري جزر فارو الممتاز 1997

دوري جزر فارو الممتاز 1997 تفاصيل الموسم دوري جزر فارو الممتاز النسخة 56 البلد جزر فارو التاريخ بداية:25 أبريل 1997 نهاية:4 أكتوبر 1997 المنظم اتحاد جزر فارو لكرة القدم البطل بي36 توشهافن مباريات ملعوبة 90 عدد المشاركين 10 دوري جزر فارو الممتاز 1996 دور...

Австрийский почтово-телеграфный музей

Австрийский почтово-телеграфный музейнем. Österreichisches Post- und Telegraphenmuseum Эмблема музея на обложке изданияк его 70-летнему юбилею[1] Дата основания 1891 Адрес Mariahilfer Straße 212, Vienna, Austria Сайт Сайт Технического музея Австрийский почтово-телеграфный музей (нем. Österreichisches Post- und Te...

Richard Shelley

For the diplomat and grand prior of the Knights of Saint John, see Richard Shelley (grand prior). This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2024) (Learn how and when to remove this message) Marshalsea Notable prisoners Sir Francis Barrington Edmund Bonner Henry Chettle Richard Cox Robert Culliford Robert Daborn...

Willis Tower

Skyscraper in Chicago, Illinois Willis TowerWillis Tower as seen from Lake Michigan in April 2019Former namesSears Tower (1973–2009)Record heightTallest in the world from 1973 to 1998[I]Preceded byWorld Trade CenterSurpassed byPetronas Towers[4]General informationStatusCompletedTypeOffice, observation, communicationArchitectural styleInternationalLocation233 S. Wacker DriveChicago, Illinois 60606United StatesCoordinates41°52′44″N 87°38′09″W / 41.8789°N 87....

Var's 5th constituency

Constituency of the National Assembly of France 5th constituency of VarinlineConstituency of the National Assembly of FranceVar's 5th Constituency shown within the VarDeputyJulie LechanteuxRNDepartmentVarCantonsFréjus, Le Muy, Saint-RaphaëlRegistered voters96,236[1] Politics of France Political parties Elections Previous Next The 5th constituency of the Var (French: Cinquième circonscription du Var) is a French legislative constituency in the Var département. Like the other 576 Fr...

/profillengkap.com/index.php/article/Ochakiv

/profillengkap.com/index.php/article/1988–89 Newport County A.F.C. season

Carmel Valley, San Diego

Tyrese Gibson

Something New (Axwell & Ingrosso song)

Suitland High School

Abraham Lincoln (relief by Schwarz)