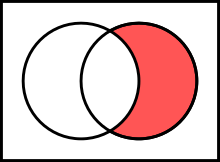
Komplemen (teori himpunan)
|
Read other articles:

Afrika Barat Daya JermanDeutsch-Südwestafrika1884–1915 Bendera Lambang Afrika Barat Daya Jerman (merah), koloni Jerman lain berwarna biruStatusKoloniIbu kotaWindhoek (dari 1891)Gubernur • 1898-1905 Theodor von Leutwein• 1905-1907 Friedrich von Lindequist• 1907-1910 Bruno von Schuckmann• 1910-1915 Theodor Seitz Era SejarahPerebutan Afrika• Didirikan 7 Agustus 1884• Genosida 1904-1907• Dibubarkan 9 Juli 1915• Perjanjian Versailles ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Hanacaraka – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2023) Hanacaraka adalah sebutan untuk sejumlah aksara serumpun yang terutama digunakan di pulau Jawa dan Bali.[butuh rujukan] Is...

Pour les articles homonymes, voir Brunhes. Jacques Brunhes Fonctions Secrétaire d'État au Tourisme 23 octobre 2001 – 6 mai 2002 (6 mois et 13 jours) Président Jacques Chirac Premier ministre Lionel Jospin Gouvernement Jospin Prédécesseur Michelle Demessine Successeur Gilles de Robien Maire de Gennevilliers 22 septembre 1987 – octobre 2001 (14 ans et 13 jours) Réélection 1989, 1995 Prédécesseur Lucien Lanternier Successeur Jacques Bourgoin Conseiller général...

Dominion Pakistanمملکتِ پاکستانপাকিস্তান অধিরাজ্য1947–1971[1] Bendera Lambang (1947-1955) Semboyan: Iman, Ittehad, Tanzeemایمان ، اتحاد ، تنظیمKeyakinan, Persatuan, DisiplinLagu kebangsaan: Qaumī Tarāna (1954–1956)قومی ترانہPakistan pada 1956Ibu kotaKarachiBahasa yang umum digunakanInggrisa, Urdub, Bengalic,PemerintahanMonarki konstitusional parlementer federalPenguasa monarki • 1...

For other places with the same name, see Zwolle (disambiguation). Not to be confused with Zvolen or Zwolen. City and municipality in Overijssel, NetherlandsZwolleCity and municipalitySassenstraatGrote MarktMuseum de FundatieLuttekestraatBinnenstad FlagCoat of armsLocation in OverijsselZwolleLocation within the NetherlandsShow map of NetherlandsZwolleLocation within EuropeShow map of EuropeCoordinates: 52°31′N 6°6′E / 52.517°N 6.100°E / 52.517; 6.100CountryNethe...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Arabic calligrapher and manuscript illuminator (d. 1022) Ibn al-BawwabIbn al-Bawwab script seen here is the earliest existing example of a Qur'an written in a cursive script, Chester Beatty LibraryBorn975 or 1000IraqDied1022 or 1031BaghdadKnown forIslamic calligraphyMovementNaskh Thuluth muhaqqaq Wikimedia Commons has media related to Ibn al-Bawwab. Ibn al-Bawwāb (Arabic: إِبْن ٱلْبَوَّاب), also known as Ali ibn-Hilal, Abu'l-Hasan, and Ibn al-Sitri, was an Arabic calligra...

Generic Dutch term for administrative divisions In the Netherlands, the term public body (a literal translation from the Dutch term openbaar lichaam) is the general denomination for administrative divisions within the Dutch state, such as the central government, a province, a municipality or a water board. These types of political entities are defined by the Constitution of the Netherlands.[1] In addition, Article 134 of the constitution provides for the definition of other public bod...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Sports complex Queenstown Events CentreView of the Queenstown Events Centre BuildingQueenstown Events CentreLocation within New ZealandFormer namesJohn Davies Oval, Davies ParkLocationJoe O'Connell Drive, Frankton, Queenstown, New ZealandCoordinates45°0′58″S 168°44′18″E / 45.01611°S 168.73833°E / -45.01611; 168.73833OwnerQueenstown-Lakes District CouncilOperatorLakes LeisureCapacity19,000[1]SurfaceGrassTenantsOtago Rugby Football Union, Highlanders,...

Demografi MeksikoPiramida penduduk Meksiko pada 2020Populasi129.150.971[1]Tingkat pertumbuhan1,9% (2015)[2]Tingkat kelahiran14,8 kelahiran/1.000 penduduk (per. 2022)Tingkat kematian6,5 kematian/1.000 penduduk (per. 2022)Harapan hidup76,66 tahun • laki-laki73,84 tahun • perempuan79,63 tahun (per. 2012)Tingkat kesuburan1,63 kelahiran anak/wanita (per. 2020)Tingkat kematian bayi16,77 kematian/1.000 kelahiran hidupTingkat migrasi bersih−1,64 migran/1.000 ...

Census-designated place in Hawaii, United States Census-designated place in Hawaii, United StatesEast HonoluluCensus-designated placeCoordinates: 21°17′20″N 157°43′2″W / 21.28889°N 157.71722°W / 21.28889; -157.71722Country United StatesState HawaiiCountiesHonoluluArea[1] • Total34.45 sq mi (89.24 km2) • Land23.01 sq mi (59.58 km2) • Water11.45 sq mi (29.65 km2...

British politician (1819–1900) For other people with the same name, see William Brooks (disambiguation). SirWilliam Cunliffe BrooksBt DL JPThe Golden Pippen. Caricature by Spy published in Vanity Fair in 1879.Born30 September 1819Died9 June 1900Glen Tanar, Aboyne, AberdeenshireAlma materRugbySt John's College, CambridgeInner TempleOccupationsBarristerBankerPoliticianSpouseJane Elizabeth Orrell Sir William Cunliffe Brooks, 1st Baronet, DL JP (30 September 1819 – 9 June 1900) was a...

Macarena Montesinos Secretaria General del Partido Popular en el Congreso de los Diputados Actualmente en el cargo Desde el 30 de noviembre de 2023Presidente Alberto Núñez Feijóo Coordinadora de Comisiones del Partido Popular en el Congreso de los Diputados Actualmente en el cargo Desde el 3 de abril de 2022Presidente Alberto Núñez Feijóo Diputada en las Cortes Generalespor Alicante Actualmente en el cargo Desde el 21 de mayo de 2019 2 de abril de 2004-13 de enero de 2016 Diputada de la...

Questa voce o sezione sull'argomento società calcistiche israeliane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sull'argomento società calcistiche israeliane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Beitar Tel Aviv Bat YamCalcio Segni distintiviUniformi di gara Casa Trasferta Colori social...

Disambiguazione – Se stai cercando l'omonima rivista, vedi Letteratura (rivista). Scultura commemorante Johannes Gutenberg, Berlino Omero, Iliade, Libro VIII, versi 245-253 - da un manoscritto greco di fine V secolo o inizio VI secolo. La letteratura di una certa lingua è l'insieme delle opere scritte e pervenute fino al presente. Tale definizione non è affatto scontata e va precisata sotto diversi aspetti. Da un lato, le definizioni che sono state date del termine, sensibili a diverse i...

American politician His ExcellencyRobert Daniell18th Governor of South CarolinaIn office1716–1717MonarchGeorge IPreceded byCharles CravenSucceeded byRobert Johnson3rd Deputy Governor of North CarolinaIn office1704–1705Preceded byHenderson Walker (Acting)Succeeded byThomas Cary Personal detailsBornApril 20, 1646Cardigan, Wales[citation needed]DiedMay 1, 1718 (aged 71–72)Daniel Island (present-day Charleston, South Carolina)Resting placeCharleston, South CarolinaSpouse(s)...

Huitième circonscription du Val-d'Oise Carte de la circonscription.Géographie Pays France Région Île-de-France Département Val-d'Oise Subdivisions Cantons 4 Communes 5 Représentation Député Carlos Martens Bilongo Législature XVIe (Cinquième République) Groupe parlementaire LFI Autres informations Population 108 050 hab. (1999) Date de création 24 novembre 1986 modifier La huitième circonscription du Val-d'Oise est l'une des dix circonscriptions législatives françaises que...

この項目では、中国思想における天について説明しています。その他の用法については「天 (曖昧さ回避)」をご覧ください。 天金文で記された「天」中国語 天 文字通りの意味heaven(s)発音記号標準中国語漢語拼音tiānウェード式t'ien1IPA[ti̯ɛn]呉語ローマ字thi (T1)贛語ローマ字tien1粤語粤拼tin1閩南語閩南語白話字thiⁿ中古音中古音tʰen上古音鄭張/*qʰl'iːn/日本語漢字 天 篆�...