Teorema Cantor
|
Read other articles:

Rok dengan gampai di jahitannya. Gampai atau Godet ( /ɡoʊˈdeɪ/ atau /ɡoʊˈdɛt/ ) [1] adalah potongan kain tambahan berbentuk bidang melingkar yang dijadikan pakaian, biasanya gaun atau rok .[2] Penambahan gampai menyebabkan pakaian tersebut melebar, sehingga menambah lebar dan volume . Penggunaan gampai yang paling populer adalah pada rok dalam.[3] Menambahkan gampai pada pakaian juga memberikan jangkauan gerak yang lebih luas bagi pemakainya. [4] Refere...
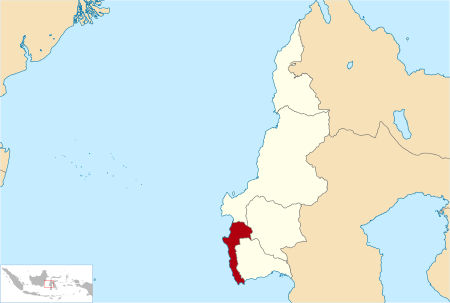
Peta Kabupaten Majene di Sulawesi Barat Berikut adalah daftar kecamatan dan kelurahan di Kabupaten Majene, Provinsi Sulawesi Barat, Indonesia. Kabupaten Majene terdiri dari 8 kecamatan, 20 kelurahan, dan 62 desa. Pada tahun 2017, jumlah penduduknya mencapai 166.505 jiwa dengan luas wilayah 947,84 km² dan sebaran penduduk 175 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Majene, adalah sebagai berikut: Kode Kemendagri Kecamatan Jumlah Kelurahan Jumlah Desa Statu...

The COVID-19 pandemic in Thailand began with the identification of the first case in the country on 13 January 2020, and has been ongoing since then. Timeline January 2020 One of the earliest announcements on the disease in Thailand, concerning only those who had been travelling from China On 13 January, the Ministry of Public Health announced the first confirmed case, a 61-year-old Chinese woman who is a resident of Wuhan. She had not visited the Huanan Seafood Wholesale Market, but was not...

Questa voce sull'argomento metropolitana di Lisbona è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Alto dos Moinhos Stazione dellametropolitana di Lisbona GestoreMetropolitano de Lisboa Inaugurazione1988 StatoIn uso Linealinea Blu Tipologiastazione sotterranea Alto dos Moinhos Metropolitane del mondo Modifica dati su Wikidata · ManualeCoordinate: 38°44′57.98″N 9°10′45.98″W / 38.74944°N 9.17944°W38.74944; -9.17944 Alt...

Sulawesi BaratNama lengkapTim sepak bola Provinsi Sulawesi BaratStadionStadion ManakarraLigaPONPra PON 2024Peringkat 1 di Grup C Kostum kandang Kostum tandang Kostum ketiga Tim sepak bola Provinsi Sulawesi Barat atau Tim sepak bola Sulawesi Barat adalah tim provinsial yang mewakili Sulawesi Barat dalam cabang olahraga sepak bola pada Pekan Olahraga Nasional. Tim ini dikendalikan oleh Asosiasi Provinsi Persatuan Sepak bola Seluruh Indonesia Sulawesi Barat (Asprov PSSI Sulawesi Barat), yang mer...

RRP9 التراكيب المتوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 4J0W, 4JXM المعرفات الأسماء المستعارة RRP9, RNU3IP2, U3-55K, ribosomal RNA processing 9, small subunit (SSU) processome component, homolog (yeast), ribosomal RNA processing 9, U3 small nucleolar RNA binding protein معرفات خارجية MGI: MGI:2384313 HomoloGene: 3452 GeneCards: 9136 علم ا...

Linux standard for directory structure Filesystem Hierarchy StandardAbbreviationFHSStatusPublishedYear started14 February 1994; 30 years ago (1994-02-14)Latest version3.03 June 2015; 8 years ago (2015-06-03)OrganizationLinux FoundationDomainDirectory structureWebsiteOfficial websiteOfficial website (Historical) The Filesystem Hierarchy Standard (FHS) is a reference describing the conventions used for the layout of Unix-like systems. It has been made popular...

كأس تونس للكرة الطائرة للرجال الموسم 1973-1974 البلد تونس المنظم الجامعة التونسية للكرة الطائرة النسخة 18 الفائز النادي الأولمبي القليبي كأس تونس للكرة الطائرة للرجال 1972-1973 كأس تونس للكرة الطائرة للرجال 1974-1975 تعديل مصدري - تعديل كأس تونس للكرة الطائرة للرجال 1973-1974 هو...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Eye injuries and their treatment (1907) The grave of Edward Maitland Ramsay, St Andrews Cemetery Andrew Maitland Ramsay FRSE LLD (1859–1946) was a Scottish eye surgeon and medical author. He was President of the Ophthalmological Society of Great Britain 1923/24 and President of the Royal Medico-Chirurgical Society of Glasgow. Life He was born on 9 November 1859 in Glasgow the son of Andrew Ramsay, a clothier of 66 South Portland Street on the south side of the River Clyde.[1] The f...

Integrated circuits manufacturer Signetics CorporationLogo used from 1971 to 1981IndustryIntegrated circuitsFounded1961FounderDavid Allison, David James, Lionel Kattner, and Mark WeissensternFateAcquired by PhilipsHeadquartersSunnyvale, California, USA Signetics Corporation was an American electronics manufacturer specifically established to make integrated circuits.[1] Founded in 1961, they went on to develop a number of early microprocessors and support chips, as well as the widely ...

Эту страницу предлагается переименовать в «Патриотическая песня (Глинка)».Пояснение причин и обсуждение — на странице Википедия:К переименованию/21 декабря 2022. Пожалуйста, основывайте свои аргументы на правилах именования статей. Не удаляйте шаблон до подведения ито�...

Pour les articles homonymes, voir Gmelin. Christian GmelinChristian GmelinBiographieNaissance 12 octobre 1792TübingenDécès 13 mai 1860 (à 67 ans)TübingenNom dans la langue maternelle Christian Gottlob GmelinNationalité wurtembergeoiseFormation Université Eberhard Karl de Tübingen (à partir du 27 août 1806)Activités Chimiste, professeur d'universitéPère Christian Gottlieb Gmelin (d)Fratrie Ferdinand Gottlieb von Gmelin (en)Autres informationsA travaillé pour Université Ebe...

Questa voce o sezione tratta di una competizione calcistica in corso. Le informazioni possono pertanto cambiare rapidamente con il progredire degli eventi. Se vuoi scrivere un articolo giornalistico sull'argomento, puoi farlo su Wikinotizie. Non aggiungere speculazioni alla voce. Voce principale: Associazione Calcio Monza. AC MonzaStagione 2024-2025Sport calcio Squadra Monza Allenatore Alessandro Nesta All. in seconda Lorenzo Rubinacci Presidente Paolo Berlusconi (onorario) Serie A5º (...

New York Naval MilitiaNew York Naval Militia InsigniaActive1891–presentCountry United States of AmericaAllegiance State of New YorkTypeNaval militiaSize2,800 (approximately)Part ofNew York State Division of Military and Naval AffairsWebsitedmna.ny.gov/nynm/CommandersGovernor of New YorkKathy HochulCommanderRear Admiral Michael Perry[1]Deputy CommanderCaptain David H. HawleyMilitary unit The New York Naval Militia is the naval militia of the state of New York, and is u...

この項目では、2013年時点で現存する大韓民国のテレビ局について説明しています。 「TBC」を略称としていた前身の放送局については「東洋放送」をご覧ください。 2013年時点で「TBC」の略称を用いる大韓民国のテレビ局については「大邱放送」をご覧ください。 JTBC株式会社제이티비씨 주식회사JTBC Co., Ltd. JTBC社屋種類 株式会社本社所在地 韓国ソウル特別市麻浦区上岩...

この項目では、アイルランドで使用されるゲール語について説明しています。英語の方言であり、現代アイルランド人のほとんどが母語としている言語については「アイルランド英語」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2020) مجزرة بيت ريما المعلومات البلد الأراضي الفلسطينية الموقع بيت ريما، محافظة رام الله والبيرة التاريخ 24 أكتوبر 2001 الهدف أعضاء الفدائيون الفلسطينيونوالمق�...

Boxing competitions Men's 57 kg at the 1962 Asian GamesVenueSenayan Tennis StadiumDate27–31 August 1962Competitors8 from 8 nationsMedalists Samphan Payonrathana Thailand Mamoru Hayashi Japan Egino Grafia Philippines Than Tun Burma← 19581966 → Boxing at the1962 Asian Games51 kg67 kg54 kg71 kg57 kg75 kg60 kg81 kg63.5 kg+81 kgvte Main article: Boxing at the 1962 Asian Games The men's ...

У этого термина существуют и другие значения, см. Смоленск (значения). Не следует путать со Смоленском-Сортировочным — другой станцией, также расположенной в Смоленске. СтанцияСмоленск-ЦентральныйМосква-Смоленская — Брест-ЦентральныйВитебск — Смоленск-Центральный�...































































