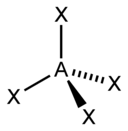
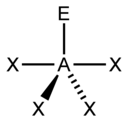
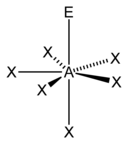
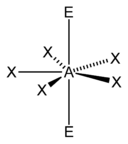
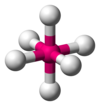
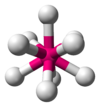
Vegyértékelektronpár-taszítási elmélet
|
Read other articles:

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Mater Dei Institute of Education – news · newspapers · books · scholar · JSTOR (March 2008) (Learn how and when to remove this template message) Mater Dei Institute of EducationInstitiúid Oideachais Mater DeiMottoSapientiam et IntelligentiumTypeRoman CatholicActive1966–2016PresidentMonsignor Dermot Lane...

Iwa GartiwaLahir08 Februari 1966 (umur 58)Bandung, Jawa Barat, IndonesiaPekerjaanPengusaha, PolitisiPartai politikNasDemSuami/istriIsyanuari PrihastriantiAnak5Situs webiwa-gartiwa.ahlinyaweb.com Ir. Iwa Gartiwa, M.M. (lahir 08 Februari 1966) adalah seorang pengusaha kelahiran Bandung berkebangsaan Indonesia. Ia menjabat sebagai Ketua Kamar Dagang dan Industri (KADIN) Kota Bandung dua periode 2016–2021 dan 2021–2026, ia juga aktif dan memegang suatu jabatan di berbagai organisasi lai...

.skJenis TLDTLD kode negara InternetStatusAktifRegistriSK-NICSponsorSK-NICPemakaian yang diinginkanEntitas yang terhubung dengan SlovakiaPemakaian aktualDigunakan di SlovakiaDomain terdaftar380.408 (2018-08-24)[1]PembatasanTak adaStrukturRegistrasi dilakukan secara langsung di tingkat kedua dan ketigaSitus webSK-NIC .sk adalah top-level domain kode negara Internet untuk Slowakia. lbsRanah tingkat teratas kode negara (ccTLD)ISO 3166-1 A .ac .ad .ae .af .ag .ai .al .am .ao .a...

Pour les articles homonymes, voir Wi-Fi (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (mars 2023). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Exemple d'application du Wi-Fi : impress...

Cet article est une ébauche concernant le Concours Eurovision de la chanson et l’Allemagne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) ; pour plus d’indications, visitez le projet Eurovision. Allemagneau Concours Eurovision 1979 Données clés Pays Allemagne Chanson Dschinghis Khan Interprète Dschinghis Khan Langue Allemand Sélection nationale Radiodiffuseur BR Type de sélection Finale nationaleÉmission télévisée : Ein Lied für Jer...

Wali Kota Padang PanjangPetahanaSonny Budaya PutraPenjabatsejak 12 Oktober 2023KediamanRumah Dinas Wali Kota Padang PanjangMasa jabatan5 tahunDibentuk1957Pejabat pertamaUmar AliSitus webwww.padangpanjang.go.id Wali Kota Padang Panjang adalah politisi yang dipilih untuk bertanggung jawab dalam mengatur dan mengelola Pemerintah Kota Padang Panjang, sebagai bagian dari sistem penyelenggaraan pemerintahan daerah di Indonesia. Daftar Wali Kota Berikut adalah Daftar Wali Kota Padang Panjang se...

Museo Diffuso della Resistenza, della Deportazione, della Guerra, dei Diritti e della Libertà UbicazioneStato Italia LocalitàTorino IndirizzoPalazzo dei Quartieri Militari (Polo del '900) Corso Valdocco, 4/A Coordinate45°04′33.04″N 7°40′26.59″E / 45.075844°N 7.674053°E45.075844; 7.674053Coordinate: 45°04′33.04″N 7°40′26.59″E / 45.075844°N 7.674053°E45.075844; 7.674053 CaratteristicheTipoResistenza, guerra, storia Aperturamaggio 20...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

This article is about the Beatles song. For other uses, see Cry Baby Cry (disambiguation). 1968 song by the BeatlesCry Baby CryCover of the Northern Songs sheet musicSong by the Beatlesfrom the album The Beatles Released22 November 1968Recorded15, 16, 18 July 1968StudioEMI, LondonGenreRockLength3:03LabelAppleSongwriter(s)Lennon–McCartneyProducer(s)George Martin Cry Baby Cry is a song by the English rock band the Beatles from their 1968 double album The Beatles (also known as the White Album...

1962 dark fantasy novel by Ray Bradbury Something Wicked This Way Comes First edition dust jacket art by Gray FoyAuthorRay BradburyCountryUnited StatesLanguageEnglishGenreFantasyHorrorSupernaturalPublisherSimon & SchusterPublication dateSeptember 17, 1962[1]Media typePrint (hardcover and paperback)Pages293ISBN0-671-67960-0 (first edition); See release details for othersOCLC9194864Preceded byDandelion Wine Followed byThe Halloween Tree Something Wicked Thi...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Cemal PashaLahir(1872-05-06)6 Mei 1872Midilli, Kesultanan UtsmaniyahMeninggal21 Juli 1922(1922-07-21) (umur 50)Tbilisi, Republik Sosialis Soviet GeorgiaPengabdian Kesultanan UtsmaniyahLama dinas1893–1918PangkatJenderalKesatuanMenteri Angkatan LautKomandanAngkatan Darat KeempatPerang/pertempuranPeperangan Balkan, kampanye militer Sinai dan Palestina, kampanye militer Mesopotamia (1915-1917) Ahmed Djemal Pasha (Turki Otoman: احمد جمال پاشا, modern Turki: Ahm...

Thubten Gyatso, the 13th Dalai Lama photographed in Calcutta in 1910 There were three main feudal social groups in Tibet prior to 1959, namely ordinary laypeople (mi ser in Tibetan), lay nobility (sger pa), and monks.[1] The ordinary layperson could be further classified as a peasant farmer (shing-pa)[citation needed] or nomadic pastoralist (trokpa).[citation needed] To influence politics and religious domination, entering into monkhood and military was required. (Suna...

Magnetic phenomenon Fig. 1.—Arago's spinning diskFig. 2.—Babagge and Herschel's experimentFig. 3.—Slit disks used by Babbage and HerschelArago's rotations is an observable magnetic phenomenon that involves the interactions between a magnetized needle and a moving metal disk. The effect was discovered by François Arago in 1824. At the time of their discovery, Arago's rotations were surprising effects that were difficult to explain. In 1831, Michael Faraday introduced the theory of elect...

Lynching of Jim McIlherronLocationEstill Springs, Tennessee, U.S.DateFebruary 12, 1918Attack typeLynching Part of a series on theNadir of Americanrace relationsViolence in the 1906 Atlanta race massacre Historical background Reconstruction era Voter suppression Disfranchisement Redeemers Compromise of 1877 Jim Crow laws Segregation Anti-miscegenation laws Convict leasing Practices Common actions Expulsions of African Americans Lynchings Lynching postcards Sundown town Whitecapping Vigilante g...

Russian-Australian boxer (born 1969) In this name that follows Eastern Slavic naming customs, the patronymic is Borisovich and the family name is Tszyu. Kostya TszyuКостя ЦзюTszyu in 2008BornKonstantin Borisovich Tszyu (1969-09-19) 19 September 1969 (age 54)Serov, Russian SFSR,Soviet UnionNationality Australian (since 1993) Soviet (until 1991) Other namesThunder from Down UnderStatisticsWeight(s)Light-welterweightHeight5 ft 7 in (170 cm)[1]Reach67&...

Tembok Romawi Eboracum adalah benteng dan kota di Britania Romawi. Eboracum berada di lokasi yang saat ini merupakan bagian dari kota York, Yorkshire Utara, Inggris. Sebagai pelabuhan yang sibuk dan ibu kota provinsi, Eboracum adalah kota multikultural dengan penduduk yang berasal dari seluruh Kekaisaran Romawi.[1] Eboracum merupakan basis militer utama di Britania Utara. Saat pembagian provinsi Britannia, Eboracum menjadi ibu kota provinsi Britannia Inferior. Lalu pada tahun 296, Bri...

1857 conflict between police forces in front of New York City Hall, NY, USA Not to be confused with the 1992 Patrolmen's Benevolent Association Riot. New York City Police riot of 1857Part of the History of the New York City Police Department and History of New York City (1855–1897)New York City Municipal and Metropolitan policemen riot and fight each other in front of New York City Hall in 1857DateJune 16, 1857LocationNew York City, New York, United StatesResult Riot crushedCasualties and l...

Massacro di piazza Rabi'a al-'AdawiyyaUna ruspa dell'esercito rimuove le barricate Data14 agosto 2013 LuogoPiazza Rabi'a al-'Adawiyya, Il Cairo Stato Egitto ObiettivoSostenitori di Mohamed Morsi e del Partito Libertà e Giustizia ResponsabiliForze di sicurezza egiziane ConseguenzeMorti817 (secondo Human Rights Watch)638 (secondo il ministero della Salute egiziano)2.600 (secondo i Fratelli Musulmani) Feritialmeno 3994 Modifica dati su Wikidata · Manuale Il massacro di piazza Rabi'a ...
Archidiocèse de Santiago du Chili Informations générales Pays Chili Archevêque Fernando Chomalí Langue(s) liturgique(s) espagnol Superficie 9 193 km2 Création du diocèse 27 juin 1561 Élévation au rang d'archidiocèse 21 mai 1840 Diocèses suffragants LinaresMelipillaRancaguaSan BernardoSan FelipeTalcaValparaíso Site web site officiel Statistiques Population 6 104 413 hab. (2020) Population catholique 4 162 700 fidèles (2020) Pourcentage de c...