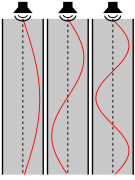
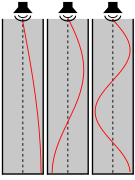
גל עומד
| |||||||||||||||
Read other articles:

1967 song by Aretha Franklin (You Make Me Feel Like) A Natural WomanSide A of the US singleSingle by Aretha Franklinfrom the album Lady Soul B-sideBaby, Baby, BabyReleasedSeptember 1967Recorded1967StudioAmerican Sound Studio, Memphis, TennesseeGenreSoulLength2:45LabelAtlanticSongwriter(s)Gerry GoffinCarole KingJerry WexlerProducer(s)Jerry WexlerAretha Franklin singles chronology Baby I Love You (1967) (You Make Me Feel Like) A Natural Woman (1967) Chain of Fools (1967) Lyric video(You Make Me...

Acetobacter SEM dari Acetobacter aceti Klasifikasi ilmiah Domain: Bacteria Filum: Proteobacteria Kelas: Alphaproteobacteria Ordo: Rhodospirillales Famili: Acetobacteraceae Genus: AcetobacterBeijerinck 1898 Spesies tipe Acetobacter aceti Spesies A. aceti A. cerevisiae A. cibinongensis A. estunensis A. indonesiensis A. liquefaciens A. lovaniensis A. malorum A. nitrogenifigens A. oeni A. orientalis A. orleanensis A. pasteurianus A. peroxydans A. pomorum A. syzygii A. tropicalis Acetobacter adal...

Sondershausen Lambang kebesaranLetak Sondershausen di Kyffhäuserkreis NegaraJermanNegara bagianThüringenKreisKyffhäuserkreisSubdivisions12Pemerintahan • MayorJoachim Kreyer (CDU)Luas • Total114,36 km2 (4,415 sq mi)Ketinggian208 m (682 ft)Populasi (2013-12-31)[1] • Total21.907 • Kepadatan1,9/km2 (5,0/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos99701–99706Kode area telepon03632Pelat kendaraanKYF, ART...

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis. dr. H.Mundjirin ESSp.OG Bupati Semarang ke-39Masa jabatan17 Februari 2016[1] – 17 Februari 2021GubernurGanjar PranowoWakilNgesti Nugraha PendahuluSujarwanto Dwiatmoko (Pj.)PenggantiNgesti NugrahaMasa jabatan2010 – 2015GubernurBibit WaluyoGanjar PranowoWakilWarnadi PendahuluSiti Ambar FathonahPenggantiSujarwanto Dwiat...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Messiah novel – news · newspapers · books · scholar · JSTOR (November 2016) (Learn how and when to remove this template message) The Messiah AuthorMarjorie HolmesCountryUnited States and CanadaLanguageEnglishGenreChristian novelsPublisherHarper & R...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (décembre 2008). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) الدوري التركي الممتازالموسم2009–10البطلبورصا سبورهابطونعثمانلي سبوردنيزلي سبوردياربكر سبوردوري أبطال أ...

Fashion school of the State University of New York Fashion Institute of TechnologyTypePublic collegeEstablished1944; 80 years ago (1944)Parent institutionState University of New YorkPresidentJoyce F. BrownStudents8,767[1]Undergraduates8,555Postgraduates212LocationNew York City, United States40°44′48″N 73°59′39″W / 40.74667°N 73.99417°W / 40.74667; -73.99417CampusUrban, 1.5 blocksNicknameTigersMascotStitchWebsitewww.fitnyc.edu The F...

Italian Volleyball FederationSport Volleyball Beach volleyballJurisdictionItalyAbbreviationFIPAVFounded1946 (1946)AffiliationFIVBAffiliation date1947 (1947)HeadquartersRomeLocationItalyPresidentGiuseppe ManfrediOfficial websitewww.federvolley.it The Italian Volleyball Federation (Italian: Federazione Italiana Pallavolo, FIPAV) is the governing body for volleyball in Italy since 1946.[1] The FIPAV has reported a significant increase in its membership numbers, with over 300,00...

2004 single by Alicia Keys KarmaSingle by Alicia Keysfrom the album The Diary of Alicia Keys ReleasedNovember 1, 2004 (2004-11-01)Studio KrucialKeys Quad Recording (New York City, New York) Genre R&B alternative hip hop classical Length4:16LabelJSongwriter(s) Alicia Keys Kerry Brothers, Jr. Taneisha Smith Producer(s)Brothers, Jr.Alicia Keys singles chronology My Boo (2004) Karma (2004) Unbreakable (2005) Music videoKarma on YouTube Karma is a song by American singer and so...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Gangguan somatoform merupakan gangguan kecemasan atau ketegangan psikologi yang berupa keluhan dibagian fisik tetapi secara medis gejala-gejala fisik yang dialami tidak terbukti kebenarannya. Gangguan ini sering juga disebut dengan briquet's syndrom. G...

Daftar ini, merupakan daftar para pemimpin Jerman Timur: Sekretaris Jendral Partai Persatuan Sosialis Jerman Bahasa Jerman: Erster Sekretär des Zentralkomitees der Sozialistische Einheitspartei Deutschlands, Generalsekretärs des ZK der SED. Logo of the Socialist Unity Party of Germany No Foto Nama(lahir-mati) Jabatan dimulai Jabatan berakhir Partai politik Ketua Bersama Partai Persatuan Sosialis JermanVorsitzende der Sozialistischen Einheitspartei Deutschlands Wilhelm Pieck(1876–1960) 22 ...

British linguist (1920–2017) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (December 2017) (Learn how and when to remove this message) The Right HonourableThe Lord QuirkCBE FBALord Quirk in 2016Member of the House of LordsLord TemporalIn office12 July 1994 – 20 December 2017Vice-Chancellor of University of ...

Arvind VirmaniFull time member of NITI AayogIncumbentAssumed office 16th November 202213th Chief Economic Adviser to the Government of IndiaIn office2007 - 2009 Personal detailsBorn (1949-06-22) 22 June 1949 (age 74)NationalityIndianAlma materDelhi University (BSc)Caltech (BS)Harvard University (MA, PhD)ProfessionEconomist Arvind Virmani (born 22 June 1949) is an Indian economist and full time Member of NITI Aayog. He was appointed India's representative to the International Monetar...

President of Planned Parenthood (2008-2018) Cecile RichardsPresident of Planned ParenthoodIn officeFebruary 2006 – April 2018Preceded byGloria FeldtSucceeded byLeana Wen Personal detailsBorn (1957-07-15) July 15, 1957 (age 66)Waco, Texas, U.S.SpouseKirk AdamsChildren3ParentAnn Richards (mother)ResidenceNew York CityEducationBrown University (BA) Cecile Richards (born July 15, 1957)[1] is an American activist who served as the president of the Planned Parenthood Federat...

236-я гвардейская артиллерийская бригада Годы существования 1 декабря 2017[1] — н. в. Страна Россия Подчинение Сухопутные войска Входит в 20-я гвардейская общевойсковая армия Тип артиллерийская бригада Функция ствольная артиллерияреактивная артиллерия Часть Моск...

Militant organization in control of Afghanistan For other uses, see Taliban (disambiguation). This article is about the Afghan group. Not to be confused with Pakistani Taliban, Jamaat Ansarullah, or Punjabi Taliban. This article may be too long to read and navigate comfortably. When this tag was added, its readable prose size was 17,000 words. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (June 2022) T...

تمارة تمارة[1](بالفرنسية: Témara)[1] تاريخ التأسيس القرن 12 تقسيم إداري البلد المملكة المغربية[2] عاصمة لـ عمالة الصخيرات تمارة الولاية الرباط سلا القنيطرة الإقليم عمالة الصخيرات - تمارة المسؤولون رئيس الجماعة زهير الزمزامي[3][4] خصائص جغرافية إح�...

2019 single by David Guetta, Brooks & LooteBetter When You're GoneSingle by David Guetta, Brooks & LooteReleased8 February 2019Recorded2018GenreFuture bounceLength3:12LabelWhat a MusicSongwriter(s)David GuettaIdo ZmishlanyThijs WestbroekJackson FooteEmma Lov BlockJeremy DussollietProducer(s)BrooksDavid Guetta singles chronology Say My Name (2018) Better When You're Gone (2019) Ring the Alarm (2019) Brooks singles chronology Limbo(2018) Better When You're Gone(2019) Waiting for Lov...

Battle of the First Carlist War Battle of AlsasuaPart of the First Carlist WarDate22 April 1834LocationAlsasua (Altsasu), Navarre, Spain42°53′43″N 2°10′08″W / 42.8953°N 2.1689°W / 42.8953; -2.1689Result Carlist victoryBelligerents Carlists supporting Infante Carlos of Spain Liberals (Isabelinos or Cristinos) supportingIsabella II of Spain and her regent mother Maria ChristinaCommanders and leaders Tomás de Zumalacárregui Vicente Genaro de QuesadaCasualtie...