נוסחת האנטרופיה של בולצמן
|
Read other articles:

American politician Milton Andrew RomjueRomjue circa 1917Member of theU.S. House of Representativesfrom MissouriIn officeMarch 4, 1917 – March 3, 1921Preceded byJames Tilghman LloydSucceeded byFrank C. MillspaughConstituency1st districtIn officeMarch 4, 1923 – January 3, 1943Preceded byFrank C. MillspaughSucceeded bySamuel W. ArnoldConstituency1st district (1923–33)At-large (1933–35)1st district (1935–43) Personal detailsBorn(1874-12-05)December 5, 1874Macon County...

Ini adalah nama Korea; marganya adalah Yoon. Yoon Si-yoonYoon pada Agustus 2020Nama asal윤시윤LahirYoon Dong-gu26 September 1986 (umur 37)Suncheon, Provinsi Jeolla Selatan, Korea SelatanKebangsaanKorea SelatanPekerjaanAktor, entertainer, presenter televisiTahun aktif2009-sekarangNama KoreaHangul윤시윤 Hanja尹施允 Alih AksaraYun Si-yunMcCune–ReischauerYun SiyunNama lahirHangul윤동구 Hanja尹東久 Alih AksaraYun Dong-guMcCune–ReischauerYun Tonggu Yoon Si-yoon (Ha...

American politician Anna TovarMember of the Arizona Corporation CommissionIncumbentAssumed office January 11, 2021Preceded byBob BurnsMember of the Arizona Senatefrom the 19th districtIn officeJanuary 14, 2013 – January 5, 2015Preceded byRich CrandallSucceeded byLupe ContrerasMember of the Arizona House of Representativesfrom the 13th districtIn officeJanuary 2009 – January 14, 2013Preceded bySteve GallardoSucceeded byDarin Mitchell Personal detailsPoliti...

Ganes THGanes THLahirThio Thiauw San(1935-07-10)10 Juli 1935 Tangerang, Jawa Barat, Hindia BelandaMeninggal10 Desember 1995(1995-12-10) (umur 60)PekerjaanKomikusKebangsaanIndonesiaGenreKomik, Cerita silat Ganes Thiar Santosa (Thio Thiauw San) (10 Juli 1935 – 10 Desember 1995), atau lebih dikenal dengan nama pena singkatnya Ganes TH. adalah seorang komikus Indonesia terkenal. Ia merupakan salah satu tonggak kejayaan komik Indonesia. Pada masanya Ganes TH. merupakan salah s...

Boatbuilder in Maldon, Essex, England Barge blocks in the River Blackwater at Cooks Yard Cooks Yard is a boat-building business established by Walter Cook in 1894 on the bank of the River Blackwater at Maldon, Essex, England. Originally known as Walter Cook and Son and specialising in the building of Thames sailing barges, it operated until the 1980s - at which time, it was the last remaining barge yard in Britain. In 1999, Topsail Charters took on the lease of the yard and refurbished it. Th...

1875 Pennsylvania gubernatorial election ← 1872 November 2, 1875 (1875-11-02) 1878 → Nominee John F. Hartranft Cyrus L. Pershing Party Republican Democratic Popular vote 304,175 292,145 Percentage 49.9% 47.9% County results Hartranft: 40–50% 50–60% 60–70% Pershing: 40–50% 50–60% &...

Mountain pass across the Julian Alps in Slovenia This article is about the Slovenian pass. For the Slovenian footballer, see Dare Vršič. Vršič PassThe Vršič PassElevation1,611 m (5,285 ft)Traversed byRuska cestaLocationUpper Carniola, SloveniaRangeJulian AlpsCoordinates46°26′8″N 13°44′40″E / 46.43556°N 13.74444°E / 46.43556; 13.74444Vršič PassLocation of the Vršič Pass The Vršič Pass (pronounced [ʋəɾˈʃitʃ]; Slovene: prelaz Vršič,...
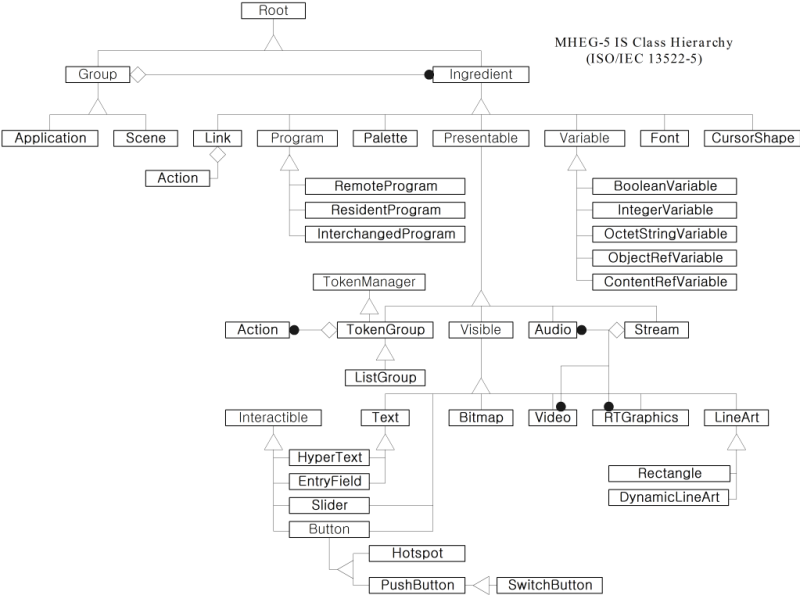
Set of international standards Not to be confused with MPEG. MHEG-5, or ISO/IEC 13522–5,[1] is part of a set of international standards relating to the presentation of multimedia information, standardised by the Multimedia and Hypermedia Experts Group (MHEG). It is most commonly used as a language to describe interactive television services. Characteristics MHEG-5 is a licence-free and public standard for interactive TV middleware that is used both to send and receive interactive TV...

American politician Loren E. WheelerMember of the U.S. House of Representativesfrom Illinois's 21st districtIn officeMarch 4, 1925 – March 3, 1927Preceded byJames Earl MajorSucceeded byJames Earl MajorIn officeMarch 4, 1915 – March 3, 1923Preceded byJames McMahon GrahamSucceeded byJames Earl Major Personal detailsBorn(1862-10-07)October 7, 1862Havana, IllinoisDiedJanuary 8, 1932(1932-01-08) (aged 69)Springfield, IllinoisPolitical partyRepublican Loren Ed...

Oj, svijetla majska zoroB. Indonesia: Oh, Cahaya Fajar Bulan MeiОј, свијетла мајска зороLagu kebangsaan MontenegroPenulis lirikSekula DrljevićKomponisŽarko MirkovićPenggunaan2004 (resmi)Sampel audioOj, svijetla majska zoroberkasbantuan Sampel audioOj, svijetla majska zoroberkasbantuan Oj, svijetla majska zoro adalah lagu kebangsaan Montenegro. Lirik Aksara Latin (Resmi) Oj svijetla majska zoro, Majko naša Crna Goro, Sinovi smo tvog stijenja I čuvari tvog po...

Finnish politician Juho Koivisto in 1941 Juho Koivisto's gravestone in Kurikka cemetery, Finland Johannes (Juho) Koivisto (15 March 1885, in Kurikka – 13 October 1975; original surname Keski-Koivisto) was a Finnish farmer and politician. He served as Deputy Minister of Agriculture from 4 July 1930 to 21 March 1931 and from 12 March 1937 to 4 January 1941 and as Deputy Minister of Finance from 4 January 1941 to 5 March 1943. He was a member of the Parliament of Finland from 1927 to 1951, re...

Lokasi Pelagonia Pelagonia dilihat dari Gunung Baba Pelagonia (Yunani: Πελαγονíα, Pelagonía; Makedonia: Пелагонија, Pelagonija) adalah sebuah kawasan geografi Makedonia yang diambil dari nama kerajaan kuno. Pelagonia Kuno meliputi munisipalitas-munisipalitas modern Prilep, Mogila, Novica, Krushevo, dan Krivogashtani di Makedonia Utara. Referensi Pranala luar Pelagonian margins in central Evia island (Greece) Diarsipkan 2005-11-01 di Wayback Machine. The oldest rocks of Gre...

French botanist and mycologist (1843–1901) Maxime Cornue Marie Maxime Cornu (July 16, 1843, in Orléans – April 3, 1901 in Paris) was a French botanist and mycologist.[1] He was a younger brother of physicist Alfred Cornu (1841-1902). He studied at the École normale supérieure, and in 1872 received his doctorate in natural sciences. He served as aide-naturaliste at Museum National d'Histoire Naturelle in Paris, where from 1876 he worked as a lecturer of botany.[2] From 1...

† Большая гавайская древесница Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:За...

«Napoleón» redirige aquí. Para otras acepciones, véase Napoleón (desambiguación). Napoleón Bonaparte Emperador de los francesesCopríncipe de AndorraRey de ItaliaProtector de la Confederación del Rin Retrato de Napoleón en su gabinete de trabajo, en el palacio de las Tullerías. Jacques-Louis David, 1812.Emperador de los franceses 18 de mayo de 1804-3[1]/11 de abril de 1814[2]Predecesor Charles-François Lebrun(como tercer cónsul)Sucesor Luis XVIII(como rey de Francia...

Genus of birds Myiarchus Brown-crested flycatcherMyiarchus tyrannulus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Passeriformes Family: Tyrannidae Genus: MyiarchusCabanis, 1844 Type species Muscicapa feroxGmelin, JF, 1789 Myiarchus is a genus of birds in the tyrant flycatcher family Tyrannidae. Most species are fairly similar in appearance and are easier to separate by voice than by plumage. Myiarchus flycatchers are fairly large tyrant-fl...

Type of telescope Not to be confused with Celestial cartography. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Astrograph – news · newspapers · books · scholar · JSTOR (May 2014) (Learn how and when to remove this message) A 13-inch (330 mm), f/5.3 astrograph at Lowell Observatory (a refractor with a ...

Professional basketball team in Shibuya, Tokyo, Japan Sun Rockers ShibuyaLeaguesB.LeagueFounded1935; 89 years ago (1935)HistoryHitachi Honsha Rising Sun1935–2000Hitachi SunRockers2001–2013Hitachi SunRockers Tokyo-Shibuya2016–2017ArenaAoyama Gakuin University Memorial HallCapacity2,500LocationShibuya, TokyoHead coachKen HamanakaRetired numbers2 (11, 20)WebsiteOfficial site Home Away Sun Rockers Shibuya is a Japanese professional basketball team based in Tokyo and acquir...

Cet article est une ébauche concernant une localité pakistanaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Karor Lal Esanكروڑ لعل عيسن Sanctuaire de Lal Esan Administration Pays Pakistan Province Pendjab Division Dera Ghazi Khan District Layyah Démographie Population 35 267 hab. (rec. 2017) Géographie Coordonnées 31° 13′ nord, 70° 57′ est Localisation G�...

Clade of reptiles MesochelydiaTemporal range: Early Jurassic–Present PreꞒ Ꞓ O S D C P T J K Pg N Kayentachelys Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Clade: Pantestudines Clade: Testudinata Clade: Rhaptochelydia Clade: MesochelydiaJoyce, 2017 Subgroupings †Condorchelys †Eileanchelys †Heckerochelys †Indochelys †Kayentachelys Perichelydia Mesochelydia (from Greek mesos middle and chelys turtle) is a clade within Pantestudin...
















![{\displaystyle P(k)\propto {\frac {N^{k}}{2^{N}}}\ \ {\xrightarrow[{N\rightarrow \infty }]{}}\ \ 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dfc2e2653befad574907a022ece2868f4e5f529)

































