![]() ОаОЎОфОЪ ОюОцОеОЋОЕ ОўОАОеОДОў ОюОЕОъОЋОаОћ ОДОЋОЉОЎОЋОф ОфОюОфоЙОъОъОЊОЎОЋОф ОЏОЕОЮ ОЕОаОЎОфОЪ ОюОцОеОЋОА ОДОЋОЉОЎОЎОћ ОюОЕОЎОЕОћ ОеОЎОЉОЋОбОЎОЮ ОЊОЋоЙОъОъОЊОЎОЎОЮ
ОаОЎОфОЪ ОюОцОеОЋОЕ ОўОАОеОДОў ОюОЕОъОЋОаОћ ОДОЋОЉОЎОЋОф ОфОюОфоЙОъОъОЊОЎОЋОф ОЏОЕОЮ ОЕОаОЎОфОЪ ОюОцОеОЋОА ОДОЋОЉОЎОЎОћ ОюОЕОЎОЕОћ ОеОЎОЉОЋОбОЎОЮ ОЊОЋоЙОъОъОЊОЎОЎОЮ
ОўохОАохОеоиОДо░Оў ОћОЋОљ ОњОЋОБ ОЉОъОеОЌОЉ ОљОеОЉОб-ОъОъОЊОЎ ОћОъОћОЋОЋОћ ОћОЎОцОеОДОЋОЉОЎОћ ОъОъОъОЊ 4.
ОћОўОАОеОДОў ОћОЋОљ ОћОЏОюОюОћ ОЕОю ОћОДОЋОЉОЎОЎОћ ОћОъОЋОЏОеОф ОЉОњОљОЋОъОўОеОЎОћ ОЕОю ОћОъОеОЌОЉ ОћОфОюОф-ОъОъОЊОЎ.
ОћОЎОЌОА ОЉОЎОЪ ОћОўОАОеОДОў ОюОДОЋОЉОЎОЎОћ ОЊОЋОъОћ ОюОќОћ ОЕОЉОЎОЪ ОћОДОЋОЉОЎОЎОћ ОюОеОЎОЉОЋОб. ОЏОЕОЮ ОЕОДОЋОЉОЎОЎОћ ОћОЎОљ ОњОЋОБ ОфОюОф-ОъОъОЊОЎ ОЕОюОЋ ОЕОЕ ОцОљОЋОф ОеОЎОЉОЋОбОЎОЋОф, ОћОўОАОеОДОў ОћОЋОљ ОњОЋОБ ОљОеОЉОб-ОъОъОЊОЎ ОЉОбОю ОЕОъОЋОаОћ "ОцОљОЋОф" ОфОюОф-ОъОъОЊОЎОЋОф ОДОЋОЉОЎОЎОфОЎОЋОф. ОўОАОеОДОў ОћОЋОљ ОљОЌОЊ ОъОЕОЕОф ОћОцОљОЋОаОЎОЮ ОћОљОеОЉОб-ОъОъОЊОЎОЎОЮ ОћОДОъОЋОеОЎОЮ ОћОъОЕОЋОЏОюОюОЎОЮ.
ОљОф ОћОъОЋОаОЌ "ОўОАОеОДОў" ОўОЉОб ОЉОЕОаОф 1888 ОћОъОфОъОўОЎОДОљОЎ ОћОЉОеОЎОўОЎ Од'ОљОеОюОА ОћОљОЋОЋОеОЊ ОћОЎОаОўОЋОЪ, ОЋОъОДОЋОеОЋ ОЉОъОЎОюОЎОЮ ОћОЎОЋОЋОаОЎОЋОф "ОўОАОеОћ" (¤ё╬Г¤Ѓ¤Ѓ╬▒¤Ђ╬▒, "ОљОеОЉОб") ОЋ"ОљОДОўОЎОА" (р╝ђ╬║¤ё╬»¤ѓ, "ОДОеОЪ"), ОћОъОфОЎОЎОЌОАОЋОф ОюОљОеОЉОбОф ОћОъОДОдОЋОбОЋОф (ОћОЌОЊоЙОъОъОЊОЎОЎОЮ) ОћОъОЌОЉОеОЎОЮ ОљОф ОЏОю ОљОЌОЊ ОъОДОЋОЊОДОЋОЊОЎ ОћОўОАОеОДОў ОюОЕОЏОаОЎОЋ.
ОфОЏОЋОаОЋОф ОћОўОАОеОДОў
ОюОўОАОеОДОў ОЎОЕ 16 ОДОЋОЊОДОЋОЊОЎОЮ, 32 ОъОДОдОЋОбОЋОф, 24 ОцОљОЋОф ОЊОЋ-ОъОъОЊОЎОЋОф, ОЋ-8 ОцОљОЋОф ОфОюОф-ОъОъОЊОЎОЋОф ("ОфОљОЎОЮ"). ОЉОЏОю ОДОЋОЊОДОЋОЊ ОЕОю ОћОўОАОеОДОў ОаОцОњОЕОЎОЮ 4 ОъОДОдОЋОбОЋОф, 6 ОцОЎОљОЋОф ОЊОЋоЙОъОъОЊОЎОЋОф, ОЋ-4 ОфОљОЎОЮ ОфОюОф-ОъОъОЊОЎОЎОЮ.
ОћОъОеОЌОД ОЉОЎОЪ ОЏОю ОДОЋОЊОДОЋОЊ ОЕОю ОћОўОАОеОДОў ОюОъОеОЏОќ ОћОўОАОеОДОў РђЊ ОаОДОЋОЊОћ ОЕОъОеОЌОДОћ ОъОЏОю ОДОЋОЊОДОЋОЊОЎ ОћОўОАОеОДОў ОЕОЋОЋОћ РђЊ ОћОЋОљ ОЏОљОЋОеОџ ОћОъОДОдОЋОб ОЕОю ОћОўОАОеОДОў. ОћОъОеОЌОД ОЉОЎОЪ ОЕОаОЎ ОДОЋОЊОДОЋОЊОЎОЮ ОаОњОЊОЎОЎОЮ ОЕОю ОўОАОеОДОў ОћОЋОљ ОЏОцОЋОю ОъОљОЋОеОџ ОћОъОДОдОЋОб ОЕОю ОћОўОАОеОДОў.
ОЉОаОЎОЎОф ОћОўОАОеОДОў
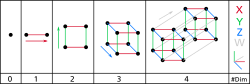 ОфОеОЕОЎОЮ ОюОцОЎОфОЋОЌ ОћОЊОеОњОфОЎ ОЕОю ОеОбОЎОЋОЪ ОћОўОАОеОДОў
ОфОеОЕОЎОЮ ОюОцОЎОфОЋОЌ ОћОЊОеОњОфОЎ ОЕОю ОеОбОЎОЋОЪ ОћОўОАОеОДОў
ОаОЎОфОЪ ОюОЉОаОЋОф ОўОАОеОДОў ОЉОљОЋОцОЪ ОћОЉОљ, ОфОЋОџ ОћОњОЊОюОћ ОћОЊОеОњОфОЎОф ОЕОю ОъОАОцОе ОћОъОъОЊОЎОЮ:
- ОЌОЊ-ОъОъОЊОЎ: ОЌОЎОЉОЋОе ОЕОю ОЕОфОЎ ОаОДОЋОЊОЋОф, A ОЋ-B ОЉОДОЋ ОЎОЕОе ОЎОЋОдОе ОДОўОб AB.
- ОЊОЋ-ОъОъОЊОЎ: ОљОф ОћОДОдОЋОЋОф ОЕОю ОЕОаОЎ ОДОўОбОЎОЮ ОќОћОЎОЮ ОЉОљОЋОеОЏОЮ, AB ОЋ-CD, ОЕОћОъОеОЌОД ОЉОЎОаОЎОћОЮ ОћОЋОљ ОЏОљОЋОеОџ ОЏОю ОљОЌОЊ ОъОћОЮ, ОаОЎОфОЪ ОюОЌОЉОе ОЋОюОЎОдОЋОе ОеОЎОЉОЋОб ABCD. ОюОљ ОаОЎОфОЪ ОюОбОЕОЋОф ОќОљОф ОфОЋОџ ОЕОЎОъОЋОЕ ОЉОъОъОЊ ОљОЌОЊ ОЉОюОЉОЊ, ОљОюОљ ОеОД ОЉОъОЎОЕОЋОе ОЊОЋ-ОъОъОЊОЎ.
- ОфОюОф-ОъОъОЊОЎ: ОљОф ОћОДОЋОЊОДОЋОЊОЎОЮ ОЕОю ОЕОаОЎ ОеОЎОЉОЋОбОЎОЮ ОЌОЋОцОцОЎОЮ ABCD ОЋ-EFGH, ОЕОћОъОеОЌОД ОЉОЎОаОЎОћОЮ ОћОЋОљ ОЏОљОЋОеОџ ОћОдОюОб ОЕОю ОЏОю ОљОЌОЊ ОъОћОЮ, ОаОЎОфОЪ ОюОЌОЉОе ОЋОюОЎОдОЋОе ОДОЋОЉОЎОЎОћ ABCDEFGH. ОюОљ ОаОЎОфОЪ ОюОбОЕОЋОф ОќОљОф ОфОЋОџ ОЕОЎОъОЋОЕ ОЉОЕОаОЎ ОъОъОЊОЎОЮ ОЉОюОЉОЊ, ОљОюОљ ОеОД ОЉОъОеОЌОЉ ОфОюОф-ОъОъОЊОЎ.
- ОљОеОЉОб-ОъОъОЊОЎ: ОљОф ОћОДОЋОЊОДОЋОЊОЎОЮ ОЕОю ОЕОфОЎ ОДОЋОЉОЎОЋОф ОЕОљОЋОеОџ ОъОДОдОЋОбОЪ ОќОћОћ, ABCDEFGH ОЋ-IJKLMNOP, ОЋОћОъОеОЌОД ОЉОЎОаОЎОћОЪ ОћОЋОљ ОЏОљОЋОеОџ ОћОъОДОдОЋОб ОЕОю ОЏОю ОљОЌОф ОъОћОЪ, ОаОЎОфОЪ ОюОЌОЉОе ОЋОюОЎОдОЋОе ОўОАОеОДОў ABCDEFGHIJKLMNOP. ОюОљ ОаОЎОфОЪ ОюОбОЕОЋОф ОќОљОф ОфОЋОџ ОЕОЎОъОЋОЕ ОЉОЕОюОЋОЕОћ ОъОъОЊОЎОЮ ОЉОюОЉОЊ, ОљОюОљ ОеОД ОЉОъОеОЌОЉ ОљОеОЉОб-ОъОъОЊОЎ.
ОћОЎОўОюОЎОЮ ОЕОЋОаОЎОЮ ОЕОю ОћОўОАОеОДОў
-
ОЊОЎОљОњОеОъОф ОЕОюОњОю (ОљОа') ОЕОю ОћОўОАОеОДОў (
ОћОЎОўОю). ОЉОъОЋОаОЌОЎОЮ ОљОЎОаОўОЋОљОЎОўОЎОЉОЎОЎОЮ, ОаОЎОфОЪ ОюОеОљОЋОф ОќОљОф ОЏ"ОъОбОЎОЏОћ" ОЕОю ОўОАОеОДОў ОюОъОеОЌОЉ ОфОюОф ОъОъОЊОЎ. ОћОДОЋОЉОЎОћ ОћОфОюОф-ОъОъОЊОЎОф ОћОцОаОЎОъОЎОф ОЋОћОДОЋОЉОЎОћ ОћОфОюОф-ОъОъОЊОЎОф ОћОЌОЎОдОЋОаОЎОф ОћОЪ ОћОћОЎОўОюОЎОЮ ОЕОю ОЕОфОЎОЎОЮ ОъОфОЋОџ ОЕОъОЋОаОћ Оћ"ОцОљОЋОф" ОћОфОюОф-ОъОъОЊОЎОЋОф ОЕОю ОћОўОАОеОДОў. ОЕОЕ ОћОцОљОЋОф ОћОљОЌОеОЋОф ОћОцОЏОЋ ОЉОбОДОЉОЋОф ОћОћОўОюОћ ОюОўОеОцОќОЎОЮ ОћОфОюОф-ОъОъОЊОЎОЎОЮ ОЕОъОъОюОљОЎОЮ ОљОф ОћОаОцОЌ ОЕОЉОЎОЪ ОћОДОЋОЉОЎОЋОф.
-
ОљОаОЎОъОдОЎОћ ОЕОю
ОћОЎОўОю ОЕОю ОўОАОеОДОў ОъОќОЋОЋОЎОф ОЕОЋОаОЋОф
-
-
ОћОўОюОћ ОљОюОЏОАОЋОаОЎОф (ОљОа') (ОћОўОюОћ ОъОДОЉОЎОюОЎОф ОЕОљОЎОаОћ ОљОЋОеОфОЋОњОеОцОЎОф) ОЕОю ОћОўОАОеОДОў, ОЕОъОЉОюОЎОўОћ ОљОф ОћОЉОаОЎОЎОћ ОЕОюОЋ ОЏОќОЋОњ ОДОЋОЉОЎОЋОф ОфОюОф-ОъОъОЊОЎОЋОф ОЕОДОЋОЊОДОЋОЊОЎОћОЪ ОћОъОфОљОЎОъОЎОЮ ОъОЌОЋОЉОеОЎОЮ.
[ОЉ]
-
ОћОўОюОћ ОЕОю ОћОўОАОеОДОў ОљОю
ОъОЎОЕОЋОе ОДОЋОДОАОўОе (ОљОа') ОЕОю
ОЌОЉОЋОеОф ОДОЋОДОАОўОе 
, ОЕОљОЎОЉОеОЎОћ ОъОфОљОЎОъОЎОЮ ОюОАОЎОъОўОеОЎОЋОф ОЕОю ОћОўОАОеОДОў. ОћОўОюОћ ОЕОю ОњОЋОцОЎОЮ ОеОЉ-ОъОъОЊОЎОЎОЮ ОљОю ОъОЎОЕОЋОе ОДОЋОДОАОўОе ОЕОю ОЌОЉОЋОеОЋОф ОћОАОЎОъОўОеОЎОћ ОЕОюОћОЮ ОЎОЋОдОеОф ОћОдОњОЋОф ОъОЎОЕОЋОеОЎОЋОф ОбОЮ ОеОъОф ОАОЎОъОўОеОЎОћ ОњОЉОЋОћОћ.
[Оњ]
ОЉОЎОљОЋОеОЎОЮ
- ^ ОћОўОюОћ ОќОЋ ОъОўОЎОюОћ ОљОф ОћОўОАОеОДОў ОћОљОеОЉОб-ОъОъОЊОЎ ОюОфОеОЎОАОеОЋОЪ ОъОбОЋОЎОЎОаОЎ (ОљОа') ОЉОфОюОф-ОъОъОЊ. ОюОЕОЮ ОћОЕОЋОЋОљОћ, ОЉОћОЎОўОю ОЕОю ОДОЋОЉОЎОћ ОфОюОф-ОъОъОЊОЎОф ОЊОеОџ ОдОЎОе ОЕОбОЋОЉОе ОЉОљОюОЏОАОЋОЪ ОеОљОЕОЎ ОЕОюОћ, ОЕОаОЎ ОћОДОЋОЊОДОЋОЊОЎОЮ ОЊОеОЏОЮ ОбОЋОЉОе ОћОдОЎОе ОЎОЋОўОюОЋ ОљОю ОљОЋОфОћ ОаОДОЋОЊОћ ОЉОъОЎОЕОЋОе, ОЉОъОеОЏОќОЋ ОЕОю ОъОЕОЋОЕОћ ОъОЕОЋОЏОюОю, ОЋОЎОфОе ОДОЋОЊОДОЋОЊОЎ ОћОДОЋОЉОЎОћ ОЎОЋОўОюОЋ ОљОю ОЕОЕОф ОДОЋОЊОДОЋОЊОЎ ОћОъОЕОЋОЕОћ; ОЉОЊОЋОъОћ, ОЏОљОЪ ОќОЋОњ ОћОДОЋОЊОДОЋОЊОЎОЮ ОЊОеОЏОЋ ОбОЋОЉОе ОдОЎОе ОћОћОЎОўОю (ОћОДОЋОЊОДОЋОЊОЎОЮ ОћОЎОеОЋОДОЎОЮ) ОљОъОЋОе ОюОћОЎОЋОф ОъОЋОўОю ОљОю ОљОЋОфОћ ОаОДОЋОЊОћ ОЉОъОеОЌОЉ, ОЋОЎОфОе ОћОДОЋОЊОДОЋОЊОЎОЮ РђЋ ОљОю ОљОеОЉОбОћ ОбОЕОе ОћОДОЋОЊОДОЋОЊОЎОЮ ОЕОю ОћОфОеОЎОАОеОЋОЪ ОћОъОбОЋОЎОЎОаОЎ. ОюОўОЋОЉОф ОЉОћОЎОеОЋОф ОћОћОдОњОћ ОЋОћОЎОъОаОбОЋОф ОъОћОфОюОЏОЊОЋОф ОДОЋОЊОДОЋОЊОЎОЮ, ОћОћОўОюОћ ОбОЋОЋОфОћ ОъОбОў ОЋОћОДОЋОЊОДОЋОЊОЎОЮ ОћОъОеОЏОќОЎОЎОЮ ОћОЋОќОќОЋ ОћОдОЎОЊОћ. ОћОДОЋОЊОДОЋОЊОЎОЮ ОћОюОЉОаОЎОЮ ОћОЮ ОљОюОћ ОЕОаОъОдОљОЎОЮ ОЉОъОеОЌОД ОЕОю ОдОюОб ОљОЌОф ОъОћОДОЋОЊОДОЋОЊОЎОЮ ОћОЎОеОЋОДОЎОЮ, ОЋОћОАОњОЋОюОЎОЮ РђЋ ОЉОъОеОЌОД ОЕОфОЎ ОдОюОбОЋОф. ОъОЉОЎОЪ ОћОАОњОЋОюОЎОЮ, ОљОюОћ ОЕОћОЋОўОюОЋ ОљОю ОљОЋОфОЋ ОњОЋОЉОћ (ОЉОъОеОЌОЉ ОћОфОюОф-ОъОъОЊОЎ) ОЕОю ОћОДОЋОЊОДОЋОЊОЎОЮ ОћОЎОеОЋОДОЎОЮ ОаОдОЉОбОЋ ОЉОњОЋОЋОЪ ОЉОћОЎОе ОЎОЋОфОе ОЕОю ОАОњОЋОю. ОЉОЏОю ОћОЊОЎОљОњОеОъОЋОф ОћОАОъОЋОЏОЋОф, ОљОЋОфОЮ ОДОЋОЊОДОЋОЊОЎОЮ ОЉОўОАОеОДОў ОдОЉОЋОбОЎОЮ ОЉОљОЋОфОЮ ОдОЉОбОЎОЮ.
- ^ ОњОЮ ОЉОћОЎОўОю ОћОќОћ ОЋОњОЮ ОЉОћОЎОўОю Оћ-vertex first, ОЕОЎОЕОћ ОбОЕОе ОћОДОЋОЊОДОЋОЊОЎОЮ ОъОАОЋОЊОеОЎОЮ ОЉОЕОЋОеОЋОф ОљОЋОцОДОЎОЋОф, ОЋОЏОъОЋОЎОЋОф ОћОДОЋОЊОДОЋОЊОЎОЮ ОЉОЏОю ОЕОЋОеОћ ОЏОќОЋ ОЕОЋОЋОф ОюОъОАОцОеОЎОЮ ОЕОЉОЕОЋОеОћ 4 ОЉОъОЕОЋОюОЕ ОцОАОДОю.
- ^ ОбОЉОЋОе ОћОўОАОеОДОў ОЕОДОЋОЊОДОЋОЊОЎОЋ ОЉОаОДОЋОЊОЋОф (┬▒1,┬▒1,┬▒1,┬▒1), ОЌОЉОЋОеОф ОДОЋОДОАОўОе ОћОа"Ою ОћОЎОљ ОЌОЉОЋОеОф ОћОАОЎОъОўОеОЎОЋОф ОЕОаОЋОдОеОф ОюОъОЕОю ОбОю ОЎОЊОЎ ОљОеОЉОбОф ОћОЕОЎОДОЋОцОЎОЮ x РЪи -x, x РЪи y, y РЪи z, z РЪи w. ОъОЎОЕОЋОе ОДОЋОДОАОўОе ОЕОю ОћОЌОЉОЋОеОћ ОћОќОЋ ОћОЋОљ ОћОъОЎОЕОЋОе (ОЉОъОеОЌОЉ ОћОљОеОЉОб-ОъОъОЊОЎ) ОЕОфОЋОдОљОф ОћОцОбОюОћ ОАОЊОеОфОЎОф ОЕОю ОЏОю ОћОЎОЋОдОеОЎОЮ ОћОа"Ою ОбОюОЎОЋ ОфОћОЎОћ ОАОЎОЉОЋОЉОЋ ОЉОЕОъОЎОаОЎОф ОАОЎОЉОЋОЉ; 8 ОћОЋОљ ОћОАОЊОе ОЕОю ОљОЎОЉОе ОћОЌОЉОЋОеОћ ОЕОъОфОДОЉОю ОъОћОеОЏОЉОф ОљОеОЉОбОф ОћОЎОЋОдОеОЎОЮ (ОЏОюОЋОъОе ОћОљОЎОЉОе ОЕОцОбОЋОюОфОЋ ОбОю ОћОъОеОЌОЉ ОЕОЋОЋОћ ОюОћОцОбОюОф ОљОеОЉОбОф ОћОЕОЎОДОЋОцОЎОЮ ОћОъОфОљОЎОъОЎОЮ ОЉОќОћ ОљОЌОе ОќОћ). ОћОъОЎОЕОЋОе ОљОъОаОЮ ОфОюОЋОЎ ОЉОЉОЌОЎОеОф ОАОЊОе ОћОцОбОюОф ОћОЎОЋОдОеОЎОЮ, ОљОџ ОЉОЕОю ОћОАОЎОъОўОеОЎОћ ОЕОю ОћОўОАОеОДОў, ОћОћОЎОўОюОЎОЮ ОбОю ОЏОю ОљОЌОЊ ОъОъОЎОЕОЋОеОЎ ОДОЋОДОАОўОе ОћОљОцОЕОеОЎОЎОЮ ОЎОЎОфОаОЋ ОљОф ОљОЋОфОћ ОћОЊОЎОљОњОеОъОћ. ОбОЉОЋОе ОћОАОЊОе ОЉОЋ ОаОЏОфОЉОЋ ОљОеОЉОбОф ОћОЕОЎОДОЋОцОЎОЮ ОюОбОЎОю (ОЏОЕОћОеОљОЕОЋОЪ ОћОЋОљ ОћОЎОцОЋОџ ОЉ-x), ОъОЎОЕОЋОе ОДОЋОДОАОўОе ОћОЋОљ ОћОъОЎОЕОЋОе ОћОаОцОеОЕ ОбОю ОЎОЊОЎ ОћОЋОДОўОЋОеОЎОЮ (1,Рѕџ2,1,0), (0,1,Рѕџ2,1).
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ