Unidade (teoría dos aneis)
|
Read other articles:

Ara bunut Ficus virens Curtain Fig Tree, Atherton TablelandStatus konservasiRisiko rendahIUCN147495192 TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladfabidsOrdoRosalesFamiliMoraceaeGenusFicusSpesiesFicus virens Aiton, 1789 Tata namaSinonim taksonFicus infectoria (Miq.) Miq., Ficus cunninghamiilbs Ficus virens adalah tumbuhan dari genus Ficus yang ditemukan di Pakistan, India, Asia Tenggara, melalui...

Halaman ini berisi artikel tentang sutradara. Untuk pemain sepak bola, lihat Roy Andersson (pemain sepak bola). Roy AnderssonRoy Andersson pada 2014.LahirRoy Arne Lennart Andersson31 Maret 1943 (umur 80)Gothenburg, SwediaKebangsaanSwediaPekerjaanSutradaraTahun aktif1967–sekarang Roy Arne Lennart Andersson (kelahiran 31 Maret 1943) adalah seorang sutradara Swedia, yang paling dikenal karenar A Swedish Love Story (1970) dan trilogi Living-nya, yang meliputi Songs from the Second Flo...

قرية بني ناصر - قرية - تقسيم إداري البلد اليمن المحافظة محافظة حجة المديرية مديرية المحابشة العزلة عزلة حجر السكان التعداد السكاني 2004 السكان 120 • الذكور 58 • الإناث 62 • عدد الأسر 10 • عدد المساكن 6 معلومات أخرى التوقيت توقيت اليمن (+3 غرينيتش) تعد...

Pour les articles homonymes, voir Atmosphère. Atmosphère de Neptune Photo de la Grande tache sombre prise par Voyager 2. Informations générales Épaisseur 8 000 km Composition volumétrique Dihydrogène >84 % Hélium >12 % Méthane 2 % Ammoniac 0,01 % Éthane 0,00025 % Acétylène 0,00001 % modifier L’atmosphère de Neptune est proche de celle d'Uranus. Elle représente entre 5 et 10 % de la masse de la planète et s'étend sur 10 à ...

Canceled NASA Mars rover concept Astrobiology Field LaboratoryAstrobiology Field LaboratoryMission typeAstrobiology roverOperatorNASAWebsiteat jpl.nasa.gov (recovered from archive)Mission duration1 Martian year (proposed) Spacecraft propertiesLaunch mass450 kg (990 lb) maximum Start of missionLaunch date2016 (proposed) The Astrobiology Field Laboratory (AFL) (also Mars Astrobiology Field Laboratory or MAFL) was a proposed NASA rover that would have conducted a search for life...

Chief executive of Zakarpattia Oblast, Ukraine Governor of Zakarpattia OblastIncumbentViktor Mykytasince 10 December 2021ResidenceUzhhorodFormationMarch 24, 1992 as Presidential representative of UkraineWebsiteGovernment of Zakarpattia Oblast The governor of Zakarpattia Oblast (Ukrainian: Закарпатська обласна державна адміністрація, romanized: Zakarpats'ka oblasta derdzavna administratsiya) the head of executive branch for the Zakarpattia Obla...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: 2017 Liberal Democrats deputy leadership election – news · newspapers · books · scholar · JSTOR (January 2018) (Learn how and when to remove this template message) 2017 Liberal Democrats deputy leadership election ← 2014 20 June 2017 2019 → Candidate Jo Swinson Popular vot...

Pour les articles homonymes, voir Toccata (homonymie). Vous lisez un « article de qualité » labellisé en 2020. Dinu Lipatti à l'œuvre sur un piano C. Bechstein. La toccata (de l'italien : toccare, « toucher » ; pl. toccate ; en espagnol : tocar) est, dans la musique baroque, une composition de forme libre pour les instruments à clavier — orgue, clavecin ou piano. Elle est caractérisée par ses figures brillantes, sa virtuosité et son ...

Kabupaten BengkayangKabupatenGapura Selamat Datang LambangJulukan: Bumi SebaloMotto: Adil ka' talino(Dayak) Adil kepada sesama[a]PetaKabupaten BengkayangPetaTampilkan peta KalimantanKabupaten BengkayangKabupaten Bengkayang (Indonesia)Tampilkan peta IndonesiaKoordinat: 1°04′09″N 109°39′50″E / 1.06911°N 109.66393°E / 1.06911; 109.66393Negara IndonesiaProvinsiKalimantan BaratTanggal berdiri27 April 1999Dasar hukumUndang-undang RI Tahun 1...

Kurva sinus topologis, contoh berguna dalam topologi point-set. Hal ini terhubung tapi tidak jalan-terhubung.Dalam matematika, topologi umum adalah cabang dari topologi yang berhubungan dengan definisi dan konstruksi teori himpunan dasar yang digunakan dalam topologi. Ini adalah dasar dari sebagian besar cabang lain dari topologi, termasuk topologi diferensial, topologi geometris, dan topologi aljabar. Nama lain untuk topologi umum adalah topologi himpunan-titik. Konsep dasar dalam topologi h...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Jewish German physician and sexologist (1868–1935) Magnus HirschfeldHirschfeld in 1932Born(1868-05-14)14 May 1868Kolberg, Kingdom of Prussia, North German Confederation(now Kołobrzeg, Poland)Died14 May 1935(1935-05-14) (aged 67)Nice, FranceResting placeBody cremated; ashes interred in Caucade Cemetery in NiceCitizenshipGerman (revoked by the Nazis)[1]OccupationPhysicianKnown forInstitut für Sexualwissenschaft, Scientific Humanitarian Committee, World League for Sexual Re...

Propriétés des systèmes isolés, fermés et ouverts dans l'échange d'énergie et de matière. Un système isolé, par opposition à un système ouvert, est un système physique qui n'interagit pas avec ses environnements. On dit d’un système qu’il est isolé s’il n'échange ni matière, ni chaleur, ni travail avec l'extérieur (paroi adiabatique et indéformable) – un système fermé peut échanger de la chaleur ou du travail avec l'extérieur, mais pas de la matière. Ce systèm...

Aspect of the COVID-19 outbreak Part of a series on theCOVID-19 pandemicScientifically accurate atomic model of the external structure of SARS-CoV-2. Each ball is an atom. COVID-19 (disease) SARS-CoV-2 (virus) Cases Deaths Timeline 2019 2020 January responses February responses March responses April responses May responses June responses July responses August responses September responses October responses November responses December responses 2021 January responses February responses March r...

Не следует путать с другими международными судами в Гааге. Международный уголовный судCour pénale internationale International Criminal Court Эмблема суда Вид международный судебный орган Инстанция суд высшей инстанции Юрисдикция Государства-участники Римского статута Дата основания 17 июля 1...

This is a list of University of Dhaka alumni and faculty members. Politicians Sheikh Mujibur Rahman, 1st and 4th President and Father of the Nation of Bangladesh Syed Nazrul Islam, former acting President of Bangladesh during the Bangladesh Liberation War in 1971 Mohammad Mohammadullah, 3rd President of Bangladesh Khondaker Mostaq Ahmad, 5th President of Bangladesh A. F. M. Ahsanuddin Chowdhury, 9th President of Bangladesh Hussain Muhammad Ershad, 10th President of Bangladesh Abdur Rahman Bi...

Morda RoadGround informationLocationOswestry, ShropshireEstablishment1964 (first recorded match)Team information Shropshire (1964-1980 & 1990-present)As of 15 August 2010Source: Ground profile Morda Road is a cricket ground in Oswestry, Shropshire. The first recorded match on the ground was in 1964, when Shropshire played their first Minor Counties Championship match at the ground against the Somerset Second XI. From 1964 to 2000, the ground hosted 18 Minor Counties Championship matches....

Pour les articles homonymes, voir Lalanne. René ManzorRené ManzorBiographieNaissance 4 août 1959 (64 ans)Mont-de-MarsanNom de naissance René LalannePseudonyme René ManzorNationalité FrançaiseActivités Scénariste, écrivain, réalisateur, scénariste de cinémaFratrie Francis LalanneJean-Félix LalanneAutres informationsSite web renemanzor.comFilms notables Le Passage3615 code Père NoëlUn amour de sorcièreDédalesmodifier - modifier le code - modifier Wikidata René Lalanne, ...

Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Moïse apercevant la Terre promise, F. E. Church, 1846. Origine religieuse Article détaillé : Terre promise (religion). Carte de Canaan, 1869. Judaïsme La Terre promise (hé. הארץ המובטחת, translit.: ha'aretz hamuvtakhat) représente ce que dès la Genèse, la Torah (Bible hébraïque) désigne sous le nom de « Terre d'Israël » dans le pays de Canaan, « pays ...
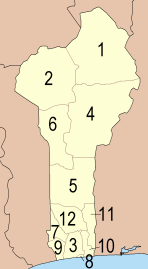
У этого термина существуют и другие значения, см. Бенин (значения). Республика Бенинфр. République du Bénin Флаг Герб Девиз: «Fraternité, Justice, Travail(с фр. — «Братство, Справедливость, Труд»)» Гимн: «L'Aube Nouvelle» Бенин на карте мира Дата независимости 1 августа 1960 года (от Франци...









![{\displaystyle R[[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aacb21250f99f332a57763ecb7f92e3637ade19)









![{\displaystyle \mathbb {G} _{m}(R)\simeq \operatorname {Hom} (\mathbb {Z} [t,t^{-1}],R)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c7385d9d048f7923fa85690937000b3e2b015cd)
![{\displaystyle \mathbb {Z} [t,t^{-1}]\to R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/097602f428d486a9ea02003085c0fddf8b8a4ee6)
![{\displaystyle \mathbb {Z} [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e65744a826d17b7e9fa264dc341006b9be5d55)
