Lista de sumas de recíprocos
|
Read other articles:

Keuskupan OberáDioecesis OberensisDiócesis de OberáKatolik Katedral Santo Antonius dari PaduaLokasiNegaraArgentinaProvinsi gerejawiCorrientesStatistikLuas78.074 km2 (30.145 sq mi)Populasi- Total- Katolik(per 2012)275.100203,800 (74.1%)Paroki17InformasiDenominasiKatolik RomaRitusRitus RomaPendirian13 Juni 2009 (14 tahun lalu)KatedralKatedral Santo Antonius dari Padua di OberáKepemimpinan kiniPausFransiskusUskupDamián Santiago BitarUskup agungAndrés Stan...

Artikel ini sebagian besar atau seluruhnya berasal dari satu sumber. Diskusi terkait dapat dibaca pada the halaman pembicaraan. Tolong bantu untuk memperbaiki artikel ini dengan menambahkan rujukan ke sumber lain yang tepercaya.Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Pelantikan Bacha...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

His EminenceJoão Braz de AvizCardinal Prefect of the Congregation for Institutes of Consecrated Life and Societies of Apostolic LifeAppointed4 January 2011PredecessorFranc RodeOther post(s)Cardinal priest of Sant’Elena fuori Porta PrenestinaOrdersOrdination26 November 1972by Romeu AlbertiConsecration31 May 1994by Domingos Gabriel WisniewskiCreated cardinal18 February 2012by Pope Benedict XVIRankCardinal deacon (2012–22)Cardinal priest (2022–present)Personal detailsBornJoão ...

Main article: 2024 United States presidential election 2024 United States presidential election in Wyoming ← 2020 November 5, 2024 2028 → Nominee Donald Trump(presumptive) Joe Biden(presumptive) Party Republican Democratic Home state Florida Delaware Running mate TBA Kamala Harris(presumptive) Incumbent President Joe Biden Democratic Elections in Wyoming Federal government Presidential elections 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 193...

La barcaLa barca, I ed, Guanda, Modena 1935 AutoreMario Luzi 1ª ed. originale1935 Genereraccolta poetica Lingua originaleitaliano Modifica dati su Wikidata · Manuale La barca è la prima raccolta poetica di Mario Luzi pubblicata nel 1935 a Modena dall'editore Guanda. Indice 1 Storia editoriale 2 Influenze 3 Tematiche e contenuti 4 Lingua e stile 5 Edizioni 6 Note 7 Bibliografia Storia editoriale Alla prima edizione del 1935 ne seguirono una seconda nel 1942 e quella definitiva del 1960...

Bahasa SundaBPS: 0086 6 Basa Sundaᮘᮞ ᮞᮥᮔ᮪ᮓ • باسا سوندا Tulisan Sunda dalam aksara Sunda Baku Pengucapan[basa sʊnda] (standar)[basa suna] (vernakular)Dituturkan diIndonesia serta negara-negara dengan diaspora SundaWilayahUtamanya bagian barat Pulau Jawa dan provinsi lainnya di IndonesiaEtnisSunda(Badui • Banten • Ciptagelar • Cirebon • Priangan)Penutur42 juta (2016)[1] Rincian data penutur Jumlah penutur beserta (jik...

Location of KazakhstanWine making in Kazakhstan Kazakh wine is wine made in Kazakhstan. The roots of the Kazakh wine industry can be traced to the 7th century AD when grapevines were brought to the region from neighboring Uzbekistan and China. While only around 4% of the land in Kazakhstan is ideally situated for viticulture, the country does manage to produce over 6.2 million gallons (236,000 hl) of wine annually from 32,120 acres (13,000 ha).[1] Buoyed by its mineral wealth, th...

Season of television series Winx ClubSeason 3 Italian DVD cover (left) and artwork from the 2011 re-release (right)No. of episodes26ReleaseOriginal networkRai Due, 4Kids TV, NickelodeonOriginal release29 January (2007-01-29) –28 March 2007 (2007-03-28)Season chronology← PreviousSeason 2Next →Season 4List of episodes The third season of the animated series Winx Club aired from 29 January to 28 March 2007, consisting of 26 episodes. The series was created by Igin...

Torquay United 1929–30 football seasonTorquay United1929–30 seasonChairman Charles DearManager Frank WomackThird Division South19thFA CupFirst RoundTop goalscorerLeague: Joe Pointon (18)All: Joe Pointon (18)Highest home attendance8,299 v Plymouth Argyle, 4 September 1929 (Third Division South)Lowest home attendance2,730 v Watford, 28 December 1929 (Third Division South)Average home league attendance4,271 Home colours ← 1928–291930–31 → The 1929–30 Torquay Unit...

Mie baksoSemangkuk mie baksoNama lainMi bakso, mee bakso, bakso meeSajianHidangan utama (makan siang)Tempat asalIndonesiaDaerahSeluruh negeri di Indonesia, juga populer di negara-negara tetangga Asia TenggaraDibuat olehTionghoa Indonesia, Jawa dan MelayuSuhu penyajianPanasSunting kotak info • L • BBantuan penggunaan templat ini Mie bakso adalah sebuah hidangan sup bakmi Indonesia yang terdiri dari bakso yang disajikan dengan mi kuning dan bihun. Mie bakso nyaris identik dengan s...

Thompson v ParkCourtCourt of AppealDecided28 February 1944Citation(s)[1944] KB 408KeywordsLicence; revoked; possible breach of joint venture contract; whether forcible re-entry trespass; whether re-entry proper for right to sue for damages in a non-commercial, school context Thompson v Park [1944] KB 408 is an English law case, concerning licenses in land. Facts Mr. Thompson, the school's headmaster, wanted an injunction for Mr. Park to leave his school, after Mr. Park had forced his way bac...

This image is usually interpreted as a Valkyrie who welcomes a dead man, or Odin himself, on the Tjängvide image stone from Gotland, in the Swedish Museum of National Antiquities in Stockholm. Death in Norse paganism was associated with diverse customs and beliefs that varied with time, location and social group, and did not form a structured, uniform system. After the funeral, the individual could go to a range of afterlives including Valhalla (a hall ruled by Odin for the warrior elite wh...

ورم الغدة الجار درقية ورم الغدة الجار درقيةورم الغدة الجار درقية تسميات أخرى ورم الغدة الجار درقية معلومات عامة الاختصاص علم الأورام من أنواع نمط خلوي لورم حميد [لغات أخرى]، وورم غدي، ومرض المظهر السريري الأعراض أعراض فرط نشاط جارات الدرق (كسور عظمي�...
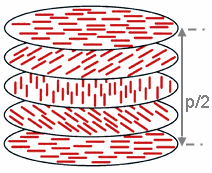
Холестерический жидкий кристалл Холестерические жидкие кристаллы (ХЖК), холестерики — жидкие кристаллы со спиральными молекулами, в них отсутствует центральная симметрия, они имеют свойство хиральности. Холестерическая фаза существует только у веществ, молекулы ко...

Le E3 Långa, ou E3 (longue distance), est le nom de deux courses hippiques de trot attelé se déroulant fin juin, début juillet sur l'hippodrome de Färjestad (sv), en Suède (hippodrome de Bergsåker en 2023). Ce sont des courses internationales de Groupe I réservées aux chevaux de 3 ans, hongres et mâles pour l'une, femelles pour l'autre. Elles se courent sur la distance de 2 140 mètres, départ à l'autostart, avec pour chacune une allocation qui s'élève à 2 0...

Organic compound with acidic properties This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Organic acid – news · newspapers · books · scholar · JSTOR (April 2009) (Learn how and when to remove this message) Acids and bases Acceptor number Acid Acid–base reaction Acid–base homeostasis Acid strength Acidity f...

Weekly Shōnen MagazineKategoriManga shōnen[1][2]FrekuensiMingguanSirkulasi883.804[1](Juli–September 2016)PenerbitKodanshaTerbitan pertama17 Maret 1959; 65 tahun lalu (1959-03-17)NegaraJepangBahasaJepangSitus webShōnen Magazine Weekly Shōnen Magazine (Jepang: 週刊少年マガジンcode: ja is deprecated , Hepburn: Shūkan Shōnen Magajin) adalah sebuah majalah antologi manga shōnen mingguan yang diterbitkan di Jepang oleh Kodansha, dan pertama kali diterb...

Johannes Bah Kuhnke nel 2009 Kjell Dietrich Johannes Bah Kuhnke, noto come Johannes Bah Kuhnke o Johannes Kuhnke (Strömsund, 17 aprile 1972), è un attore e cantante svedese.[1] Ha recitato in diversi film e spettacoli teatrali, acquisendo notorietà internazionale per la sua interpretazione nel film Forza maggiore, presentato al 67º Festival di Cannes. Nel 2010 ha partecipato come cantante alla competizione canora del Melodifestivalen, con il brano Tonight.[2] Indice 1 Biog...

Campionati europei a squadre di atletica leggeraSport Atletica leggera TipoSquadre nazionali CategoriaSeniores FederazioneEAA ContinenteEuropa OrganizzatoreEuropean Athletic Association TitoloCampione europeo a squadre CadenzaBiennale Sito Interneteuropean-athletics.com StoriaFondazione2009 Numero edizioni10 (al 2023) Detentore Italia Record vittorie Germania (5 titoli) Ultima edizione2023 Prossima edizione2025 Modifica dati su Wikidata · Manuale I Campionati europei a squadre di atleti...

























