Ciaxares
| ||||||||||||||||||||||||||||||||||||||||
Read other articles:

Biskuit butir cokelatSebuah biskuit butir cokelatSajianMakanan penutup atau makanan ringanTempat asalAmerika SerikatDaerahWhitman, MassachusettsDibuat olehRuth Graves Wakefield, Toll House InnDiciptakan tahun1938Bahan utamaTepung, gula, gula cokelat, mentega atau margarin, butir cokelat, telur, vanilla, soda kue, garamVariasiBanyak, termasuk menambahkan kacang, havermut, selai kacangSunting kotak info • L • BBantuan penggunaan templat ini Buku resep: Biskuit butir cokelat ...

Ini adalah macam-macam medsos yang sering di gunakan Pemasaran dengan media sosial (bahasa Inggris: social media marketing) adalah proses meraih kunjungan pengguna internet ke situs tertentu atau perhatian khalayak ramai melalui situs-situs sosial media.[1] Kegiatan pemasaran dengan menggunakan media sosial biasanya berpusat pada usaha sebuah perusahaan untuk menciptakan konten yang menarik perhatian, sehingga mendorong para pembaca untuk membagikan konten tersebut melalui jejaring me...

Mantel Arma Kerajaan Britania RayaVersionsMantel Arma Kerajaan Britania Raya untuk penggunaan di SkotlandiaDetailPemangkuCharles IIIDigunakan sejak1837MustakaSinga aurum dengan mahkota yang berdiri di atas mahkota kerajaan; Mantel cerpelai berbalut aurumPerisaiKuartal: 1 dan 4 Inggris, 2 Skotlandia, 3 IrlandiaPenopangSinga aurum dan kuda ekacula fidahKompartemenTudor rose, Shamrock, dan ThistleMottoDieu et mon droit (di luar Skotlandia)Nemo me impune lacessit (di Skotlandia)Tanda kehormatanOr...

Cet article est une ébauche concernant un homme politique uruguayen. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Reinaldo GarganoReinaldo GarganoFonctionsMinistre des Affaires étrangèresSénateur de l'UruguayBiographieNaissance 26 juillet 1934PaysandúDécès 5 février 2013 (à 78 ans)MontevideoSépulture Parque del Recuerdo (en)Nationalité uruguayenneActivités Diplomate, homme politiqueAutres inf...

The mathematics of smooth surfaces Riemannian surface redirects here. Not to be confused with Riemann surface. Carl Friedrich Gauss in 1828 In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties det...

Voce principale: Associazione Calcistica Perugia Calcio. Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Associazione Calcio PerugiaStagione 1963-1964I grifoni col secondo completo bianco Sport calcio Squadra Perugia Allenatore Domenico Bosi, poi Aroldo Collesi Presidente Orlando Baldoni Serie C - Gir. B12º posto Miglior marc...

Abandoned whaling town in Canada Abandoned Whaling Town in Newfoundland and Labrador, CanadaRose au Rue RosiruAbandoned Whaling TownRose au Rue Whaling Station, 1942Rose au RueLocation of Rose au Rue in NewfoundlandCoordinates: 47°31′00″N 54°10′57″W / 47.51667°N 54.18250°W / 47.51667; -54.18250Country CanadaProvince Newfoundland and LabradorCensus divisionDivision 1Census subdivisionSubdivision BPopulation (1945) • Total5[1 ...

Міністерство оборони України (Міноборони) Емблема Міністерства оборони та Прапор Міністерства оборони Будівля Міністерства оборони у КиєвіЗагальна інформаціяКраїна УкраїнаДата створення 24 серпня 1991Попередні відомства Міністерство оборони СРСР Народний комісарі...

6th Congress of the PhilippinesJanuary 17, 1966 – June 17, 1969PresidentFerdinand MarcosVice PresidentFernando LopezSenateSenate President Gil J. PuyatSenate Presidentpro tempore Jose J. RoyMajority leader Jose J. RoyRodolfo T. GanzonArturo TolentinoMinority leaderAmbrosio PadillaHouse of RepresentativesHouse SpeakerCornelio VillarealJose B. Laurel, Jr.Majority leaderJustiniano S. MontanoMarcelino VelosoMinority leaderJosé B. Laurel, Jr.◄ 5th (1962)7th (1970) ► Politi...

فرديناندو دي ميديشي معلومات شخصية الميلاد 9 أغسطس 1663(1663-08-09)فلورنسا الوفاة 31 أكتوبر 1713 (50 سنة)فلورنسا سبب الوفاة زهري مكان الدفن كنيسة القديس لورينزو الديانة كاثوليكية عضو في أكاديمية كروسكا مشكلة صحية صرع الزوجة فيولانتي بياتريس من بافاريا [لغات أخرى]R...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Ruinas de la catedral de San Pablo de Macao patrimonio de influencia portuguesa y Patrimonio de la Humanidad LocalizaciónPaís República Popular ChinaImperio portuguésDivisión MacaoCoordenadas 22°11′51″N 113°32′27″E / 22.197468, 113.54086Información religiosaCulto catolicismoDiócesis Diócesis de MacaoOrden Compañía de JesúsAdvocación TheotokosHistoria del edificioFundación 1602Fundador Carlos SpinolaArquitecto Carlos SpinolaMapa de localización Ruinas de...

The BarbershopSutradaraWilliam K.L. Dickson dan William HeisePerusahaanproduksiPerusahaan Manufaktur EdisonTanggal rilis1894Durasi22 detik The Barbershop adalah sebuah film naratif pendek Amerika Serikat tahun 1894 garapan William K.L. Dickson dan William Heise. Film tersebut diproduksi oleh Perusahaan Manufaktur Edison di Studio Black Maria, West Orange, New Jersey. Film ini adalah salah satu yang pertama kali dibuat untuk Kinetoskop.[1] Alur cerita Di sebuah barbershop, seorang tuka...

Bolbeno abolished municipality in Italy (en) Frazione Bolbeno (it) Tempat Negara berdaulatItaliaDaerah otonom dengan status istimewaTrentino-Tirol SelatanProvinsi di ItaliaTrentinoKomune di ItaliaBorgo Lares (en) NegaraItalia Ibu kotaBolbeno PendudukTotal352 (2008 )GeografiLuas wilayah12 km² [convert: unit tak dikenal]Ketinggian585 m Berbatasan denganBleggio Superiore Sella Giudicarie (en) Preore Zuclo Tione di Trento Bondo, Italia Breguzzo SejarahSanto pelindungZeno Informasi tam...

此条目页介紹的是有線電視廣播系統。 關於香港的有線電視有限公司,請見「香港有線電視」。 關於澳門的有線電視有限公司,請見「澳門有線電視」。 關於台灣的有線電視有限公司,請見「第四台」。 此條目已列出參考文獻,但因為沒有文內引註而使來源仍然不明。 (2021年5月14日)请加上合适的文內引註来改善这篇条目。 一條普通(RG-59)的同軸電纜 A:電線外�...

New Zealand government led by Jim Bolger and Jenny Shipley respectively from 1990 to 1999 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fourth National Government of New Zealand – news · newspapers · books · scholar · JSTOR (June 2011) (Learn how and when to remove this message) Fourth National GovernmentM...

Adult contemporary radio station in Wichita, Kansas KRBBWichita, KansasBroadcast areaWichita metropolitan areaFrequency97.9 MHz (HD Radio)BrandingB98ProgrammingFormatAdult contemporarySubchannelsHD2: Contemporary hit radio Kiss RadioAffiliationsPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsKTHR, KZCH, KZSNHistoryFirst air dateSeptember 19, 1948; 76 years ago (1948-09-19) (as KFH-FM)Former call signsKFH-FM (1948–1971)KBRA (1971–1982)KLZ...
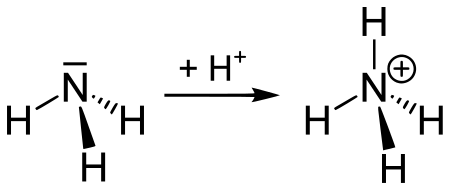
Dieser Artikel behandelt das chemische Kation. Zu der ägyptischen Orakelstätte des Ammon siehe Orakel von Siwa. Bildung eines Ammonium-Ions durch Protonierung von Ammoniak. Salmiaknebel beim Zusammentreffen von Ammoniak- und Salzsäuredämpfen Das Ammonium-Ion NH4+ (nach IUPAC auch Azanium-Ion[1]) ist ein Kation, das sich in einer Säure-Base-Reaktion aus der gasförmigen Base Ammoniak durch Anlagerung eines Protons an das freie Elektronenpaar bildet. Damit ist aus chemischer Sicht...

Planisferio de Caverio. El planisferio de Caverio o Canerio,[1] fue dibujado entre 1504-1505 por el cartógrafo genovés Nicolaus de Caverio o Nicolo Caveri, representando el mundo conocido por los occidentales en 1502-1504. Toma como modelo el Planisferio de Cantino, ligeramente actualizado, con la mayor parte de sus anotaciones topográficas en portugués. Se conserva en el Departamento de mapas y planos de la Biblioteca Nacional de Francia. Descripción El planisferio consta de diez...

متحف المنحوتات في شحات إحداثيات 32°49′04″N 21°51′51″E / 32.817639°N 21.864167°E / 32.817639; 21.864167 معلومات عامة الدولة ليبيا معلومات أخرى تعديل مصدري - تعديل الحسان الثلاثة في متحف شحات. متحف شحات أو متحف المنحوتات في شحات في ليبيا. هو متحف قرب مدينة قوريني التاريخي�...