Transformée de Hadamard
|
Read other articles:

Concours Eurovision de la chanson 1963 Dates Finale 23 mars 1963 Retransmission Lieu BBC Television CentreLondres, Royaume-Uni Présentateur(s) Katie Boyle Directeur musical Eric Robinson Télédiffuseur hôte BBC Ouverture Vues de Londres Entracte Ola et Barbro Participants Nombre de participants 16 Débuts Aucun Retour Aucun Retrait Aucun Pays participants Résultat Chanson gagnante Dansevisepar Grethe & Jørgen Ingmann Danemark Système de vote Un jury par pays, composé de 20 membres...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) البطولة الوطنية المجرية 1969 تفاصيل الموسم البطولة الوطنية المجرية النسخة 68 البلد المجر المنظم �...

Pour les articles homonymes, voir Parterre. Parterres à Waddesdon Manor, en Angleterre Un parterre est la partie dégagée et plane d'un jardin d'agrément ou d'un parc formant par sa composition un ensemble décoratif. Régulièrement divisé par des allées en compartiments et en plates-bandes bordés de pierre ou de haies rigoureusement taillées, il est essentiellement garni de fleurs, herbes et arbustes. Généralement situé face au bâtiment principal d'une résidence ou à l'intéri...

American actress and painter (1910–2010) Gloria Stewart redirects here. For Jimmy Stewart's wife, see Gloria Hatrick McLean. Gloria StuartStuart in 1937BornGloria Stewart(1910-07-04)July 4, 1910Santa Monica, California, U.S.DiedSeptember 26, 2010(2010-09-26) (aged 100)Los Angeles, California, U.S.Other names Gloria Finch Gloria Frances Stuart Alma materUniversity of California, BerkeleyOccupationsActressartistfine printerYears active1927–2004WorksFilmographyPolitical p...

Indian Ruling Dynasty Chitradurga Nayaka Kingdom Official language Telugu, Kannada Capitals Chitradurga Government Monarchy Preceding state Vijayanagar Empire Succeeding states Kingdom of Mysore Nayakas of Chitradurga (1588–1779 CE) ruled parts of eastern Karnataka during the post-Vijayanagara period. During the rule of Hoysala Empire and Vijayanagara Empire, they served as a feudatory chiefdom. Later, after the fall of the Vijayanagara empire, they ruled at times as an independent chiefdom...

Jacksonville Tea MenCalcio The Tea Men Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Arancione, bianco, rosso Simboli Veliero Casa Trasferta Dati societari Città Jacksonville, FL Nazione Stati Uniti Confederazione CONCACAF Federazione USSF Campionato NASLASL Fondazione 1981 Scioglimento1984 Stadio Gator Bowl Stadium, Jacksonville FL( posti) Palmarès Si invita a seguire il modello di voce I Jacksonville Tea Men furono un club calcistico statunitense di Jacksonville (...

Disambiguazione – Se stai cercando l'album di Fler, vedi Neue Deutsche Welle (album). Questa voce o sezione sull'argomento musica è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i s...

Masjid KubelieMasjid Kapllan PashaXhamia e KubeliesëXhamia e Kapllan PashësMasjid Kubelie di pusat Kota KavajëAgamaAfiliasiIslamLokasiMunisipalitasKavajëNegaraAlbaniaKoordinat41°11′01″N 19°33′43″E / 41.1837035°N 19.561852°E / 41.1837035; 19.561852Koordinat: 41°11′01″N 19°33′43″E / 41.1837035°N 19.561852°E / 41.1837035; 19.561852ArsitekturGaya arsitekturArsitektur Islam UtsmaniyahDidirikan1735SpesifikasiKubah1Menara1 M...

American racing driver (born 1996) NASCAR driver Bayley CurreyCurrey at Martinsville Speedway in 2024BornBayley Alexander Currey (1996-10-29) October 29, 1996 (age 27)Driftwood, Texas, U.S.Achievements2014 Viper Pro Late Model Series ChampionNASCAR Cup Series career12 races run over 3 years2021 position64thBest finish52nd (2019)First race2019 TicketGuardian 500 (Phoenix)Last race2021 Quaker State 400 (Atlanta) Wins Top tens Poles 0 0 0 NASCAR Xfinity Series career111 races run over 6 yea...

Auto race Firecracker 250 redirects here. For the NASCAR Cup Series race at Daytona from 1959 to 1962, see Coke Zero Sugar 400. Wawa 250NASCAR Xfinity SeriesVenueDaytona International SpeedwayLocationDaytona Beach, Florida, United StatesCorporate sponsorWawa, Coca-ColaFirst race2002Distance250 miles (400 km)Laps100Stages 1/2: 30 eachFinal stage: 40Previous namesStacker 2/GNC Live Well 250 (2002)Winn-Dixie 250 (2003)Winn-Dixie 250 presented by PepsiCo (2004–2007)Winn-Dixie 250 Powered b...

ريدون آر 200 (بالإنجليزية: Radeon R200) وهو ثاني جيل من سلسلة ريدون من وحدات معالجة الرسوميات في شركة إيه تي آي.[1][2][3] وهي السلسلة التي أمّنت استمرارية شركة إي تي آي في حين كان معظم وحدات معالجة الرسوميات التابعة لشركات أخرى تبوء بالفشل، ورفعتها إلى مستوى متعادل مع شر...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Mist-based plant growing process This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (March 2018) (Learn how and when to remove this message) This article contains content that is written like an advertisement. Please help improve ...

Gaeltachtaí på Irland En gaeltacht (i plural gaeltachtaí) är ett område där iriska är förstaspråk.[1] Termen förekommer oftast i singular och används dels kollektivt om hela det irisktalande området, dels om enskilda geografiska områden. I republiken Irland finns statligt fastslagna geografiska områden där iriska är officiellt erkänt som majoritetsspråk, framförallt i den västra delen av landet.[2] Men termen gaeltacht används också i en vidare mening om iriskspråkiga o...

Overview of the events of 1932 in film Overview of the events of 1932 in film List of years in film … 1922 1923 1924 1925 1926 1927 1928 1929 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940 1941 1942 … In television 1929 1930 1931 1932 1933 1934 1935 In radio 1929 1930 1931 1932 1933 1934 1935 In music 1929 1930 1931 1932 1933 1934 1935 Art Archaeology Architecture Literature Music Philosophy Science +... Years in film 19th century 1870s 1880s 1880 1881 1882 1883 1884 1885 1886 18...

Cet article est une ébauche concernant un acteur portugais. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les conventions filmographiques. João VillaretBiographieNaissance 10 mai 1913LisbonneDécès 21 janvier 1961 (à 47 ans)LisbonneNom de naissance João Henrique Pereira VillaretNationalité portugaiseActivité ActeurAutres informationsDistinctions Grand officier de l'ordre de Sant'Iago de l'ÉpéeOfficier de l'ordre de Sant'Iago de l'Épéemodifie...

Hakuin Ekaku GelarRōshiInformasi pribadiLahirsekitar 1686JepangMeninggalsekitar 1769MazhabRinzai Ini adalah nama Jepang, nama keluarganya adalah Hakuin. Hakuin Ekaku (白隠 慧鶴code: ja is deprecated , 19 Januari 1686 - 18 Januari 1768) adalah salah satu figur paling berpengaruh dalam Buddha Zen Jepang. Biografi Tahun-tahun awal Hakuin lahir pada 1686 di desa kecil Hara,[web 1] di kaki Gunung Fuji. Penulisan Hakuin (2005), The Five Ranks. In: Classics of Buddhism and Zen. The Coll...

City-state in ancient Sumer Not to be confused with Queen Larsa of the video game Mushihimesama Futari. Larsa𒌓𒀕𒆠{{{1}}}Shown within IraqLocationIshan al-Bahriyat, Al-Qādisiyyah Governorate, IraqRegionMesopotamiaCoordinates31°17′9″N 45°51′13″E / 31.28583°N 45.85361°E / 31.28583; 45.85361TypeSettlement Mesopotamia in the time of Hammurabi Larsa (Sumerian: 𒌓𒀕𒆠, romanized: UD.UNUGKI,[1] read Larsamki[2]), also referred to...

Gibraltar has a limited public transport system, due to the compact size of the territory. Road Private transport Traffic drives on the right Gibraltar's country identifier is GBZ A current Gibraltar rear number plate featuring the country identifier GBZ Gibraltar has 49.9 kilometres (31.0 mi) of highways, all of which are paved. It has one of the highest levels of per capita car ownership in the world, with as many motor vehicles as people. Unlike the United Kingdom, along with the Bri...
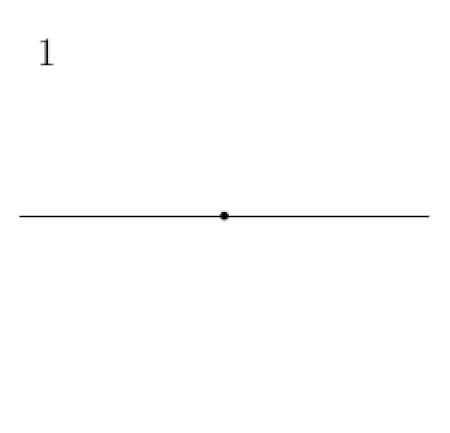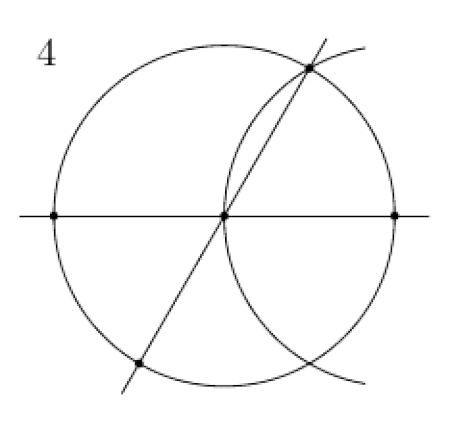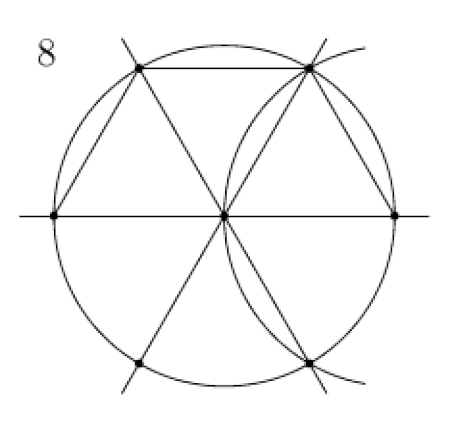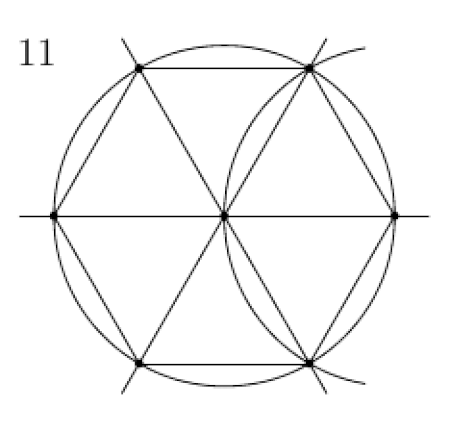
Hình họcHình chiếu một mặt cầu lên mặt phẳng. Đại cươngLịch sử Phân nhánh Euclid Phi Euclid Elliptic Cầu Hyperbol Hình học phi Archimedes Chiếu Afin Tổng hợp Giải tích Đại số Số học Diophantos Vi phân Riemann Symplectic Phức Hữu hạn Rời rạc Kỹ thuật số Lồi Tính toán Fractal Liên thuộc Khái niệmChiều Phép dựng hình bằng thước kẻ và compa Đỉnh Đường cong Đường chéo Góc Song song Vuông góc ...


















