Théorie de Ramsey
|
Read other articles:

Human toll of the Syrian civil warGraphs are unavailable due to technical issues. There is more info on Phabricator and on MediaWiki.org.Pre-war population 22 ±.5; Internally displaced 6 ±.5, Refugees 5.5 ±.5, Fatalities 0.5 ±.1 (millions)[citation needed]Syrian refugees By countryEgypt, Lebanon, Jordan, TurkeySettlementsCamps: Jordan Internally displaced Syrians Casualties of the war CrimesHuman rights violations, massacres, rape Return of refugees, Refugees as weapons, Prosecuti...

David ResnickDavid Resnick, Arsitek dan Perencana Tata KotaLahir(1924-08-05)5 Agustus 1924Rio de Janeiro, BrasilMeninggal4 November 2012(2012-11-04) (umur 88)KebangsaanIsraelPekerjaanArsitekPenghargaanPenghargaan Israel; Penghargaan RechterPraktikDavid Reznik Baruch Reznik Architects & Town PlannersGedungSinagoge Rabbi Dr. I. GoldsteinJerusalem Hyatt RegencyYad Kennedy David Resnick (Ibrani: דוד רזניקcode: he is deprecated ; 5 Agustus 1924 – 4 November 2012&#...

Margrethe IIRatu Margrethe II pada Mei 2012Ratu DenmarkBerkuasa14 Januari 1972 – 14 Januari 2024(52 tahun, 0 hari)PendahuluFrederik IXPenerusFrederik XPerdana Menteri Lihat daftar Denmark Jens Otto KragAnker JørgensenPoul HartlingPoul SchlüterPoul Nyrup RasmussenAnders Fogh RasmussenLars Løkke RasmussenHelle Thorning-SchmidtMette Frederiksen Kepulauan Faroe Atli DamJógvan SundsteinMarita PetersenEdmund JoensenAnfinn KallsbergJóannes EidesgaardKaj Leo JohannesenAksel V. J...

Kedutaan Besar Republik Indonesia di Abu DhabiKoordinat24°26′06″N 54°22′17″E / 24.435°N 54.371519°E / 24.435; 54.371519Lokasi Abu Dhabi, Uni Emirat ArabAlamatZone 2, Sector 79, Villa No. 819Sultan bin Zayed Street(Street 32)Al Bateen Area, Abu DhabiUni Emirat ArabDuta BesarHusin BagisSitus webkemlu.go.id/abudhabi/id Kedutaan Besar Republik Indonesia di Abu Dhabi (KBRI Abu Dhabi) adalah misi diplomatik Republik Indonesia untuk Uni Emirat Arab (UEA).[1 ...

American poet Jen HoferHofer in 2020Born1971San FranciscoNationalityAmericanOccupation(s)American poet and translatorOrganizationAntena-AireAwardsPEN Award for Poetry in Translation; Harold Morton Landon Translation AwardWebsitehttp://antenaantena.org/about-us-2/ Jen Hofer (born 1971[1]) is an American poet, translator, and interpreter. Awards Hofer won the 2012 PEN Award for Poetry in Translation, for the poem Negro Marfil/Ivory Black.[2] The PEN Award judges refer to Hofer's...

PersepamNama lengkapPersepam PamekasanJulukan Laskar Ronggo Sukowati The Angry Bull Berdiri1970StadionStadion Gelora Ratu PamelinganKabupaten Pamekasan, Madura(Kapasitas: 20,000)PemilikAsosiasi PSSI Kab. PamekasanKetua Umum Djohan SusantoManajer Djohan SusantoPelatih Mohammad Romli EfendiLigaLiga 3Kelompok suporterTaretan Mania, Kancah Mania, Pamekasan X Fans, Tretan Dhibik Kostum kandang Kostum tandang Kostum ketiga Persepam Pamekasan merupakan klub sepak bola profesional di Indonesia yang b...

Sporting event delegationPakistan at the2006 Asian GamesIOC codePAKNOCPakistan Olympic Associationin DohaCompetitors387MedalsRanked 31st Gold 0 Silver 1 Bronze 3 Total 4 Asian Games appearances (overview)195419581962196619701974197819821986199019941998200220062010201420182022 Pakistan competed in the 2006 Asian Games held in Doha, Qatar. Medalists [1] Medal Name Sport Event Date Silver Muhammad AkramNasir AliBadshah GulWajid AliWaseem SajjadMuhammad ArshadMaqsood AliRahat Maqsoo...

João Carlos dos Santos Nazionalità Brasile Altezza 183[1] cm Peso 88[1] kg Calcio Ruolo Difensore Termine carriera 2006 Carriera Squadre di club1 1992-1993 Democrata-GV? (?)1994 Cruzeiro? (?)1995 Democrata-GV? (?)1996-1999 Cruzeiro13 (1)1999-2001 Corinthians26 (3)2001-2002 Cruzeiro17 (3)2002-2003 Cerezo Osaka53 (5)2004 Botafogo18 (1)2005 Paysandu11 (2)2006 Democrata-GV? (?)2006 Ipatinga? (?) Nazionale 1999 Brasile...

Town in New South Wales, AustraliaYulumaNew South WalesYuluma SiloYulumaLocation in New South WalesCoordinates35°09′55″S 146°29′31″E / 35.16528°S 146.49194°E / -35.16528; 146.49194Postcode(s)2645Elevation149 m (489 ft)Location 7 km (4 mi) from Boree Creek 29 km (18 mi) from Urana LGA(s)Federation CouncilCountyUranaState electorate(s)Wagga Wagga Yuluma is a rural community in the central part of the Riverina and a railway stati...
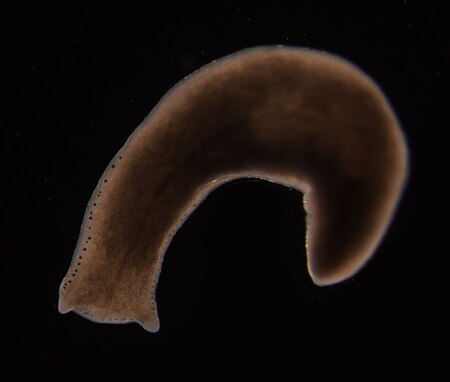
State in which the rate of mortality from senescence is stable or decreasing Not to be confused with immortalised cell line. Biological immortality (sometimes referred to as bio-indefinite mortality) is a state in which the rate of mortality from senescence is stable or decreasing, thus decoupling it from chronological age. Various unicellular and multicellular species, including some vertebrates, achieve this state either throughout their existence or after living long enough. A biologically...

Camp d'internement du Récébédou Présentation Type Camp de transit et d'internement Gestion Date de création février 1941 Date de fermeture septembre 1942 Victimes Géographie Pays France Région Midi-Pyrénées Localité Portet-sur-Garonne (Haute-Garonne) Coordonnées 43° 32′ 31″ nord, 1° 24′ 31″ est Géolocalisation sur la carte : France Camp d'internement du Récébédou modifier Le camp du Récébédou est un camp d'internement pour...

History United States NameUSS SC-255 Builder George Lawley & Sons Neponset, Massachusetts Commissioned19 November 1917 FateSold on 24 June 1921; Ultimate fate unknown General characteristics Class and typeSC-1-class submarine chaser Displacement75 t[1] Length110 ft (34 m)[1] Beam13 ft 6 in (4.11 m)[1] Draft6 ft 3 in (1.91 m)[1] Propulsion 3 × 660 hp (490 kW) Standard gasoline engines 3 shafts[1] Sp...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Conservatoire de musique du Québec à Trois-Rivières – news · newspapers · books · scholar · JSTOR (March 2010) Conservatoire de musique du Québec à Trois-RivièresConservatoire de Musique de Trois-Rivières, Quebec, CanadaAbbreviationCMQTFormatio...

Bupati Nagan Raya Republik IndonesiaLambang Bupati Nagan Raya Republik IndonesiaPetahanaFitriany Farhas (Pj)sejak 10 Oktober 2022KediamanPendapa Bupati Nagan Raya ( Komplek Perkantoran Suka Makmue )Masa jabatan5 tahun (definitif)Dibentuk2002 (UU No.4 TH 2002)Pejabat pertamaDrs. Teuku ZukarnainiSitus webSitus Resmi Kabupaten Nagan Raya Berikut ini adalah daftar Bupati Nagan Raya. No Bupati Mulai Jabatan Akhir Jabatan Wakil Bupati Keterangan Ref. Drs. H. Teuku Zukarnaini 2002 2006 Penjabat...

Celebrazione dell'Italian Heritage Parade (ex Columbus Day) a San Francisco nel 2011 Gli italiani di San Francisco sono una storica comunità di italoamericani residenti nell'area metropolitana di San Francisco. A differenza delle comunità della East coast, gli italiani di San Francisco sono in maggioranza originari dall'Italia settentrionale, centrale e dalle isole[1]. Secondo la National Italian American Foundation nel 2000 costituivano il 5% della popolazione cittadina. Storicamen...

Fictional character from the Family Guy franchise For other uses, see Brian Griffin (disambiguation). Brian the dog redirects here. For the real dog, see Bing (dog). Fictional character Brian GriffinFamily Guy characterFirst appearanceDeath Has a Shadow (1999)Created bySeth MacFarlaneDesigned bySeth MacFarlaneVoiced bySeth MacFarlaneIn-universe informationSpeciesDog (white labrador retriever)GenderMaleOccupationWriterFamilyPeter Griffin (owner/best friend)Lois Griffin (owner/friend)Meg Griffi...
Railroad station in Beacon, New York, US BeaconView south down the island platformGeneral informationLocation1 Ferry PlazaBeacon, New YorkCoordinates41°30′23″N 73°59′05″W / 41.5064°N 73.9848°W / 41.5064; -73.9848Owned byMetro-NorthLine(s)Hudson LinePlatforms1 island platform, 1 side platformTracks3Connections Dutchess County Public Transit Leprechaun Lines: Newburgh-Beacon-Stewart Shuttle NY Waterway: Newburgh–Beacon FerryConstructionParkingYesBicycle fac...

Government of Sudan from 1985 to 2019 Republic of the Sudanجمهورية السودان (Arabic)Jumhūrīyat as-Sūdān1985–2019 Flag Emblem Map of Sudan before South Sudanese independence on July 9, 2011CapitalKhartoum15°38′N 032°32′E / 15.633°N 32.533°E / 15.633; 32.533Largest cityOmdurmanOfficial languagesArabicEnglishEthnic groups 70% Sudanese Arabs[1]5.5% Beja2.5% Nuba2% Fur1.2% Egyptian[2]0.5% Fulani[3]18.34% otherReli...

Fell in the Lake District, Cumbria, England For the fell near Mardale in the Lake District, see Harter Fell (Mardale). Harter FellHarter Fell as seen from Wha House Farm in EskdaleHighest pointElevation653 m (2,142 ft)[1]Prominence276 m (906 ft)Parent peakScafell PikeListingMarilyn, Hewitt, Wainwright, NuttallCoordinates54°23′18″N 3°12′15″W / 54.38833°N 3.20417°W / 54.38833; -3.20417GeographyHarter FellLocation in the Lake D...

Device for suppressing part of a signal In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other ta...