Règle 68-95-99,7
|
Read other articles:

The Seasons Title page of 1805 editionAuthorJames ThomsonOriginal titleThe SeasonsCountryScotlandLanguageEnglishGenreBlank versePublication date1730 (1730)Media typePrintTextThe Seasons at Wikisource The Seasons is a series of four poems written by the Scottish author James Thomson. The first part, Winter, was published in 1726, and the completed poem cycle appeared in 1730.[1] The poem was extremely influential, and stimulated works by Joshua Reynolds, John Christophe...

2016 South Korean television series The K2Promotional posterGenreActionMelodramaPolitical thrillerCreated byJinnie ChoiStudio DragonWritten byJang Hyuk-rinDirected byKwak Jung-hwanSung Yong-ilStarringJi Chang-wookSong Yoon-ahIm Yoon-ahJo Sung-haKim Kap-sooComposerChoi Cheol-hoCountry of originSouth KoreaOriginal languageKoreanNo. of episodes16ProductionExecutive producerPark Ho-sikProducersKim Geun-hong Moon Boo-miProduction locationsSeoul, South KoreaBarcelona, SpainRunning time60 minsProduc...

Paul Arizin Paul Joseph Arizin (9 April 1928 – 12 Desember 2006) adalah seorang mantan pemain bola basket dari Amerika Serikat. Karier Ia bermain untuk Philadelphia Warriors dalam NBA. Ia pensiun sebelum tim ini pindah ke San Fransisco. Pranala luar (Inggris) Basketball Hall of Fame profile Diarsipkan 2006-09-06 di Wayback Machine. lbsTim Sepanjang Masa Peringatan 50 Tahun National Basketball Association Bill Russell Bill Sharman Bill Walton Billy Cunningham Bob Cousy Bob Pett...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Sumo – berita · surat kabar · buku · cendekiawan · JSTOR Sumo (相撲)Asashōryū dan KotoshōgikuFokusBergumulKekerasankontak badan penuhNegara asal JepangOlahraga olimpikTidakSitus resmihttp://www.sumo.or.j...

Radio station in Mobile, AlabamaWNTMMobile, AlabamaBroadcast areaMobile metropolitan areaFrequency710 kHzBrandingNewsRadio 710 WNTMProgrammingFormatNews/talkAffiliationsFox News RadioPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsWKSJ-FM, WMXC, WRGV, WRKH, WTKX-FMHistoryFirst air dateSeptember 26, 1946 (as WKRG)Former call signsWKRG (1946–1994)WNTM (1994–2004)WPMI (2004–2007)[1]Call sign meaningNews Talk of Mobile[2][3]Technical...

Untung SyamsuriUntung saat diadili di Jakarta pada tahun 1966 Informasi pribadiLahir(1926-07-03)3 Juli 1926Kebumen, Jawa Tengah, Hindia BelandaMeninggalSeptember 1967Cimahi, Jawa Barat, IndonesiaKarier militerPihak Kekaisaran Jepang (1943—1945) Indonesia (1945—1965)Dinas/cabang PETA (1943—1945) TNI Angkatan Darat (1945—1965)Masa dinas1943—1965Pangkat Letnan KolonelKomandoResimen TjakrabirawaPertempuran/perangRevolusi Nasional IndonesiaGerakan 30 SeptemberSunting kotak...

American politician This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this template message) John C. McKenzieMember of the U.S. House of Representativesfrom Illinois's 13th districtIn officeMarch 4, 1911 – March 4, 1925Preceded byFrank O. LowdenSucceeded byWilliam R. Johnson Personal detailsBorn(1...

مارلين مونرو وتوم إيويل في فيلم سنة الحكة السابعة (1955). الكوميديا الرومانسية (بالإنجليزية: Romantic comedy) (يُطلق عليها كلفظ منحوت: روميديا (بالإنجليزية: romedy))، هي نوع من أنواع محاور الحبكات الفكاهية التي تركز على الأفكار الرومانسية، مثل مدى قدرة الحب الحقيقي على التغلب على معظ�...

Агентство національної безпеки (АНБ)англ. National Security Agency (NSA) Штаб-квартира АНБ Загальна інформація: Тип: спецслужба Юрисдикція: США Дата заснування: 4 листопада 1952 Відомство-попередник: Агентство безпеки збройних сил Девіз: Defending Our Nation. Securing The Future.(укр. Захищаючи ...

جزء من الإبادة الجماعية للسكان الأصليينالإبادة الجماعية للسكان الأصليين مشاكل إبادة بيئية تطهير عرقي علم اجتماع العلاقات الإثنية والعرقية Forced assimilation / تحول قسري Genocide Denial اغتصاب إبادي استعمار استيطاني أفريقيا جنوب الصحراء الكبرى الفظائع في دولة الكونغو الحرة الإبادة �...

Chaudhry Mohammad Ali Nama dalam bahasa asli(ur) چوہدری محمد علی BiografiKelahiran15 Juli 1905 Jalandhar (Raj Britania Raya) Kematian2 Desember 1982 (77 tahun)Defence Housing Authority, Karachi Daftar Perdana Menteri Pakistan 12 Agustus 1955 – 12 September 1956 ← Muhammad Ali Bogra – Huseyn Shaheed Suhrawardy → Defence Minister of Pakistan 12 Agustus 1955 – 12 September 1956 ← Muhammad Ayub Khan – Huseyn Shaheed Suhrawardy &...

Borough in Ocean County, New Jersey, US Borough in New JerseyIsland Heights, New JerseyBorough SealLocation of Island Heights in Ocean County highlighted in red (right). Inset map: Location of Ocean County in New Jersey highlighted in orange (left).Census Bureau map of Island Heights, New JerseyIsland HeightsLocation in Ocean CountyShow map of Ocean County, New JerseyIsland HeightsLocation in New JerseyShow map of New JerseyIsland HeightsLocation in the United StatesShow map of the United Sta...

كأس العالم للسيدات تحت 17 سنة 2016كأس العالم للسيدات تحت 17 سنة الأردن 2016شعار البطولةتفاصيل المسابقةالبلد المضيف الأردنالتواريخ30 سبتمبر - 21 أكتوبرالفرق16الأماكن4 ملاعب (في 3 مدن مضيفة)المراكز النهائيةالبطل كوريا الشماليةالوصيف اليابانالمركز الثالث إسبانياالمر�...

Chemical compound PirlindoleClinical dataTrade namesPirazidolRoutes ofadministrationOralATC codenoneLegal statusLegal status In general: ℞ (Prescription only) Pharmacokinetic dataBioavailability20–30%Protein binding95%MetabolismhepaticOnset of action2 to 8 hoursElimination half-lifeup to 8 days [1]Excretionurine (50–70%), feces (25–45%)Identifiers IUPAC name 8-methyl-2,3,3a,4,5,6-hexahydro-1H-pyrazino[3,2,1-jk]carbazole CAS Number60762-57-4PubChem CID68802IUPHAR/BPS6...

Swiss cyclist (born 1966) Rolf JärmannPersonal informationFull nameRolf JärmannBorn (1966-01-31) 31 January 1966 (age 58)Arbon, SwitzerlandHeight1.82 m (6 ft 0 in)Weight73 kg (161 lb; 11 st 7 lb)Team informationCurrent teamRetiredDisciplineRoadRoleRiderMajor winsAmstel Gold Race (1993, 1998) Rolf Järmann (born 31 January 1966 in Arbon) is a retired road bicycle racer from Switzerland, who was a professional rider from 1988 to 1999. He twice...

Greek footballer (1926–2000) Andreas Mouratis Personal informationDate of birth (1926-11-29)29 November 1926Place of birth Piraeus, GreeceDate of death 10 December 2000(2000-12-10) (aged 74)Place of death Piraeus, GreecePosition(s) DefenderYouth career1936–1943 A.E. ChromatourgionSenior career*Years Team Apps (Gls)1943–1945 Proodeftiki 1945–1955 Olympiacos 1955–1961 Argonaftis Piraeus International career1948–1953 Greece 16 (1)1952 Greece Olympic 0 (0)1962 Greece Military *C...

25°01′56″N 102°42′25″E / 25.03210°N 102.70695°E / 25.03210; 102.70695 惠光寺塔和常乐寺塔惠光寺塔(西寺塔)、常乐寺塔(东寺塔)全国重点文物保护单位中华人民共和国国务院公布地址云南省昆明市分类古建筑时代唐、清编号6-739认定时间2006年 东西寺塔是位于云南省昆明市的两座古代佛塔,原分别坐落于常乐寺和惠光寺内,故又名常乐寺塔和惠光寺塔[1]�...
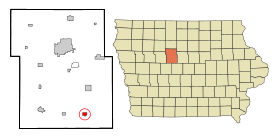
لمعانٍ أخرى، طالع دايتون (توضيح). دايتون الإحداثيات 42°15′46″N 94°04′09″W / 42.262777777778°N 94.069166666667°W / 42.262777777778; -94.069166666667 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ويبستر خصائص جغرافية المساحة 2.191789 كيلومتر مربع2.1917...

Pour le club omnisport, voir SC Rotor Volgograd. Rotor Volgograd Généralités Nom complet Футбольный клуб «Ротор» Волгоград(Futbolny klub «Rotor» Volgograd) Noms précédents Traktorostroïtel (1929-1935)Dzerjinets-STZ (1936)Traktor (1937-1947)Torpedo (1948-1957)Traktor (1958-1969)Stal (1970-1971)Barrikady (1972-1974) Fondation 1929[n 1] Statut professionnel 1936-20152016- Couleurs Bleu et bleu ciel Stade Volgograd Arena (45 000 places) Siège Volg...

Smith's Bible Dictionary 1863 Easton's Bible Dictionary 1894 Nave's Topical Bible 1905 Names play a variety of roles in the Bible. They sometimes relate to the nominee's role in a biblical narrative, as in the case of Nabal, a foolish man whose name means fool.[1] Names in the Bible can represent human hopes, divine revelations, or are used to illustrate prophecies.[2][clarification needed] The titles given to characters, locations, and entities in the Bible can diffe...





