Graphe (mathématiques discrètes)
|
Read other articles:

Toivo Korpela (stående). Korpelarörelsen var en religiös väckelserörelse i Tornedalen under 1930-talet. Den grundades av Toivo Korpela. Rörelsen grundas Bönemöte hos Korpelarörelsen. I slutet av 1920-talet kom den finländske jordbrukaren Toivo Korpela till Tornedalen. Han hade vuxit upp i ett starkt religiöst hem i Etseri. Korpela, som var aktiv inom östlæstadianismen, började under sin värnpliktstid predika vid rörelsens väckelsemöten. Han lockade snabbt många mötesdeltag...

British politician For the rugby league footballer of the 1910s for England, and Dewsbury, see Thomas Milner. For other people named Thomas Gibson, see Thomas Gibson (disambiguation). The Right HonourableThomas Milner GibsonPresident of the Board of TradeIn office6 July 1859 – 26 June 1866MonarchVictoriaPrime MinisterThe Viscount Palmerston The Earl RussellPreceded byThe Earl of DonoughmoreSucceeded bySir Stafford Northcote, BtVice-President of the Board of TradeIn office8 July 184...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Blues at Sunset – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) 1993 live album by Albert KingBlues at SunsetLive album by Albert KingReleased1993RecordedAugust 20, 1972 (Wattstax) and July 1...

присілок Данильцево Данильцево Країна Росія Суб'єкт Російської Федерації Владимирська область Муніципальний район Судогодський район Поселення Муромцевське сільське поселення Код ЗКАТУ: 17252000046 Код ЗКТМО: 17652434141 Основні дані Населення ▼ 10 (2010)[1] Поштовий індекс ...

Kamp konsentrasi Stutthof dimana sejumlah kecil sabun diyakini dibuat dari jasad-jasad korban manusia. Pada abad ke-20, terdapat berbagai tuduhan soal sabun yang terbuat dari lemak tubuh manusia. Pada Perang Dunia I, pers Inggris mengklaim bahwa Jerman memiliki pabrik jasad dimana mereka memakai jasad-jasad prajurit mereka sendiri untuk membuat gliserin dan sabun. Pada Perang Dunia II, sabun diyakini diproduksi massal dari jasad-jasad korban kamp konsentrasi Nazi yang terletak di Polandia yan...

Sultanate in Sumatra For other uses, see Serdang (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sultanate of Serdang – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this template message) Sultanate of Serdangﻛﺴﻠطﺎﻧﻦ سردڠ1723–1946 ...

塩分濃度差発電(えんぶんのうどさはつでん)は、塩水と淡水間に生じる浸透圧や蒸気圧力の差を電力に変換する発電方式である。 河川の水を上流に240m押し上げるほどのエネルギーをも発生させると言われる。 関連項目 ウィキメディア・コモンズには、塩分濃度差発電に関連するカテゴリがあります。 海水 汽水 外部リンク 竹内敬治 (2009年4月26日). “海水と淡水

Ein Adler-Super-Trumpf-Rennwagen, der 1937 und 1938 in Le Mans an den Start ging. Petar Josef Georg Levin Graf Orssich von Slavetich (meist kurz Petar Graf Orssich oder Peter Graf Orssich; * 4. Mai 1907 in Wien; † 3. Juli 1961 in Saint-Dizier, Frankreich) war ein österreichischer (nach einigen Quellen auch deutscher) Adeliger und Automobilrennfahrer. Inhaltsverzeichnis 1 Werdegang 2 Statistik 2.1 Le-Mans-Ergebnisse 3 Weblinks 4 Einzelnachweise Werdegang Petar Graf Orssich war der Sohn von ...

U.S. psychology professor and language analyst James Whiting PennebakerJames W. Pennebaker at the 2011 Texas Book Festival.Born (1950-03-02) March 2, 1950 (age 73)Midland, Texas, U.S.NationalityAmericanOccupationRegents Centennial Professor of Psychology at the University of Texas at AustinKnown forSocial psychologyWriting therapyAnthropological linguisticsPsycholinguisticsSociolinguisticsphysical symptoms James Whiting Pennebaker (born March 2, 1950) is an American social psycholog...

2005 video gameRadiata StoriesNorth American box artDeveloper(s)tri-AcePublisher(s)Square EnixDirector(s)Naoki AkiyamaProducer(s)Yoshinori YamagishiProgrammer(s)Yoshiharu GotandaArtist(s)Takashi JoonoHiroshi KonishiWriter(s)Masatoshi MidoriComposer(s)Noriyuki IwadarePlatform(s)PlayStation 2ReleaseJP: January 27, 2005NA: September 6, 2005Genre(s)Action role-playingMode(s)Single-playing Radiata Stories[a] is an action role-playing video game. It was developed by tri-Ace and published by...

Place in SingaporeRaffles PlaceName transcription(s) • Chinese莱佛士坊 • PinyinLáifóshì Fāng • MalayPesara Raffles • Tamilராஃபிள்ஸ் பிளேஸ்Raffles PlaceLocation of Raffles Place within SingaporeCoordinates: 1°17′03.94″N 103°51′04″E / 1.2844278°N 103.85111°E / 1.2844278; 103.85111 1°17′02″N 103°51′05″E / 1.28389°N 103.85139°E / 1.2838...

Species of mammal Golden-backed tree rat Conservation status Near Threatened (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Rodentia Family: Muridae Genus: Mesembriomys Species: M. macrurus Binomial name Mesembriomys macrurus(Peters, 1876) The golden-backed tree rat (Mesembriomys macrurus) is a species of rodent in the family Muridae, found only in Australia. It is present in the Charnley River–Artesian R...

151st Aviation Regimentcoat of armsCountryUnited States of AmericaBranchUnited States Army Aviation BranchTypeAviationPart ofSouth Carolina Army National GuardAircraft flownAttack helicopterAH-64E ApacheUtility helicopterUH-72A LakotaMilitary unit The 151st Aviation Regiment is an aviation regiment of the U.S. Army, primarily provided by the South Carolina Army National Guard. Structure 1st Battalion (Attack Reconnaissance) Ghostriders at McEntire Joint National Guard Base, Eastover Comp...

Figure in Greek mythology For other uses, see Sarpedon.Sarpedon IKing of LyciaMember of the Cretan Royal FamilyHypnos and Thanatos carrying the body of Sarpedon from the battlefield of Troy; detail from an Attic white-ground lekythos, ca. 440 BC.SuccessorEvanderAbodeCrete, later LyciaPersonal informationParentsZeus and EuropaSiblingsMinos and RhadamanthusConsort(1) Miletus (lover)(2) ?Offspring(2) Evander In Greek mythology, Sarpedon (/sɑːrˈpiːdən/ or /sɑːrˈpiːdɒn/; Ancient Gre...

نيوكاسل أندر لايمالبلد المملكة المتحدة المنطقة ميدلاند الغربية المساحة 81٫083 كم²[1] الدائرة الانتخابيةتأسست في 24 نوفمبر 1885 عدد المقاعد 1 مجلس العموم أنشئ من Newcastle-under-Lyme (en) تعديل - تعديل مصدري - تعديل ويكي بيانات 53°02′N 2°18′W / 53.04°N 2.30°W / 53.04; -2.30 نيوكاسل أندر �...

Dutch footballer and manager Joop Brand Brand in 1978Personal informationDate of birth (1936-06-11) 11 June 1936 (age 87)Place of birth Dubbeldam, NetherlandsPosition(s) DefenderSenior career*Years Team Apps (Gls)1947–1955 Xerxes 1955–1957 DFC 1957–1960 HVC 1960–1961 DFC 1961–1964 Heracles Managerial career1969–1971 DWS1971–1973 Haarlem1973–1976 AZ1978–1980 Go Ahead Eagles1980 Sparta1980–1983 Telstar1985–1986 AZ1996 FC VVV *Club domestic league appearances and goals...

1976 occupation of abortion clinic Rooie Vrouwen in de PvdA (Red Women in the PvdA) was the name of a woman's organization active in the Dutch Labour Party, the PvdA. The organization started as a union of women's organizations, called union of social-democrat women's clubs[1] at the time of the Social Democratic Workers' Party (Netherlands), one of the predecessors of the PvdA.[2] The organization's goal was to emancipate the masses of proletarian women. It owned a building n...

Nikos Zīsīs Nikos Zīsīs con l'uniforme della Grecia nel 2008 Nazionalità Grecia Altezza 196 cm Peso 94 kg Pallacanestro Ruolo Playmaker / guardia Termine carriera 28 giugno 2021 Carriera Giovanili 1996-2000 ΧΑΝΘ Salonicco Squadre di club 2000-2005 AEK Atene115 (866)2005-2007 Pall. Treviso54 (550)2007-2009 CSKA Mosca39 (298)2009-2012 Mens Sana Siena86 (614)2012-2013 Bilbao Berri34 (306)2013-2014 UNICS Kazan'16 (137)2014-2015 Fenerbahçe Ü...

Description of the Ableman Gorge Ableman's Gorge State Natural AreaIUCN category V (protected landscape/seascape)Ableman's Gorge in 2009Location in WisconsinShow map of WisconsinLocation in United StatesShow map of the United StatesLocationSauk County, WisconsinNearest cityRock Springs, WisconsinCoordinates43°29′18″N 89°55′17″W / 43.48833°N 89.92139°W / 43.48833; -89.92139Area127 acres (51 ha)Established1969Governing bodyWisconsin Department ...

Swedish extreme metal band DissectionDissection live in 2005 (vocalist and guitarist Jon Nödtveidt at front)Background informationOriginStrömstad, SwedenGenres Melodic black-death[1][2] black metal[3][1] melodic death metal[4] blackened death metal[5] Years active1989–19972004–2006LabelsNo FashionNuclear BlastThe EndPast members Jon Nödtveidt Set Teitan Tomas Asklund Mattias Mäbe Johansson John Zwetsloot Johan Norman Peter Palmdahl Emil ...





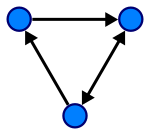





![{\displaystyle [v_{i},v_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e191d44e300edb46fc9b9a1fbc9ca6f3e9da40)

![{\displaystyle [v_{n},v_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a167d15d324cfa222111e35bd2fe5d7576e41f)

