Degré d'une application
|
Read other articles:
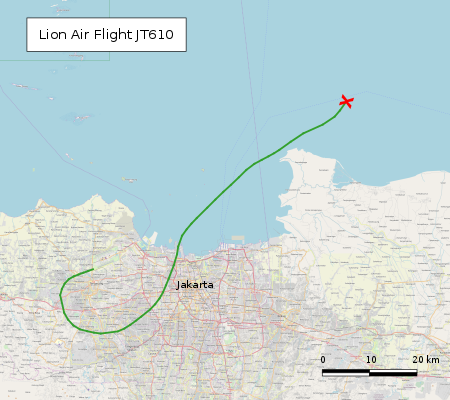
2018 aircraft crash in the Java Sea, Indonesia, killing 189 See also: Boeing 737 MAX groundings Lion Air Flight 610PK-LQP, the aircraft involved in the accidentAccidentDate29 October 2018 (2018-10-29)SummaryLoss of control due to runaway trim from MCAS activation, inadequate maintenanceSiteJava Sea, off the north coast of Karawang Regency, Indonesia 5°46′15″S 107°07′16″E / 5.77083°S 107.12111°E / -5.77083; 107.12111AircraftAircraft typeB...
Hohenlinden. Hohenlinden adalah kota yang terletak di distrik Ebersberg di Bayern, Jerman. Kota Hohenlinden memiliki luas sebesar 17.32 km² . Hohenlinden pada tahun 2006, memiliki penduduk sebanyak 2.751 jiwa. lbsKota dan kotamadya di EbersbergAnzing | Aßling | Baiern | Bruck | Ebersberg | Egmating | Emmering | Forstinning | Frauenneuharting | Glonn | Grafing bei München | Hohenlinden | Kirchseeon | Markt Schwaben |...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) مقارنة بين حجم أكبر أربع طائرات الأنتونوف إيه إن-225(الأخضر)، والإتش-4 هيركوليز (ذهبى)، بوينغ 747-8 (أزرق)، والإي�...

Celtic subfamily including Welsh, Cornish, Breton and Cumbric For the individual language ancestral to the Brittonic languages, see Common Brittonic. Brittonic*Brittonikā, Brythonic, British CelticGeographicdistributionWales, Cornwall, Brittany, in antiquity all of Great Britain and the Isle of Man, during the Early Middle Ages in Northern England and Southern Scotland and other western parts of Britain, Pictland, GaliciaLinguistic classificationIndo-EuropeanCelticInsular CelticBrittonicProt...

Brad Friedel Informasi pribadiNama lengkap Bradley Howard FriedelTanggal lahir 18 Mei 1971 (umur 52)Tempat lahir Lakewood, Ohio, United StatesTinggi 6 ft 3 in (1,91 m)Posisi bermain Penjaga gawangKarier junior1990–1992 UCLAKarier senior*Tahun Tim Tampil (Gol)1994–1995 USSF 0 (0)1994 → Newcastle United (loan) 0 (0)1995 → Brøndby (pinjaman) 0 (0)1995–1996 Galatasaray 30 (0)1996–1997 Columbus Crew 38 (0)1997–2000 Liverpool 25 (0)2000–2008 Blackburn Rovers 28...

Football league seasonTorneo DescentralizadoWinning squadSeason1973Dates15 April 1973 –13 January 1974ChampionsDefensor Lima1st titleRelegatedSportivo HuracánAtlético TorinoJosé GálvezDeportivo SIMACopa LibertadoresDefensor LimaSporting CristalCopa Simón BolívarDefensor LimaTop goalscorerFrancisco Gonzalez (25 goals)[1]← 1972 1974 → The 1973 Torneo Descentralizado was the 57th season of the Peruvian Primera División and the ninth season of the Torneo Descentralizado. It w...

Commune in Grand Est, FranceSouain-Perthes-lès-HurlusCommuneThe town hall in SouainLocation of Souain-Perthes-lès-Hurlus Souain-Perthes-lès-HurlusShow map of FranceSouain-Perthes-lès-HurlusShow map of Grand EstCoordinates: 49°11′04″N 4°32′39″E / 49.1844°N 4.5442°E / 49.1844; 4.5442CountryFranceRegionGrand EstDepartmentMarneArrondissementChâlons-en-ChampagneCantonArgonne Suippe et VesleIntercommunalityRégion de SuippesGovernment • Mayor (2...

Barking Power StationBarking Reach Power StationViewed from the south in October 2007CountryEnglandLocationGreater LondonCoordinates51°31′16″N 0°08′49″E / 51.5210°N 0.1470°E / 51.5210; 0.1470StatusDecommissioned and demolishedConstruction began'A' 1925-28; 'B' 1931-39; 'C' 1952-54; Barking Reach 1992-95Commission date'A' 1925; 'B' 1933; 'C' 1954; Barking Reach 1995Decommission date'A' 1969; 'B' 1976; 'C' 1981; Barking Reach 2018Owner(s)As op...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Moylagh, County Tyrone – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this message) Drumconnelly Road traversing Moylagh townland Moylagh (from Irish Maolach)[1] is a townland near Gortaclare in County Tyrone, N...

Football derby between Real Sociedad and Athletic Bilbao Not to be confused with Basque basketball derby. Basque derbyLocationBasque Country, SpainTeamsAthletic BilbaoReal SociedadFirst meeting4 April 1909Copa del ReyClub Ciclista 4–2 Athletic BilbaoLatest meeting13 January 2024La LigaAthletic Bilbao 2–1 Real SociedadStadiumsSan Mamés (Bilbao)Anoeta (San Sebastian)StatisticsMeetings total191Most winsAthletic Bilbao (79)Top scorerTelmo ZarraJesús María Satrústegui(14 each)Largest victo...

Franklin PangbornCuplikan dari trailer untukTopper Takes a Trip, 1939Lahir(1889-01-23)23 Januari 1889Newark, New Jersey, Amerika SerikatMeninggal20 Juli 1958(1958-07-20) (umur 69)Laguna Beach, California, Amerika SerikatPekerjaanPemeranTahun aktif1910–1958 Franklin Pangborn (23 Januari 1889 – 20 Juli 1958) adalah seorang pemeran karakter komedi Amerika Serikat yang dikenal karena memerankan peran-peran kecil namun terkenang dengan sifat komika. Ia tampil dalam ban...

STS-117Emblema missione Dati della missioneOperatoreNASA NSSDC ID2007-024A SCN31600 ShuttleAtlantis VettoreSpace Shuttle Lancio8 giugno 2007, 7:38 p.m. EDT (23:38 UTC) Luogo lancioRampa 39A Atterraggio22 giugno 2007, 3:49 p.m. EDT (19:49 UTC) Sito atterraggioEdwards Air Force Base (pista 22) (34°54′20″N 117°53′01″W / 34.905556°N 117.883611°W34.905556; -117.883611) Durata13 giorni, 20 ore, 12 minuti e 44 secondi Proprietà del veicolo spazialePeso al lancio122 ...

Village in Kerman province, Iran For other places with the same name, see Ezzatabad. Village in Kerman, IranEzzatabad Persian: عزتابادVillageEzzatabadCoordinates: 29°22′32″N 55°47′04″E / 29.37556°N 55.78444°E / 29.37556; 55.78444[1]CountryIranProvinceKermanCountySirjanDistrictCentralRural DistrictNajafabadPopulation (2016)[2] • Total2,085Time zoneUTC+3:30 (IRST) Ezzatabad (Persian: عزتاباد)[a] is a vill...

Battle in the 2022 Russian invasion of Ukraine For other military conflicts involving Odesa, see Battle of Odesa. Odesa strikesPart of the Russian invasion of UkraineAftermath of a Russian missile strike against warehouses in Odesa on 24 FebruaryDate24 February 2022 (2022-02-24) – present(2 years, 2 months, 3 weeks and 1 day)LocationOdesa, Odesa Oblast, UkraineBelligerents Russia UkraineUnits involved Russian Armed Forces Russian Air...

2007 EP by Fight Like ApesHow Am I Supposed to Kill You If You Have All the Guns?EP by Fight Like ApesReleasedMay 2007GenreAlternative rock,[1] karate rock,[2][3] punk rock[4]LabelFIFA RecordsFight Like Apes chronology How Am I Supposed to Kill You If You Have All the Guns?(2007) David Carradine is a Bounty Hunter Whos Robotic Arm Hates Your Crotch(2007) How Am I Supposed to Kill You If You Have All the Guns? is the debut four-track EP of Fight Like Ape...
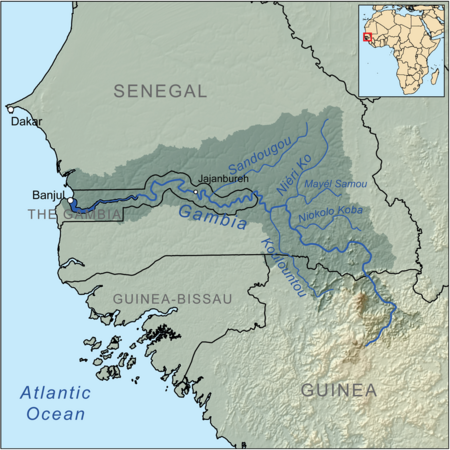
Major river in West Africa Gambia RiverGambia River in the Niokolo-Koba National ParkMap of the Gambia River drainage basinLocationCountriesGuineaSenegalThe GambiaPhysical characteristicsSourceFouta Djallon • location Labé, Guinea • coordinates11°24′43″N 12°13′34″W / 11.412°N 12.226°W / 11.412; -12.226 • elevation795 m (2,608 ft) MouthAtlantic Ocean • locationBanjul, The Gambia&...

Xavier DorXavier pada tahun 2019Lahir30 Januari 1929Marseille, PrancisMeninggal4 April 2020(2020-04-04) (umur 91)Paris, PrancisKebangsaan PrancisPekerjaanAhli embriologi Xavier Dor (30 Januari 1929 – 4 April 2020) merupakan ahli embriologi asal Prancis yang tersohor akan keaktifannya dalam menentang praktik aborsi.[1] Kehidupan pribadi Xavier merupakan anak dari keluarga Katolik. Ayahnya merupakan direktur Compagnie Générale Transatlantique. Xavier memilik...

Experimental Japanese shinkansen trainset Class 952/953 STAR21Class 952Class 953In service1992–1998ManufacturerHitachi, Kawasaki Heavy Industries, Nippon SharyoConstructed1992Scrapped1998Number built9 vehiclesNumber in serviceNoneNumber preserved3 vehiclesNumber scrapped6 vehiclesFormation9 carsFleet numbersS5OperatorsJR EastLines servedTohoku Shinkansen, Joetsu ShinkansenSpecificationsCar body constructionAluminium alloyWidth3,100 mm (10 ft 2 in)Maximum speed350 km/...

لمعانٍ أخرى، طالع الأحد الدامي (توضيح). الأحد الدامي 1887. يصور هذا الرسم من أخبار لندن المصورة شرطيّاً يضربه أحد المتظاهرين وهو يرفع لافتة من إحدى المتظاهرات وقع يوم الأحد الدامي في لندن في 13 نوفمبر 1887، عندما اشتبك المتظاهرون الذين احتجوا على البطالة والإكراه في أيرلن...

Multi-purpose sports arena in Quezon City, Philippines Araneta ColiseumThe Big DomeAraneta Coliseum in 2017Full nameSmart Araneta ColiseumFormer namesAraneta Coliseum Cinema, Philippine Coliseum, and Shell ColiseumLocationAraneta City, Cubao, Quezon City, Metro ManilaCoordinates14°37′14″N 121°3′12″E / 14.62056°N 121.05333°E / 14.62056; 121.05333Public transit Araneta Center-Cubao 3 Araneta Center-Cubao 51 53 61 Farmers Plaz...













