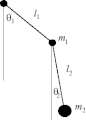
Coordonnées généralisées
|
Read other articles:

Inukranyanoукраї́нська мо́ваPaglitok[ʊkrɐˈjinʲsʲkɐ ˈmɔwɐ]Namulong lumad saUkranyaBungto/DapitTunga ug Kadaspang UropaKaliwatKatawhang UkranyanoMga lumadnongmamumulong40 ka milyon (2000)[1]Tigpagsulti: anaa sa 45 ka milyon (sumada)[2]KabánayIndo-Urupanhon Balto-SlavicEslaboSidlakang EslaboInukranyanoSayo nga gihulag:Pruto-Indo-Urupanhon Pruto-Balto-EslaboPruto-EslaboKaraang Sidlakang EslaboRutenyoInukranyano Sistema sa pagsulatSiriliko (Alphabetong Ukr...

Pesawat kargo militer besar, Lockheed C-5 Galaxy. Pengangkutan udara adalah suatu pengiriman persediaan atau personel terutama melalui pesawat angkut militer yang diatur secara teroganisir. Pengangkutan udara terdiri dari dua jenis: strategis dan taktis. Biasanya, pengangkutan udara strategis melibatkan pemindahan barang-barang jarak jauh (seperti melintasi atau keluar benua atau teater peperangan), sedangkan pengangkutan udara taktis berfokus pada pengerahan sumber daya dan material ke lokas...

Prison PlaybookPoster promosiHangul슬기로운 감빵생활 GenreKomedi hitam[1]PembuatLee Woo-jung[1]Ditulis olehJung Bo-hoonSutradaraShin Won-hoPemeranPark Hae-sooJung Kyung-hoNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduser eksekutifPark Sung-jaeProduserPark Soo-wooPengaturan kameraSingle-cameraDurasi90 menitRumah produksitvNDistributorCJ ENM NetflixRilis asliFormat gambar1080i (HDTV)Format audioDolby DigitalRilis22 November 2017 (2017-11-22)&#...

American animated TV series or program Danny PhantomGenre Action Adventure Comedy horror Fantasy Comic science fiction[1] Superhero Created byButch HartmanDeveloped bySteve MarmelVoices of David Kaufman Grey DeLisle Rickey D'Shon Collins Colleen O'Shaughnessey Rob Paulsen Kath Soucie Martin Mull Theme music composer Guy Moon Butch Hartman Opening themeDanny Phantom, performed by Deric Battiste and Guy MoonEnding themeDanny Phantom (instrumental)ComposerGuy MoonCountry of originUnited ...

State park in Delaware, United States Wilmington State ParksBrandywine Creek in Brandywine Park near downtown Wilmington looking downstream.Location of the Wilmington State Parks in DelawareLocationNew Castle, Delaware, United StatesCoordinates39°45′18″N 75°33′0″W / 39.75500°N 75.55000°W / 39.75500; -75.55000Elevation100 ft (30 m)Established1998Named forWilmington, DelawareGoverning bodyDelaware Department of Natural Resources and Environment...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Accelerator-based neutron source in Oak Ridge, Tennessee, USA This article is about the ORNL Spallation Neutron Source, in the US. For other spallation neutron sources, see Spallation § Spallation facilities. A DOE Office of Science User FacilityLocation:Oak Ridge National Laboratory, Oak Ridge, Tennessee, United StatesScientific Purpose:Provide unique information about the structure and properties of materials across the spectrum of biology, chemistry, physics, and engineering.Organiza...

A list of films produced in the decade of the 1930s. There are only two movies were released in this decade. The first Assamese picture, Joymati (1935) Rupkonwar Jyotiprasad Agarwala produced the first Assamese Film Joymati in 1935,[1][2][3] under the banner of Chitralekha Movietone. The second picture Indramalati was filmed between 1937 and 1938 finally released in 1939. A-Z film Year Release date Title[4] Director Cast Genre 1935 10 March 1935 Joymoti Jyotip...

Condado de Peñarrubias Corona condalPrimer titular Gaspar Ramírez de Arellano y PantojaConcesión Carlos II8 de noviembre de 1684Actual titular José María Gasset y Ramírez de Haro[editar datos en Wikidata] El condado de Peñarrubias es un título nobiliario español creado el 8 de noviembre de 1684 por el rey Carlos II a favor de Gaspar Ramírez de Arellano y Pantoja, general del ejército de Cataluña, maestre de campo y caballero de la Orden de Alcántara.[1] La denomi...
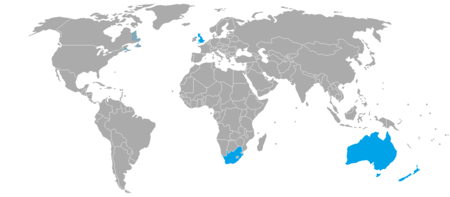
Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Cari berdasarkan nilai Glottolog Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman rumpun acak Rumpun bahasaBANZSLPersebaranPulau Britania Raya, Irlandia Utara, Afrika Selatan, Newfoundland dan Labrador, Maritimes, Australia, dan Selandia BaruPenggolongan bahasaSalah satu rumpun bahasa isyarat duniaBANZSL Isyarat Britania Isyarat Australia Isyarat Selandia Baru Isyarat Afrika Selatan Isyarat Mari...

German diplomat and member of Adolf Hitler's inner circle Walther HewelHewel in 1941Permanent Representative of the Reichsminister for Foreign Affairs to the FührerIn officeSeptember 1940 – 30 April 1945MinisterJoachim von RibbentropPreceded byPosition createdSucceeded byPosition abolishedHead of the Personal Staff of the Reichsminister for Foreign AffairsIn officeJune 1938 – 2 May 1945MinisterJoachim von RibbentropPreceded byPosition createdSucceeded byPosition abolish...

Національні символи Ізраїлю — символи що використовуються в Ізраїлі і закордоном представляють країну та її людей. Зміст 1 Національний прапор — прапор Ізраїлю 2 Національний герб — Герб Ізраїлю 3 Національний гімн — «Хатіква» 4 Національні кольори — сині...

У статті наведено матеріали стосовно тимчасово невстановлених осіб, що загинули під час російсько-української війни. Див. також: Втрати силових структур внаслідок російського вторгнення в Україну Зміст 1 Законодавча норма 2 Звіти 3 Поховання тимчасово невстановлених ві�...

German writer (1871–1950) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Heinrich Mann – news · newspapers · books · scholar · JSTOR (July 2010) (Learn how and when to remove this message) Heinrich MannHeinrich Mann in his Munich years (1894–1899)BornLuiz Heinrich Mann(1871-03-27)March 27, 1871Free City...

Book by theologian Alister McGrath The Dawkins Delusion? AuthorsAlister McGrathJoanna Collicutt McGrathLanguageEnglishSubjectReligionPublisherSociety for Promoting Christian KnowledgePublication date15 February 2007Publication placeUnited KingdomMedia typePrintPages75ISBN978-0-281-05927-0 The Dawkins Delusion? Atheist Fundamentalism and the Denial of the Divine is a book by the theologian Alister McGrath and the psychologist Joanna Collicutt McGrath. It is written from a Christian perspe...

Church of a singular female goddess Church of AphroditeGleb Botkin used this symbol of Aphrodite on the vestments for his Church of Aphrodite.Formationc. 1939TypeReligious organizationPurposestructural Monotheistic Church, based on a singular female goddess, who is named after Aphrodite, the ancient Greek love goddess.HeadquartersCharlottesville, Virginia, USLocation United States The Church of Aphrodite was a religious group founded in 1939 by Gleb Botkin, a Russian émigré to th...

14th Parliament of CanadaMajority parliament8 March 1922 – 5 September 1925Parliament leadersPrimeMinisterWilliam Lyon Mackenzie King29 December 1921 – 28 June 1926Cabinet12th Canadian MinistryLeader of theOppositionArthur Meighen29 December 1921 – 28 June 1926Party caucusesGovernmentLiberal PartyOppositionConservative Party*CrossbenchProgressive Party*LabourUnited Farmers* Arthur Meighen's Conservatives formed the Official Opposition although the Progressive Party had more se...

جامع العسافي في شارع الضباط راغبة خاتون تعتبر منطقة راغبة خاتون من المناطق العريقة في بغداد، وسميت نسبة إلى السيدة راغبة التي كانت ذات نفوذ كبير وتملك الأراضي في المنطقة. ومنطقة راغبة خاتون هي جزء من قضاء الأعظمية، وتضم أجزاء من حي الشماسية وحي المغرب، وفيها العديد من المس...

Belgian association football club This article is about the men's football team. For the women's team, see Standard Liège (women). Football clubStandard LiègeFull nameRoyal Standard de LiègeNickname(s)Les Rouches (The Reds)Founded1898; 126 years ago (1898)GroundStade Maurice DufrasneCapacity27,670[1]Head coachIvan LekoLeagueBelgian Pro League2023–24Belgian Pro League, 12th of 16WebsiteClub website Home colours Away colours Third colours Current season Royal Stan...

Devuansistema operativoLogoSviluppatoreVeteran Unix Admins FamigliaUnix-like Release iniziale1.0.0 (Jessie) (25 maggio 2017) Release corrente5.0.0 (Daedalus) (14 agosto 2023) Tipo di kernelMonolitico (Linux) Piattaforme supportateppc64el, i386, amd64, armel, armhf, arm64 Gestore dei pacchettiAPT (dpkg) Interfacce grafichePredefinito: Xfce Alternativi: MATE, KDE, LXQt, LXDE e Cinnamon Altri: disponibili dopo l'installazione (es. GNOME) Spazio utenteGNU LicenzaGNU General Public License Sta...














![{\displaystyle \theta _{1},\theta _{2}\in [0;2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f565d08faaf79f949f2298d7c9ada1c51dafeadc)