Distancia
|
Read other articles:
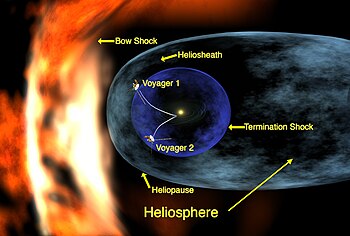
Letak Voyager 1 dan 2 (2005). Heliosheath (bahasa Indonesia: selubung surya) adalah zona antara gelombang kejut (termination shock) dan heliopause di perbatasan luar tata surya. Zona ini berada di sepanjang pinggiran heliosfer, sebuah gelembung yang disebabkan oleh angin surya. Jaraknya diperkirakan sekitar 80 hingga 100 unit astronomi (AU) dari matahari. Misi penjelajah luar angkasa Voyager 1 dan Voyager 2 saat ini termasuk meneliti heliosheath tersebut. Pada Mei 2005, dilaporkan bahwa Voyag...

Disambiguazione – Flamengo rimanda qui. Se stai cercando altri significati, vedi Flamengo (disambigua). Disambiguazione – Se stai cercando società sportive dal nome simile, vedi Clube de Regatas do Flamengo (disambigua). CR FlamengoCalcio Mengão, Rubro-Negro, O Mais Querido do Brasil (Il più amato del Brasile) Segni distintivi Uniformi di gara Casa Trasferta Terza divisa Colori sociali Rosso, nero Simboli Avvoltoio Dati societari Città Rio de Janeiro (Flamengo) Nazione ...
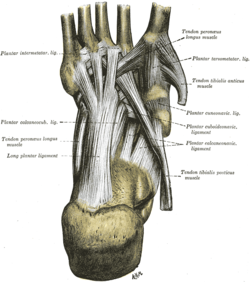
Joint in the foot Cuboideonavicular jointLigaments of the sole of the foot, with the tendons of the fibularis longus, tibialis posterior and tibialis anterior muscles. (Plantar cuboideonavicular ligament labeled at center right.)DetailsIdentifiersLatinarticulatio cuboideonavicularisAnatomical terminology[edit on Wikidata] The cuboideonavicular joint is a joint (articulation) in the foot formed between the navicular bone and cuboid bone. The navicular bone is connected with the cuboid bone...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

In this Spanish name, the first or paternal surname is Rivera and the second or maternal family name is Campesino. Spanish football manager Mario Rivera Rivera in 2022Personal informationFull name Mario Rivera CampesinoDate of birth (1977-08-13) 13 August 1977 (age 46)Place of birth Madrid, SpainHeight 1.72 m (5 ft 8 in)Team informationCurrent team Brunei (head coach)Managerial careerYears Team2007–2009 Leganés (youth)2009–2010 Betis San Isidro2010–2011 Celt...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan hingga 20 Oktober 2024.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Agatha ChelseaChelsea di Idola Cilik 2013LahirAgatha Chels...

Stemma Calcagnini Opere, 1544 Celio Calcagnini (Ferrara, 17 settembre 1479 – Ferrara, 24 aprile 1541) è stato un umanista, diplomatico e astronomo italiano, al servizio del Ducato di Ferrara. Uno dei più dotti sapienti dell'epoca rinascimentale, soldato, ecclesiastico, professore, poeta, filosofo e storico, fu celebrato da Ludovico Ariosto nell'Orlando furioso (XLII.90, XLVI.14), e formulò una teoria sul moto della Terra influenzata da quella copernicana. Indice 1 Biografia e carrier...

For other churches dedicated to St. Paul, see St. Paul's Church (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: St. Paul Church Cambridge, Massachusetts – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this template message) Church in Massachusett...
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Ethnic Arabs who adhere to Islam Arabs who follow Islam Arab Muslimsﺍﻟْمُسْلِمﻴُّﻮﻥ ﺍﻟْﻌَﺮَﺏPopulation of Arab MuslimsRegions with significant populations Arab LeagueLanguagesArabicReligionSunni Islam (majority)Shia Islam (minority)Related ethnic groupsArab Christians and other Arabs Part of a series onArabic culture ArchitectureStyles Islamic Yemeni Nabataean Umayyad Abbasid Fatimid Moorish Mamluk Features Ablaq Alfiz Arabesque Arabic dome Bann...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

海尔·塞拉西一世埃塞俄比亚皇帝統治1930年11月2日-1974年9月12日(43年314天)加冕1930年11月2日前任佐迪图繼任阿姆哈·塞拉西一世(流亡)埃塞俄比亞攝政王統治1916年9月27日-1930年11月2日(14年36天)出生(1892-07-23)1892年7月23日 埃塞俄比亚帝国哈勒爾州逝世1975年8月27日(1975歲—08—27)(83歲) 衣索比亞亚的斯亚贝巴安葬2000年11月5日圣三一大教堂配偶梅南·阿斯福(1889年-1962�...

Klebit Bok Perisai Klebit Bok, dari tahun 1875–1925. Jenis Perisai Negara asal Borneo (Sarawak, Malaysia, Kalimantan Timur & Kalimantan Barat, Indonesia) Sejarah pemakaian Digunakan oleh Suku Dayak Kayan, Suku Dayak Kenyah Spesifikasi Panjang 110–130 cm Klebit Bok atau Kelavit Bok adalah perisai tradisonal suku Kayan dan suku Kenyah di Kalimantan.[1] Deskripsi Klebit Bok adalah perisai berbentuk 'kilau' dan dicat di kedua sisi. Di bagian depannya, sering dilukiskan ...

العلاقات الدومينيكانية الكوستاريكية جمهورية الدومينيكان كوستاريكا جمهورية الدومينيكان كوستاريكا تعديل مصدري - تعديل العلاقات الدومينيكانية الكوستاريكية هي العلاقات الثنائية التي تجمع بين جمهورية الدومينيكان وكوستاريكا.[1][2][3][4][5]...

Building in Manchester, England Gateway HouseGateway House and Piccadilly Station approach pictured in 2011 before the 2017 refurbishmentAlternative namesPiccadilly HouseGeneral informationArchitectural styleModernistLocationPiccadilly, Manchester, EnglandCurrent tenantsemptyCompleted1969Renovated2017OwnerRealty EstatesHeight36 m (118 ft)Technical detailsFloor count9Floor area12,861 m2 (138,430 sq ft)Design and constructionArchitect(s)Richard SeifertReferences[1&#...

Hard Rock CafeJenisSwastaIndustriKafe, restoran, kasino, hotelDidirikanLondon, Inggris14 Juni 1971PendiriIsaac Tigrett dan Peter MortonKantorpusatOrlando, Florida, Amerika SerikatCabang175 (2012)TokohkunciHamish Dodds, Presiden/CEOJohn Galloway, CMOTom Gispanski, CFOPemilikSeminole Tribe of FloridaSitus webhttp://www.hardrock.com Hard Rock Cafe adalah jaringan restoran bertema yang didirikan pada tahun 1971 oleh warga Amerika Serikat Isaac Tigrett dan Peter Morton di London. Pada 1979, kafe t...

Pour les articles homonymes, voir Repentigny. Repentigny Battures du Saint-Laurent à Repentigny. Armoiries Administration Pays Canada Province Québec Région Lanaudière Subdivision régionale L'Assomption Statut municipal Ville Maire Mandat Nicolas Dufour 2021-2025 Code postal J5Y (Nord-est), J5Z (Ouest) et J6A (Sud) FondateurDate de fondation Jean-Baptiste Le Gardeur de Repentigny1670 Constitution 1er juin 2002 Démographie Gentilé Repentignois(e) Population 86 100 hab. (2021)...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juillet 2016). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? C...

Italian cyclist Giovanni MichelettoPersonal informationFull nameGiovanni MichelettoNicknameThe Sacile CountNanèBorn(1889-01-22)22 January 1889Sacile, Kingdom of ItalyDied29 September 1958(1958-09-29) (aged 69)Sacile, ItalyTeam informationDisciplineRoadRoleRiderMajor winsGrand Tours Tour de France 1 individual stage (1913) Giro d'Italia General classification (1912) 2 individual stages (1912) One-day races and Classics Giro di Lombardia (1910) Giro della Romagna (1911) Paris–Menen...

哈馬黑拉島地理位置東南亞坐标0°36′N 127°52′E / 0.600°N 127.867°E / 0.600; 127.867群岛摩鹿加群島面積17,780平方公里(6,860平方英里)面积排名51最高海拔1,635米(5364英尺)最高點甘科諾拉火山管轄 印度尼西亞省北摩鹿加省人口统计人口449,938(2010) 哈马黑拉丛林中的托古蒂尔部落 哈马黑拉岛(Halmahera Island),又名济罗罗岛(Jilolo或Gilolo),是印度尼西亚�...


























































