Read other articles:

Ne doit pas être confondu avec Garde-corps. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (décembre 2019). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Garde du corpsGardes du corps du président fran...

Area code for Western Michigan This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2020) (Learn how and when to remove this template message) Map of area code 616 in Michigan. Area code 616 is the telephone area code in the North American Numbering Plan (NANP) for Greater Grand Rapids, Michigan. The numbering plan area also includes the towns of Holland, ...

Gahwié got’iné, a Sahtú (North Slavey) people of Canada Indigenous people in northern Canada PeopleDeneCountryDenendeh For the Diné people native to the Southwestern US, see Navajo. For other uses, see Dene (disambiguation). Indigenous peoplesin Canada First Nations Inuit Métis History Timeline Paleo-Indians Pre-colonization Genetics Residential schools gravesites Indian hospitals Conflicts First Nations Inuit Truth and Reconciliation Commission Politics Indigenous law British Columbia...

Chemical compound DimesoneClinical dataOther names9α-Fluoro-11β,21-dihydroxy-16α,17α-dimethylpregna-1,4-diene-3,20-dioneDrug classCorticosteroid; GlucocorticoidIdentifiers IUPAC name (8S,9R,10S,11S,13S,14S,16R,17S)-9-Fluoro-11-hydroxy-17-(2-hydroxyacetyl)-10,13,16,17-tetramethyl-6,7,8,11,12,14,15,16-octahydrocyclopenta[a]phenanthren-3-one CAS Number25092-07-3PubChem CID208841ChemSpider180949UNIIB506X74MK0ChEMBLChEMBL2106346Chemical and physical dataFormulaC23H31FO4Molar mass390.495 g...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 1970 في الهندمعلومات عامةالسنة 1970 1969 في الهند 1971 في الهند تعديل - تعديل مصدري - تعديل ويكي بيانات سنوات 1968: 196...

Roberto Ayala Informasi pribadiNama lengkap Roberto Fabián AyalaTanggal lahir 14 April 1973 (umur 51)Tempat lahir Paraná, ArgentinaTinggi 1,7 m (5 ft 7 in)Posisi bermain BekKarier junior Ferro Carril OesteKarier senior*Tahun Tim Tampil (Gol)1991–1994 Ferro Carril Oeste 72 (1)1994–1995 River Plate 40 (0)1995–1998 SSC Napoli 87 (1)1998–2000 A.C. Milan 24 (0)2000–2007 Valencia CF 188 (9)2007 Villarreal CF 0 (0)2007-2009 Real Zaragoza 72 (4)2010 Racing Club de Ave...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (février 2022). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? ...

Ikan Sumatra Status konservasi Aman Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Cypriniformes Famili: Cyprinidae Genus: Puntius Spesies: P. tetrazona Nama binomial Puntius tetrazona(Bleeker, 1855) Sinonim Barbus tetrazona (Bleeker, 1855) Capoeta tetrazona (Bleeker, 1855) Barbodes tetrazona (Bleeker, 1855) Capoeta sumatranus (Bleeker, 1860) Ikan sumatra (Puntius tetrazona) adalah sejenis ikan kecil anggota anak-suku Cyprinidae. Nama tersebut adalah n...

Novel by Gaurav Sharma Long Live the Sullied First editionAuthorGaurav SharmaCountryIndiaLanguageEnglishSubjectNovelGenreFiction, Historical fictionPublishedThink Tank BooksPublication dateJanuary 2020Media typeBookPages236 pagesISBN978-81-9362-049-6OCLC1156173166 Long Live the Sullied is a historical (mythological) novel written by Gaurav Sharma.[1][2] It is the sequel to God of the Sullied and concludes The Sullied Warrior Duology.[3] The book is narrated in a p...

VISA beralih ke halaman ini. Untuk kegunaan lain, lihat Visa (disambiguasi). Visa Inc.Kantor pusat Visa Inc. di Metro Center di Foster CityJenisPublikKode emitenNYSE: VDJIA ComponentS&P 100 ComponentS&P 500 ComponentIndustriJasa keuanganDidirikan1958; 66 tahun lalu (1958) (sebagai BankAmericard)Fresno, California, Amerika SerikatPendiriDee HockKantorpusatFoster City,[1] California, Amerika SerikatWilayah operasiSeluruh duniaTokohkunciAlfred F. Kelly (CEO)ProdukKartu kredi...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أبريل 2024) منتخب هولندا لهوكي الحقل للرجال البلد هولندا  التصنيف بوابة هولندا بوابة هو�...

American politician (born 1955) Not to be confused with Daniel Molloy. Dannel MalloyMalloy in 20166th Chancellor of the University of Maine SystemIncumbentAssumed office July 1, 2019Preceded byJames H. Page88th Governor of ConnecticutIn officeJanuary 5, 2011 – January 9, 2019LieutenantNancy WymanPreceded byJodi RellSucceeded byNed Lamont29th Mayor of StamfordIn officeDecember 1, 1995 – November 30, 2009Preceded byStanley EspositoSucceeded byMichael Pavia Personal det...

Main article: Spokane, Washington Panoramic map of Spokane, 1905 Neighborhoods in Spokane, Washington are officially grouped by the Spokane City Council into three main city council districts: 1, 2, and 3. Each city council district contains multiple, official neighborhoods that are recognized with a neighborhood council. Informally, neighborhoods are colloquially grouped by local geographical, geological, cultural, or historical features (such as South Hill, North Side, Five Mile, Hillyard, ...

U.S. Army Command that runs modernization projects This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (June 2024) (Learn how and when t...

Vice-regal representative Governor of New South WalesStandard of the GovernorIncumbentMargaret BeazleyAC KCsince 2 May 2019ViceregalStyleHer Excellency the HonourableResidenceGovernment House, SydneySeatSydneyAppointerMonarchon the advice of the premierTerm lengthAt His Majesty's pleasure(usually 5 years by convention)Formation7 February 1788First holderArthur PhillipDeputyLieutenant-Governor of New South WalesSalary$529,000Websitegovernor.nsw.gov.au The governor of New South Wales i...

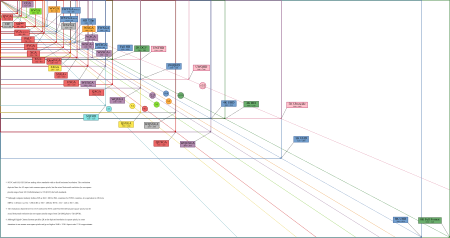
Perbandingan resolusi siaran umum Perbandingan dari resolusi tampilan umum Resolusi 4K mengacu pada resolusi tampilan horizontal sekitar 4.000 piksel.[1] Televisi digital dan sinematografi digital biasanya menggunakan beberapa resolusi 4K yang berbeda. Di televisi dan media konsumen, 3840 × 2160 (4K UHD) adalah standar 4K yang dominan, sedangkan industri proyeksi film menggunakan 4096 × 2160 (DCI 4K). Pangsa pasar televisi 4K meningkat karena harga turun drastis selama 2014[2 ...

بغداد تاريخ بغداد 1831-1917 1831 – 1917 بغداد في يوم 11 أذار - مارس من سنة 1917 م عاصمة بغداد نظام الحكم ولاية الوالي علي رضا باشا 1842-1831 مدحت باشا 1872-1869 جمال باشا 1912-1911 خليل باشا (الأخير) 1917-1915 التاريخ التأسيس 1831 الزوال 1917 اليوم جزء من  العراق تعديل مصدري - تعديل   بغداد في عام 1917 ...

  لمعانٍ أخرى، طالع مقاطعة أونيدا (توضيح). مقاطعة أونيدا     الإحداثيات 42°13′N 112°31′W / 42.21°N 112.52°W / 42.21; -112.52   [1] تاريخ التأسيس 22 يناير 1864  سبب التسمية بحيرة أونيدا  تقسيم إداري  البلد الولايات المتحدة[2]  التقسيم الأعلى أيداهو  العا�...

Jリーグ > 1996年のJリーグ Jリーグシーズン 1996優勝 鹿島アントラーズACC出場 鹿島アントラーズ試合数 240ゴール数 778 (1試合平均3.24)得点王 三浦知良（V川崎・23得点）最大差勝利ホーム試合 V川崎 5-0 鹿島（第30節・11月9日）最大差勝利アウェー試合 柏 0-7 浦和（第20節・9月21日）最多得点試合 福岡 4-5 柏（第17節・8月31日）G大阪 4-5 横浜M（第20節・9月21日）最多観�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) «الرؤية غير الكاملة» هي عبارة تستخدم لوصف نوع محدد ومنتشر ومعقد من تضارب المصالح في أخلاقيات الإعلام، وخ...