Transitive relation
|
Read other articles:
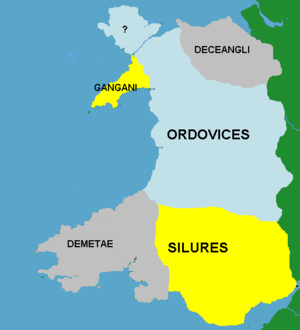
Peta suku di Wales pada masa invasi Romawi. Deceangli atau Deceangi adalah salah satu dari suku Seltik yang tinggal di Britania Raya sebelum invasi Romawi ke Britania. Suku ini tinggal di Wales timur laut. Serangan terhadap suku-suku Wales dilancarkan oleh Publius Ostorius Scapula. Deceangli diserang sekitar tahun 48 AD. Tidak seperti suku Silures dan Ordovices yang melancarkan perlawanan yang panjang, Deceangli menyerah dengan sedikit perlawanan. Pranala luar Deceangi Diarsipkan 2001-12-26 d...

Символы со сходным начертанием: > · 〉 · › · ح · ܓ · ܥ Наконечник стрелки вправо сверху ◌͐˃◌ࣸ Изображение ◄ ◌͌ ◌͍ ◌͎ ◌ ◌͐ ◌͑ ◌͒ ◌͓ ◌͔ ► ◄ ʿ ˀ ˁ ˂ ˃ ˄ ˅ ˆ ˇ ► ◄ ◌ࣴ ◌ࣵ ◌ࣶ ◌ࣷ ◌ࣸ ◌ࣹ ◌ࣺ ◌ࣻ ◌ࣼ ► Характер...

Lebanese Broadcasting Corporation InternationalLogo LBC International NewsDiluncurkan23 Agustus 1985 (jaringan televisi)PemilikGrup pebisnis LebanonSloganEl Dunia Alwan (Arab: الدنيا ألوانcode: ar is deprecated )NegaraLebanonSitus webwww.lbci.com Lebanese Broadcasting Corporation International (Arab: المؤسسة اللبنانية للإرسال انترناسيونالcode: ar is deprecated ), dikenal luas sebagai LBCI, adalah sebuah stasiun televisi swasta di Lebanon. LBCI did...

1973 Spanish filmCount Dracula's Great LoveSpanish theatrical release posterDirected byJavier AguirreWritten byPaul NaschyJavier AguirreAlberto S. InsuaProduced byFrancisco Lara PolopManuel LeguincheStarringPaul NaschyHaydée PolitoffRosanna YanniMirta MillerVictor AlcazarIngrid GarboCinematographyRaúl Pérez CuberoEdited byPetra de NievaMusic byCarmelo A. BernaolaProductioncompaniesJanus FilmsEva FilmMarsk AssociatesMotion Picture MarketingRelease date May 12, 1973 (1973-05-1...

Helen M. Robertsc. 1945Born(1896-01-20)January 20, 1896Toronto, Ontario, CanadaDiedJune 22, 1983(1983-06-22) (aged 87)Los Angeles, California, U.S.Occupation(s)Multilingual literacy educator, writer, photographerSpouse Jewell A. Roberts (m. 1916; died 1952)ChildrenHoward Emery, Walter Kenneth, Ethel Muriel, Lawrence, Blasing, Donald Van Norman Helen Marguerite (Emery) Roberts (January 20, 1896 – June 22, 1983) was an American writer,...

روزا جيانيتا (بالإيطالية: Rosa Giannetta) معلومات شخصية الميلاد 11 أبريل 1945 [1][2] تريفیكو[3] الوفاة 3 يناير 2021 (75 سنة) [4] فورتي دي مارمي[5] سبب الوفاة سرطان الرئة الإقامة فورتي دي مارمي مواطنة إيطاليا الزوج فرانسيسكو ألبيروني [لغات ...

Charlotte Cushman Charlotte Saunders Cushman (Boston, 23 luglio 1816 – Boston, 18 febbraio 1876) è stata un'attrice teatrale statunitense. Indice 1 Biografia 2 Note 3 Bibliografia 4 Voci correlate 5 Altri progetti 6 Collegamenti esterni Biografia Charlotte e Susan in Romeo e Giulietta, 1846 Charlotte Cushman esordì in giovane età come cantante, per poi dedicarsi alla prosa arrivando a ottenere grande successo e consenso nella parti tragiche.[1] Da ricordare una sua interpretazion...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Masjid Al-ZaytunaAgamaAfiliasiIslamStatusAktifLokasiLokasi Tunis, TunisiaArsitekturPeletakan batu pertama698 M.SpesifikasiMenara1Tinggi menara43 meter (141 ft 1 in) Masjid Al-Zaytuna (Arab: جامع الزيتونةcode: ar is deprecated ) ad...

Wireless telecommunication term This article is about mobile phone term. For other uses, see Roaming (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (January 2014) (Learn...

Chemical compound 2-Me-DETClinical dataOther names3-(2-(Diethylamino)ethyl)-2-methylindole; 5-22-10-00158 (Beilstein Handbook Reference); BRN 0166959; Indole, 3-(2-(diethylamino)ethyl)-2-methyl-Identifiers IUPAC name N,N-diethyl-2-(2-methyl-1H-indol-3-yl)ethanamine CAS Number26628-88-6PubChem CID33561ChemSpider30962UNIISSF4F77CV3CompTox Dashboard (EPA)DTXSID30181174 Chemical and physical dataFormulaC15H22N2Molar mass230.355 g·mol−13D model (JSmol)Interactive image SMILES CCN(CC)CCc1c(...

British Field Marshal and politician (1785–1856) Field Marshal The Right HonourableThe Viscount HardingeGCB PC PC (Ire)Governor-General of IndiaIn office1844–1848MonarchQueen VictoriaPrime MinisterSir Robert PeelLord John RussellPreceded byWilliam Wilberforce BirdAs Acting Governor-GeneralSucceeded byThe Earl of DalhousieChief Secretary for IrelandIn office30 July 1830 – 15 November 1830Prime MinisterThe Duke of WellingtonPreceded byLord Francis Leveson-GowerSucceeded byEdward ...

City in Wisconsin, United StatesPrescott, WisconsinCityView of Prescott from park on Point DouglasLocation of Prescott in Pierce County, Wisconsin.Coordinates: 44°45′6″N 92°47′35″W / 44.75167°N 92.79306°W / 44.75167; -92.79306Country United StatesState WisconsinCountyPierceGovernment • TypeMayor - Council • MayorRobert DaughertyArea[1] • Total2.97 sq mi (7.70 km2) • Land2.60&#...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Australian rugby league footballer Brett KimmorleyPersonal informationFull nameBrett KimmorleyBorn (1976-09-15) 15 September 1976 (age 47)Belmont, New South Wales, AustraliaHeight172 cm (5 ft 8 in)Weight91 kg (14 st 5 lb)Playing informationPositionHalfback Club Years Team Pld T G FG P 1995–96 Newcastle Knights 6 1 0 0 4 1997 Hunter Mariners 10 2 4 0 16 1998–00 Melbourne Storm 79 27 27 3 165 2001 Northern Eagles 26 11 0 0 44 2002–08 Cronulla Sharks...

Filipina professional wrestler (born 1988) Gisele ShawShaw posing with the PWE Flame Championship in 2018Born (1988-10-30) 30 October 1988 (age 35)Toledo, Cebu, PhilippinesProfessional wrestling careerRing name(s)AztecaGisele Shaw[1]Reyna ReyesBilled height5 ft 7 in (1.70 m)Billed weight130 lb (9.3 st)Billed fromToledo, Cebu, Philippines [1]Trained byLance StormDebutJanuary 2015 Gisele Mayordo[2] (born 30 October 1988), more known professi...
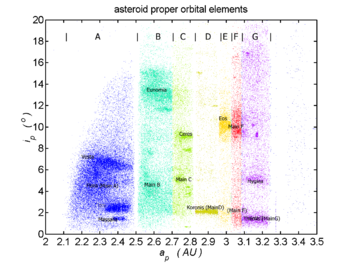
رسم بياني يظهر زاوية الميلان المدارية مقارنةً بنصف المحور الرئيسي لعددٍ من الكويكبات. يمكن رؤية عائلات الكويكبات ككتل منفصلة بألوان مختلفة، تقسمها عن بعضها فجوات كيركوُود المعروفة (A, B+C, D, E+F+G). أسر أو عائلات الكويكبات هي تجمُّعات من الكويكبات (أجرام صخرية صغيرة نسبياً) الت�...

City in Kerala, IndiaThalassery TellicherryCityTLYClockwise from top: Statue of Hermann Gundert, Kalaripayattu, Muzhappilangad Beach, Tellicherry Fort, Theyyam, Thalassery spice market, a cannon inside St. Angelo Fort, Thalassery PierThalasseryThalassery (Kerala)Show map of KeralaThalasseryThalassery (India)Show map of IndiaThalasseryThalassery (Asia)Show map of AsiaThalasseryThalassery (Earth)Show map of EarthCoordinates: 11°44′56.8″N 75°29′20.4″E / 11.749111°N 75...

Disambiguazione – Se stai cercando altri significati, vedi Crise (disambigua). CriseCrise prega Agamennone di rendergli sua figlia Nome orig.Χρύσης Caratteristiche immaginarieSessoMaschile ProfessioneSacerdote di Apollo Crise (in greco antico: Χρύσης?, Chrýsēs) è un personaggio della mitologia greca, sacerdote di Apollo. Indice 1 Genealogia 2 Mitologia 3 Note 4 Bibliografia 5 Altri progetti Genealogia Secondo Eustazio di Tessalonica, il padre di Crise fu Ardi (Ardys). C...

Questa voce sull'argomento calciatori beninesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Djiman KoukouNazionalità Benin Altezza185 cm Calcio RuoloCentrocampista Squadra svincolato CarrieraSquadre di club1 2005-2006 Requins de l'Atlantique50 (7)2007-2009 Soleil37 (5)2009-2010 Évian TG15 (0)2010-2011 Créteil-Lusitanos33 (1)2011-2013 Beira-Mar0 (0)2011-2012→ ...

「BBC」重定向至此。关于其他用法,请见「BBC (消歧义)」。 提示:此条目页的主题不是B2C或BCC。 英國廣播公司British Broadcasting CorporationBBC現行標誌,於2021年10月20日启用BBC廣播大樓夜景(2013年3月29日攝)商业名称BBC公司類型從事公共廣播的法定法人(英语:Statutory corporation)公司前身英國廣播有限公司(英语:British Broadcasting Company)成立1927年1月1日 (1...






























