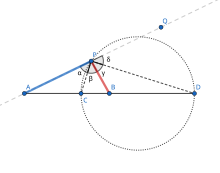
Circles of Apollonius
|
Read other articles:

Stanislav Rostotsky(Станислав Ростоцкий)Stanislav RostotskyLahirStanislav Iosifovich Rostotsky(1922-04-21)21 April 1922Rybinsk, RSFS RussiaMeninggal10 Agustus 2001(2001-08-10) (umur 79)Vyborg, RusiaSuami/istriNina Menshikova Stanislav Iosifovich Rostotsky (bahasa Rusia: Станисла́в Ио́сифович Росто́цкий; 21 April 1922, Rybinsk – 10 Agustus 2001, Vyborg) adalah seorang sutradara Rusia, penerima dua Penghargaan Negara USSR dan sebuah Pen...

ВіттонкурVittoncourt Країна Франція Регіон Гранд-Ест Департамент Мозель Округ Форбак-Буле-Мозель Кантон Фолькемон Код INSEE 57726 Поштові індекси 57580 Координати 49°01′17″ пн. ш. 6°25′50″ сх. д.H G O Висота 221 - 277 м.н.р.м. Площа 9,51 км² Населення 385 (01-2020[1]) Густота 4...

Cet article est une ébauche concernant un explorateur et l’Arctique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Peter Warren DeaseBiographieNaissance 1er janvier 1788Fort MichilimakinacDécès 17 janvier 1863 (à 75 ans)MontréalNationalité canadienneActivité Explorateurmodifier - modifier le code - modifier Wikidata Peter Warren Dease, né le 1er janvier 1788 à Michilimackinac, Michigan aux État...

2014 single by Maroon 5 This article is about the Maroon 5 song. For other uses, see Animal (disambiguation). AnimalsSingle by Maroon 5from the album V ReleasedAugust 25, 2014 (2014-08-25)Studio MXM, Stockholm Conway, Los Angeles Genre Electropop dance-pop pop rock Length3:51Label 222 Interscope Songwriter(s) Adam Levine Shellback Benjamin Levin Producer(s)ShellbackMaroon 5 singles chronology It Was Always You (2014) Animals (2014) Sugar (2015) Music videoAnimals on YouTube Ani...

غابابنتين غابابنتين الاسم النظامي 2-[1-(aminomethyl)cyclohexyl]acetic acid يعالج صرع جزئي، والألم، واضطراب ثنائي القطب، واضطراب القلق الاجتماعي، واستعدادية التهاب المفصل العظمي 1 [لغات أخرى]، وصداع نصفي، وألم عضلي ليفي، ومتلازمة تململ الساقين، وهربس نط�...

Museu Casa do Sertão Museu Casa do Sertão Tipo museu universitário Inauguração 1978 (45 anos) Página oficial (Website) Geografia Coordenadas 12° 12' 3.504 S 38° 57' 58.145 O Localização Feira de Santana - Brasil [edite no Wikidata] Museu Casa do Sertão é um museu localizado dentro do campus da Universidade Estadual de Feira de Santana (UEFS), ao qual pertence, e inaugurado em 30 de junho de 1978; foi construído pelo Lions Clube de Feira de Santana e p...

SimutransCuplikanSimutrans Pak 64 screenshotPengembangMarkus Pristovsek Prissi (kepala pengembangan saat ini)Simutrans Development TeamRilis perdana6 Maret 1999Rilis stabil0.100.0 / 28 Juni 2008Rilis pratayang0.100.1 Repositoriservers.simutrans.org Sistem operasiMulti-platformPlatformAntar-platformTersedia dalamMultibahasaJenisBusiness simulationLisensiArtistic LicenseSitus webSitus Resmi Simutrans Simutrans adalah permainan simulasi antar-platform yang mempunyai tujuan agar pemain dapat menj...

Ini adalah nama Korea; marganya adalah Chun. Chun Myung-hoonInformasi latar belakangLahir6 April 1978 (umur 45)Seoul, Korea SelatanGenreK-pop, pop dansaPekerjaanPenyanyi, rapper, pemeranTahun aktif1996–sekarangLabelMusic Factory EntertainmentGenie MusicArtis terkait NRG HOTSechgodRG Chun Myung-hoonHangul천명훈 Hanja千明勳 Alih AksaraCh'ŏn Myŏng-hunMcCune–ReischauerCheon Myeong-hun Chun Myung-hoon (lahir 6 April 1978) adalah seorang penyanyi, rapper, pemeran dan presenter tele...

Former Australian television channel This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ten Guide – news · newspapers · books · scholar · JSTOR (March 2019) (Learn how and when to remove this template message) Television channel Ten GuideCountryAustraliaBroadcast areaSydney, Melbourne, Brisbane, Adelaide, Perth...

For GiroBank (Denmark 1991-1995), see Danske Bank. National GirobankTypeStatutory corporation (1968) Public limited company (1988)IndustryFinancial servicesFounded1968; 55 years ago (1968)Defunct2003FatePrivatisedSuccessorAlliance & Leicester Commercial BankHeadquartersBootle, MerseysideProductsPostal giro, retail banking National Girobank was a British public sector financial institution run by the General Post Office that opened for business in October 1968.[1]...

Upazila in Rajshahi Division, BangladeshSirajganj Sadar সিরাজগঞ্জ সদরUpazilaJamuna BridgeSirajganj SadarLocation in BangladeshCoordinates: 24°27.5′N 89°42′E / 24.4583°N 89.700°E / 24.4583; 89.700Country BangladeshDivisionRajshahi DivisionDistrictSirajganj DistrictArea • Total325.77 km2 (125.78 sq mi)Population (2011) • Total555,155 • Density1,700/km2 (4,400/sq mi)Time zone...

Untuk kegunaan lain, lihat Gajah Mada. Gajah MadaGenre Drama Roman Laga PembuatMD EntertainmentSutradaraDedy MercyPemeran Rafael P. Ismy Chicco Jerikho Zora Vidyanata Barry Prima Adam Farrel Anne.J.Coto Ryana Dea Ratu Felisha Adhi Pawitra Chilla Irawan Penggubah lagu temaRegina IdolLagu pembukaGajah Mada — Regina IdolLagu penutupGajah Mada — Regina IdolPenata musik Nikanor RS Hariprawiro Iswara Giovani Negara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode178 (daft...

Booklet 3G Тип Нетбук Разработчик Nokia Дата выпуска 24 августа 2009 года Процессор Intel Atom Z530 1.6 ГГц Оперативная память 1 ГБ RAM ОС Windows 7 Медиафайлы на Викискладе Nokia Booklet 3G — первый нетбук фирмы Nokia, анонсированный 24 августа 2009 года[1]. Более подробная информация о нетбуке была...

Stade Mbappé Léppé LocalizaciónPaís CamerúnLocalidad DualaCoordenadas 4°02′41″N 9°41′38″E / 4.04462, 9.69398Detalles generalesNombre completo Stade Samuel Mbappé LéppéNombres anteriores Stade Akwa (1958-1985)Superficie CéspedDimensiones 104 x 66 mCapacidad 4000 espectadoresConstrucciónApertura 1958Remodelación 1965Equipo local Kadji Sports AcademyAcontecimientos clasificación de CAF para la Copa Mundial de Fútbol de 1970[editar datos en ...

Place in Pomeranian Voivodeship, PolandStarogard GdańskiFrom top, left to right: City HallSaint Matthew churchWiechert PalaceMarket SquareSaint Adalbert church FlagCoat of armsStarogard GdańskiCoordinates: 53°58′N 18°32′E / 53.967°N 18.533°E / 53.967; 18.533Country PolandVoivodeship PomeranianCountyStarogardGminaStarogard Gdański (urban gmina)Established1198City rights1348Government • City mayorJanusz StankowiakArea • Total2...

Fields of philosophical, theological, and legal scholarship Part of a series on theCanon law of theCatholic Church Ius vigens (current law) 1983 Code of Canon Law Omnium in mentem Magnum principium Code of Canons of the Eastern Churches Ad tuendam fidem Ex corde Ecclesiae Indulgentiarum Doctrina Praedicate evangelium Veritatis gaudium Custom Matrimonial nullity trial reforms of Pope Francis Documents of the Second Vatican Council Christus Dominus Lumen gentium Optatam totius Orientalium eccle...

Miro開發者Participatory Culture Foundation(英语:Participatory Culture Foundation)首次发布2006年2月21日(0.8.0-rc4)当前版本6.0 (2013年4月5日;穩定版本)[1] 源代码库github.com/pculture/miro 编程语言Python(GTK+)操作系统跨平台类型網絡電視许可协议GNU通用公共许可证网站http://getmiro.com/ Miro(原名為Democracy Player及DTV[2])是由網絡共享文化基金會(英语:Participatory Culture Foundation)開發的集...

「情報衛星」はこの項目へ転送されています。日本に於ける偵察衛星については「情報収集衛星」をご覧ください。 アメリカの偵察衛星 KH-4Bの構造図 偵察衛星(ていさつえいせい)とは、光学機器(望遠レンズ付カメラ)や電波を用いて、地表を観察し地上へ知らせる軍事目的の人工衛星(軍事衛星)である。「スパイ衛星」とも言う。 概要 比較的攻撃を受けにくい...
Paghimo ni bot Lsjbot. 18°16′22″N 76°46′02″W / 18.27268°N 76.76712°W / 18.27268; -76.76712 Pencar River The Pencar River, Pincar River Suba Nasod Jamayka Parokya Parish of Saint Mary Gitas-on 2 m (7 ft) Tiganos 18°16′22″N 76°46′02″W / 18.27268°N 76.76712°W / 18.27268; -76.76712 Timezone EST (UTC-5) GeoNames 3489076 Suba ang Pencar River sa Jamayka.[1] Nahimutang ni sa parokya sa Parish of Saint Mary, sa ...

Catholic ecclesiastical territory Diocese of London, OntarioDiœcesis LondonensisCoat of armsLocationCountry CanadaEcclesiastical provinceOntarioMetropolitanArchdiocese of TorontoDeaneries7StatisticsArea21,349 km2 (8,243 sq mi)The territory comprises the following counties of Ontario: Middlesex, Elgin, Norfolk, Perth, Huron, Lambton, Kent, & Essex.Population- Total- Catholics1,944,182444,310 (22.8%)Parishes131InformationDenominationCatholic ChurchSui iur...

























![{\displaystyle x^{2}+y^{2}=[(d-x)^{2}+y^{2}]\mu ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e050060e3159224d3bad310f31ca46f0ef2036cd)
![{\displaystyle x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc0c5e30a7dafa4b341bce639fb39f52254dc7a)




















