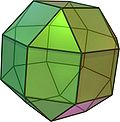
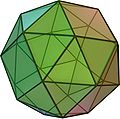
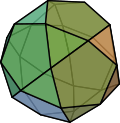
Archimedischer Körper
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

GaroJumlah populasi1,000,000 (2016)Daerah dengan populasi signifikan Meghalaya700,000 Assam29,100 Tripura6,000 Bangladesh210,000BahasaGaroAgamaKekristenan dan Songsa...

لمعانٍ أخرى، طالع كلية طب الأسنان (توضيح). هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2016) كلية طب الأسنان (جامعة البصرة) معلومات الموقع الجغرافي إحصاءات تعديل مصدري - تعديل أسست كلية طب الأسنان ف�...

Real estate services provider Savill redirects here. For people with this name, see Savill (surname). Savills plcCompany typePublic limited companyTraded asLSE: SVSFTSE 250 componentIndustryReal estateFounded1855; 169 years ago (1855)Headquarters33 Margaret Street, London, W1G 0JDKey people Nicholas Ferguson (Chairman) Mark Ridley (CEO) Simon Shaw (CFO) Revenue £2,238.0 million (2023)[1]Operating income £43.3 million (2023)[1]Net income £39.5 million ...

إد أسنر (بالإنجليزية: Ed Asner) معلومات شخصية اسم الولادة (بالإنجليزية: Eddie Asner) الميلاد 15 نوفمبر 1929 كانساس سيتي الوفاة 29 أغسطس 2021 (91 سنة) طارازانا مواطنة الولايات المتحدة عضو في الاشتراكيون الديمقراطيون الأمريكيون الزوجة نانسي سايكس [لغات أخ...
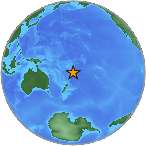
Gempa bumi Tonga 2009Waktu UTC??ISCUSGS-ANSSTanggal *19 Maret 2009 (2009-03-19)Tanggal setempatWaktu setempatKekuatan7.6 MwKedalaman34 kilometer (21 mi)[1]Episentrum23°03′00″S 174°40′05″W / 23.050°S 174.668°W / -23.050; -174.668[1]Wilayah bencana TongaIntensitas maks.VII* Usang Lihat dokumentasi. Gempa bumi Tonga 2009 adalah gempa berkekuatan 7,6 Mw yang terjadi di lepas pantai Tonga pada 19 Maret...

Cet article est une ébauche concernant une localité tchèque. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Dyjákovice Administration Pays Tchéquie Région Moravie-du-Sud District Znojmo Région historique Moravie Maire Josef Gajdošík Code postal 671 26 Démographie Population 861 hab. (2020) Densité 45 hab./km2 Géographie Coordonnées 48° 46′ 18″ nord, 16° 18...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Political party in France Convention of Republican Institutions Convention des institutions républicainesAbbreviationCIRLeaderFrançois MitterrandFoundedJune 1964Dissolved1971Merged intoSocialist PartyIdeologySocialismRepublicanismNational affiliationFGDSPolitics of FrancePolitical partiesElections The Convention of Republican Institutions (French: Convention des institutions républicaines, CIR) was a socialist and republican party in France led by François Mitterrand. The CIR, fo...

CartagenaNama lengkapFútbol Club Cartagena, S.A.D.JulukanEfesé, Aladrokes, Albinegros, Boquerones, CartagosBerdiri25 July 1995; 28 tahun lalu (25 July 1995)as Cartagonova Fútbol ClubStadionCartagonova, Cartagena, Murcia, Spain(Kapasitas: 15,105 [1])PresidentPaco BelmonteHead coachBorja JiménezLigaSegunda División2019-202ªB – Group 4, 1st (promoted)Situs webSitus web resmi klub Kostum kandang Kostum tandang Musim ini Fútbol Club Cartagena, S.A.D. adalah tim sepak bol...

Проверить информацию.Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье.На странице обсуждения должны быть пояснения. Иностранная военная интервенция в РоссииЦентральные державы: Закавказье Дагестан Харьков Антанта: Север России ...

Canadian 2003 children's animated TV series Jacob Two-TwoTitle frame for Jacob Two-TwoAlso known asJacob Jacob (VRAK.TV broadcasts)GenreComedyBased onJacob Two-Twoby Mordecai RichlerDirected by Lan Lamon Helen Lebeau Eric Flaherty Shawn Seles (assistant) Gary Hurst (2nd assistant) Kelvin Smith (art) Voices of Billy Rosemberg Marc McMulkin Kaitlin Howell Jeff Berg Rob Tinkler Jocelyn Barth Harvey Atkin Janet-Laine Green Julie Lemieux Kristopher Clark Dwayne Hill Fiona Reid Howard Jerome Bret T...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Tramway in Brandenburg, Germany Straßenbahn WoltersdorfOperationLocaleWoltersdorf, BrandenburgOpen1913StatusopenLines1Operator(s)Schöneicher – Rüdersdorf Strassenbahn GmbH[1]InfrastructureTrack gauge1,435 mm (4 ft 8+1⁄2 in) standard gaugePropulsion system(s)ElectricElectrification600v DC,[2] Overhead lineStatisticsRoute length5.6km630,000 p.a.[3] Overview WebsiteOfficial website vteWoltersdorf Tramway Legend Reversing Siding S-Bahnhof Rah...

Coupe d'Asie des nations 1964 Généralités Sport Football Organisateur(s) AFC Édition 3e Lieu(x) Israël Date du 26 mai 1964au 3 juin 1964 Participants 4 Palmarès Tenant du titre Corée du Sud (2) Vainqueur Israël (1) Deuxième Inde Troisième Corée du Sud Buts 13 (2,1/match) Meilleur(s) buteur(s) Mordechai Spiegler Inder Singh (2) Navigation Corée du Sud 1960 Iran 1968 modifier La coupe d'Asie des nations de football 1964 est une compétition qui s'est déroulé à Israël en mai 196...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) الدوري السويدي الممتاز 1987 تفاصيل الموسم الدوري السويدي الممتاز النسخة 63 البلد السويد التاريخ �...

11th-century noblewoman This article is about the duchess regnant of Brittany (1066–1072). For her grandmother, duchess consort of Brittany (996–1008), see Hawise of Normandy. Hawise of Rennes (Breton: Hawiz Breizh; French: Havoise de Bretagne) (c. 1024-1037 – 19 August 1072) was Duchess of Brittany from 1066 until her death. Hawise was daughter and heiress of Alan III, Duke of Brittany, by his wife, Bertha of Blois,[1] and as such, a member of the House of Rennes. She had two s...

Selection of the Democratic Party nominee This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1944 Democratic Party presidential primaries – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this message) 1944 Democratic Party presidential primaries ← 1940 March 14 t...

Institut Agama Islam Negeri PonorogoState Islamic Institute of PonorogoNama lainIAIN PonorogoJenisPerguruan tinggi Islam negeri di IndonesiaDidirikan12 Dzulqaidah 1417 H / 21 Maret 1997 M(SK Presiden RI No. 11, tahun 1997)[1]Lembaga indukKementerian Agama Republik IndonesiaAfiliasiIslamAkreditasiBAN-PT: B (2021–2026)[2]RektorDr. Hj. Evi Muafiah, M.Ag.[3]Staf akademik398 (2023)[4]Staf administrasi136 (2023)[4]Jumlah mahasiswa11.784 (2023)[4]Ala...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Constituent Assembly of Italy – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this message) Constituent Assembly Assemblea CostituenteTypeTypeUnicameral HistoryEstablished25 June 1946Disbanded31 January 1948Preceded&...