Conway–Maxwell–Poisson

Funció de probabilitat màssica
Funció de distribució de probabilitat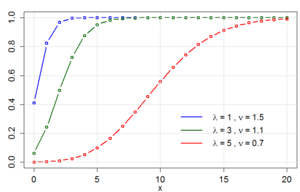
Tipus	família exponencial i distribució univariant
Paràmetres	${\displaystyle \lambda >0,\nu \geq 0}$
Suport	${\displaystyle x\in \{0,1,2,\dots \}}$
fpm	${\displaystyle {\frac {\lambda ^{x}}{(x!)^{\nu }}}{\frac {1}{Z(\lambda ,\nu )}}}$
FD	${\displaystyle \sum _{i=0}^{x}\Pr(X=i)}$
Esperança matemàtica	${\displaystyle \sum _{j=0}^{\infty }{\frac {j\lambda ^{j}}{(j!)^{\nu }Z(\lambda ,\nu )}}}$
Mediana	-
Moda	vegeu text
Variància	${\displaystyle \sum _{j=0}^{\infty }{\frac {j^{2}\lambda ^{j}}{(j!)^{\nu }Z(\lambda ,\nu )}}-\operatorname {mitjana} ^{2}}$
Coeficient de simetria	-
Curtosi	-
Entropia	-
FGM	${\displaystyle {\frac {Z(e^{t}\lambda ,\nu )}{Z(\lambda ,\nu )}}}$
FC	${\displaystyle {\frac {Z(e^{it}\lambda ,\nu )}{Z(\lambda ,\nu )}}}$

En teoria i estadística de probabilitats, la distribució de Conway–Maxwell–Poisson (CMP o COM–Poisson) és una distribució de probabilitat discreta que porta el nom de Richard W. Conway, William L. Maxwell i Siméon Denis Poisson que generalitza la distribució de Poisson afegint un paràmetre. modelar la sobredispersió i la subdispersió. És un membre de la família exponencial,^[1] té la distribució de Poisson i la distribució geomètrica com a casos especials i la distribució de Bernoulli com a cas límit.^[2]

La distribució CMP va ser proposada originalment per Conway i Maxwell el 1962 com una solució per gestionar sistemes de cua amb tarifes de servei depenent de l'estat. La distribució CMP va ser introduïda a la literatura estadística per Boatwright et al. 2003 i Shmueli et al. (2005). La primera investigació detallada sobre les propietats probabilístiques i estadístiques de la distribució va ser publicada per Shmueli et al. (2005). Alguns resultats de probabilitat teòrica de la distribució COM-Poisson són estudiats i revisats per Li et al. (2019), especialment les caracteritzacions de la distribució COM-Poisson.^[3]

La distribució CMP es defineix com la distribució amb funció de massa de probabilitat ^[4]

${\displaystyle P(X=x)=f(x;\lambda ,\nu )={\frac {\lambda ^{x}}{(x!)^{\nu }}}{\frac {1}{Z(\lambda ,\nu )}}.}$

on:

${\displaystyle Z(\lambda ,\nu )=\sum _{j=0}^{\infty }{\frac {\lambda ^{j}}{(j!)^{\nu }}}.}$

La funció ${\displaystyle Z(\lambda ,\nu )}$ serveix com a constant de normalització, de manera que la funció de massa de probabilitat suma un. Tingues en compte que ${\displaystyle Z(\lambda ,\nu )}$ no té una forma tancada.