Tempered representation
|
Read other articles:

Bagian dari serial tentangKeselamatan Konsep umum Eskatologi Keabadian Kebangkitan (orang mati) Keselamatan Kristen Penghakiman khusus Penghakiman Terakhir Soteriologi Transendensi Rekonsiliasi universal Konsep khusus Keadaan antara Kondisionalisme Kristen Memasuki Surga dalam keadaan hidup Satu iman yang benar Hukuman Kematian jiwa Neraka (pandangan Kristen) Purgatorium Penghargaan Surga dalam Kekristenan Dunia yang akan datang lbs Dunia yang akan datang atau zaman yang akan datang adalah fr...

Untuk kegunaan lain, lihat Karanth (disambiguasi). B. V. KaranthLahirBabukodi Venkataramana Karanth(1929-09-19)19 September 1929Babukodi, Manchi, Kerajaan Mysore, India BritaniaMeninggal1 September 2002(2002-09-01) (umur 72)Bangalore, Karnataka, IndiaKebangsaanIndiaPekerjaanKomposer, sutradara, penulis latar, pemeranSuami/istriPrema Karanth (1958−2002; kematiannya) Babukodi Venkataramana Karanth (bahasa Kannada: ಬಾಬುಕೋಡಿ ವೆಂಕಟರಮಣ ಕಾರಂತ್; ...

Saunders Reef State Marine Conservation Area (SMCA) is a marine protected area that extends offshore, just south of Schooner Gulch State Beach and north of Sail Rock in Mendocino County on California’s north central coast. The marine protected area covers 9.35 square miles. Saunders Reef SMCA prohibits the take of all living marine resources, except the commercial and recreational take of salmon by trolling and the commercial take of urchin. Mendocino Coast History Saunders Reef SMCA is one...

1991 edition of the Super Bowl 1991 Super Bowl redirects here. For the Super Bowl that was played at the completion of the 1991 season, see Super Bowl XXVI. Super Bowl XXV Buffalo Bills (1)(AFC)(13–3) New York Giants (2)(NFC)(13–3) 19 20 Head coach:Marv Levy Head coach:Bill Parcells 1234 Total BUF 3907 19 NYG 3773 20 DateJanuary 27, 1991 (1991-01-27)StadiumTampa Stadium, Tampa, FloridaMVPOttis Anderson, running backFavoriteBills by 7[1][2]RefereeJerry SeemanAttendance...

Pour les articles homonymes, voir Tabac (homonymie). Nicotiana tabacum, vue de dessus. Tabac blond séché et haché. Stockage du tabac dans la Tabacalera del Oriente, Tarapoto, Pérou. Le tabac est un produit psychotrope manufacturé élaboré à partir de feuilles séchées de plantes de tabac commun (Nicotiana tabacum), une espèce originaire d'Amérique appartenant au genre botanique Nicotiana (famille : Solanaceae). L'usage du tabac s'est largement répandu dans le monde entier à ...

Television channel Nova ActionCountryCzech RepublicHeadquartersBarrandov, PragueProgrammingLanguage(s)CzechPicture format16:9/4:3 576i (SDTV)1080i (HDTV)OwnershipOwnerCMEKey peopleYoung Active Men Aged 15-54Sister channelsTV NovaNova CinemaNova FunNova GoldNova LadyNova Sport 1Nova Sport 2Nova Sport 3Nova Sport 4Nova Sport 5Nova Sport 6Nova InternationalHistoryLaunched14 July 2012Former namesTV Fanda (2012-2017)AvailabilityTerrestrialDVB-T/T2MUX 24 (FTA)Streaming mediaNova.czWatch live(C...

Species of bird Clay-colored sparrow Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Passeriformes Family: Passerellidae Genus: Spizella Species: S. pallida Binomial name Spizella pallida(Swainson, 1832) The clay-colored sparrow or clay-coloured sparrow[1] (Spizella pallida) is a small New World sparrow of North America. Adults have light brown upperparts and pale under...

7 Light Anti-Aircraft RegimentSANDF 7 Light Anti-Aircraft Regiment emblemActive1 April 1969 - presentCountry South AfricaAllegiance Republic of South Africa Republic of South Africa Branch South African Army South African Army TypeReserve ArtilleryPart of South African Army Air Defence Artillery Formation Army Conventional Reserve Garrison/HQWingfield, Cape TownInsigniaCollar BadgeBursting grenade with seven flamesBeret ColourOxford BlueBattery emblemsBeret ...

I lupanari (dal latino lupa = prostituta) erano, nel corso di tutta l'epoca romana, i luoghi deputati al piacere sessuale mercenario, ovvero delle vere e proprie case di tolleranza. Alcuni sono tuttora visibili nelle rovine dell'antica Pompei.[1][2] Un lupanare negli scavi di Pompei Indice 1 Il culto di Lupa 2 I lupanari di Pompei 3 I bordelli 4 I bordelli a Roma 5 Il giudizio morale 6 Note 7 Bibliografia 8 Voci correlate 9 Altri progetti 10 Collegamenti esterni Il culto di Lu...

Tungusic language of the Russian Far East You can help expand this article with text translated from the corresponding article in Russian. (May 2024) Click [show] for important translation instructions. View a machine-translated version of the Russian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine...

.tmDiperkenalkan30 Mei 1997Jenis TLDTLD kode negara InternetStatusAktifRegistriNIC.TM (dijalankan oleh Internet Computer Bureau)SponsorTM Domain Registry (NetNames)Pemakaian yang diinginkanEntitas yang terhubung dengan TurkmenistanPemakaian aktualDigunakan oleh beberapa situs (tak semuanya dari Turkmenistan)PembatasanTak ada di pendaftaran tingkat kedua. untuk mendaftar di tingkat ketiga, harus menjadi warga negara TurkmenistanStrukturRegistrasi dilakukan di tingkat kedua dan ketigaDoku...
2020年夏季奥林匹克运动会印度尼西亚代表團印度尼西亚国旗IOC編碼INANOC印尼奧林匹克委員會網站nocindonesia.id(英文)(印尼文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員28參賽項目8个大项旗手开幕式:和井田理央(英语:Rio Waida)(冲浪)[1]闭幕式:东京奥组委志愿者[2]獎牌榜排名第55 ...

«Guise» redirige aquí. Para el Almirante Guise, véase Martín Guise. Guisa Entidad subnacional Escudo GuisaLocalización de Guisa en Francia Coordenadas 49°54′01″N 3°37′39″E / 49.900277777778, 3.6275Entidad Comuna de Francia • País Francia • Región Alta Francia • Departamento Aisne • Distrito Vervins • Cantón Guisa (bureau centralisateur) • Mancomunidad Thiérache Sambre et Oise (sede)Alcalde Hugues Cochet (2014-...
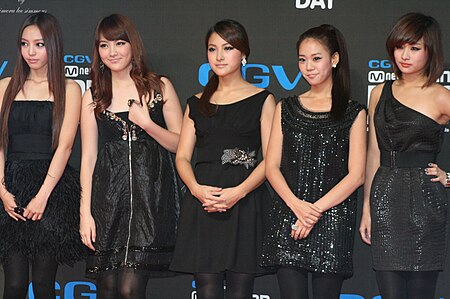
South Korean K-pop girl group KaraKara in 2022From left to right: Seungyeon, Jiyoung, Nicole, Youngji, GyuriBackground informationOriginSeoul, South KoreaGenresK-popJ-popsynth-popR&BelectropopdiscoYears active2007–20162022–presentLabelsDSPRBWMembers Gyuri Seungyeon Nicole Jiyoung Youngji Past members Sunghee[1] Hara Websitekara.bstage.in Kara (Korean: 카라; Japanese: カラ; often stylized in all caps) /ˈkɑːrə/ is a South Korean girl group formed by DSP Media in...

Disambiguazione – Se stai cercando l'omonimo allenatore di pallacanestro sovietico, vedi Vladimir Nikolaevič Obuchov. Questa voce sull'argomento calciatori russi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Vladimir ObuchovNazionalità Russia Altezza184 cm Peso77 kg Calcio RuoloAttaccante Squadra Orenburg CarrieraGiovanili Spartak Mosca Squadre di club1 2008-2013 Spartak Mosc...

United Nations resolution adopted in 1999 UN Security CouncilResolution 1261Former child soldiers in the Democratic Republic of the CongoDate25 August 1999Meeting no.4,037CodeS/RES/1261 (Document)SubjectChildren and armed conflictVoting summary15 voted forNone voted againstNone abstainedResultAdoptedSecurity Council compositionPermanent members China France Russia United Kingdom United StatesNon-permanent members Argentina Bahrain Brazil Cana...

College football game2013 Conference USA Football Championship GameConference Championship Marshall Thundering Herd Rice Owls (9–3) (9–3) 24 41 Head coach: John Doc Holliday Head coach: David Bailiff 1234 Total Marshall 010014 24 Rice 147137 41 DateDecember 7, 2013Season2013StadiumRice StadiumLocationHouston, TexasMVPLuke Turner (RB, Rice)FavoriteMarshall by 6.5RefereeBrad RogersAttendance20,247United States TV coverageNetworkESPN2AnnouncersJoe Tessitore, Matt Millen,...

Peta pembagian administratif tingkat pertama Uruguay Pembagian administratif Uruguay terdiri atas 19 departemen pada tingkat pertama dan 112 munisipalitas pada tingkat kedua. lbsPembagian administratif Amerika Amerika Utara Amerika Selatan Negara berdaulat Amerika Serikat Antigua dan Barbuda Argentina Bahama Barbados Belize Bolivia Brasil Chili Dominica Republik Dominika Ekuador El Salvador Grenada Guatemala Guyana Haiti Honduras Jamaika Kanada Kolombia Kosta Rika Kuba Meksiko Nikaragua Panam...

Hyphanet Informations Créateur Arne Babenhauserheide (d) Première version Mars 2000 Dernière version 0.7.5 build 1497 (4 mars 2023)[1],[2] Dépôt github.com/hyphanet/fred Écrit en Java Système d'exploitation Microsoft Windows, macOS, GNU/Linux et POSIX Environnement Machine virtuelle Java Langues Multilingue Type Logiciel de pair-à-pair (d)Réseau overlaySite d'hébergement de fichiersFilestore (d)Synchronisation de fichiers Licence Licence publique générale GNU, licence MIT, BSD 2-...

عزبة حوض فارس - قرية مصرية - تقسيم إداري البلد مصر المحافظة محافظة البحيرة المركز إيتاي البارود المسؤولون السكان التعداد السكاني 604 نسمة (إحصاء 2006) معلومات أخرى التوقيت ت ع م+02:00 تعديل مصدري - تعديل قرية عزبة حوض فارس هي إحدى القرى التابعة لمركز إيتاي ا�...
