Spherical measure
|
Read other articles:
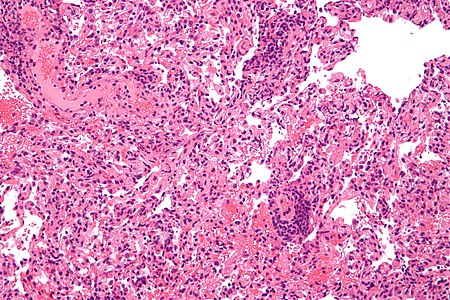
Penolakan transplantasiMikrograf yang menunjukkan penolakan transplantasi paru-paruInformasi umum Penolakan transplantasi terjadi ketika jaringan yang ditransplantasi ditolak oleh sistem imun penerimanya, sehingga jaringan yang ditransplantasi pun rusak. Penolakan transplantasi dapat dikurangi dengan menentukan kemiripan molekuler antara penyumbang dan penerima, serta dengan menggunakan obat imunosupresif seusai transplantasi.[1] Penolakan ini sendiri merupakan respons imun adaptif (m...

Joseph Akpala Informasi pribadiNama lengkap Joseph AkpalaTanggal lahir 24 Agustus 1986 (umur 37)Tempat lahir Jos, NigeriaTinggi 1,85 m (6 ft 1 in)Posisi bermain PenyerangInformasi klubKlub saat ini SV Werder BremenNomor 19Karier junior1999–2002 Pepsi Football Academy2003–2005 Bendel UnitedKarier senior*Tahun Tim Tampil (Gol)2005–2006 Bendel Insurance 19 (13)2006–2008 Charleroi 61 (25)2008–2012 Brugge 102 (38)2012– Werder Bremen 7 (1)Tim nasional‡2008– Nige...

العلاقات الفنزويلية الليبيرية فنزويلا ليبيريا فنزويلا ليبيريا تعديل مصدري - تعديل العلاقات الفنزويلية الليبيرية هي العلاقات الثنائية التي تجمع بين فنزويلا وليبيريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ...

South African swimmer (born 1988) Cameron van der Burghvan der Burgh in the 2008 Summer OlympicsPersonal informationNational team South AfricaBorn (1988-05-25) 25 May 1988 (age 35)Pretoria, South AfricaHeight1.85 m (6 ft 1 in)Weight85 kg (187 lb)SportSportSwimmingStrokesBreaststrokeClubEnergy Standard Medal record Men's swimming Representing South Africa Event 1st 2nd 3rd Olympic Games 1 1 0 World Championships (LC) 2 3 5 World Championships (SC) ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Vahid Halilhodžić Halilhodžić nel 2014 Nazionalità Jugoslavia Bosnia ed Erzegovina (dal 1991) Altezza 182 cm Calcio Ruolo Allenatore (ex attaccante) Termine carriera 1987 - giocatore CarrieraSquadre di club1 1972-1981 Velež Mostar207 (103)1981-1986 Nantes163 (92)1986-1987 Paris Saint-Germain18 (8)Nazionale 1976-1985 Jugoslavia15 (8)Carriera da allenatore 1990-1992 Velež Mostar1993-1994 Beauvais1997-1998 Raja Casablanca1998-2002 Lilla2002-2...

Sanskrit treatise on warfare and archeryDhanurvedaInformationAuthorBhrigu or Vishvamitra or BharadwajaLanguageSanskritPeriod1100 – 800 BCE[1] Dhanurveda (धनुर्वेद) (transl. Science of archery / Knowledge of archery) is a Sanskrit treatise on warfare and archery, traditionally regarded as an upaveda attached to Yajurveda (1100 – 800 BCE) and attributed either to Bhrigu or Vishvamitra or Bharadwaja.[2] It is one among the four upavedas to V...

Antonov An-225 Mriya L'Antonov An-225 dans sa livrée la plus récente, en phase d'atterrissage à l'aéroport international de Manchester (Angleterre), le 24 juin 2013. Rôle Avion de transport Constructeur puis Antonov Équipage 6 Premier vol 21 décembre 1988[1] Retrait Détruit le 27 février 2022 par un bombardement de la fédération de Russie Client principal Antonov Airlines Production 1 exemplaire terminé (1988)(détruit), 1 exemplaire inachevé (état inconnu) Livraisons 1 En serv...

Aubussoncomune Aubusson – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Orne ArrondissementArgentan CantoneFlers-2 TerritorioCoordinate48°47′N 0°33′W / 48.783333°N 0.55°W48.783333; -0.55 (Aubusson)Coordinate: 48°47′N 0°33′W / 48.783333°N 0.55°W48.783333; -0.55 (Aubusson) Superficie3,92 km² Abitanti432[1] (2009) Densità110,2 ab./km² Altre informazioniCod. postale61100 Fuso orarioUTC+1 Codice...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

For the former baseball team, see Vaqueros de Bayamón (baseball). Basketball team in Bayamón, Puerto RicoVaqueros de BayamónLeaguesBaloncesto Superior NacionalFounded1930; 94 years ago (1930)HistoryVaqueros de Bayamón(1930–present)ArenaRuben Rodriguez ColiseumCapacity12,000LocationBayamón, Puerto RicoTeam colorsNavy blue, gold, white Head coachNelson ColónOwnershipYadier MolinaChampionships16 (1933, 1935, 1967, 1969, 1971, 1972, 1973, 1974, 1975, ...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...

U.S. Highway in Wyoming and South Dakota U.S. Route 16US 16 highlighted in redRoute informationLength540 mi[citation needed] (870 km)Existed1926[citation needed]–presentMajor junctionsWest end US 14 / US 20 at Yellowstone National Park entranceMajor intersections US 310 / WYO 789 near Greybull, WY I-25 / US 87 in Buffalo, WY US 85 in Newcastle, WY US 16 Truck in Rapid City, SD East end I-90 ...

静岡県立ふじのくに中学校 磐田本校が入居する「天平のまち」国公私立の別 公立学校設置者 静岡県学区 静岡県全域[1]設立年月日 2023年4月1日共学・別学 男女共学本校 磐田本校分校 三島教室学校コード C122210002643 所在地 〒438-0078[注釈 1] 静岡県磐田市中泉1-6-16(磐田本校)静岡県三島市文教町1丁目3―93(三島教室)[2]外部リンク 公式サイト ウィキポ�...

Chinese calligrapher, politician, and writer of the early Tang dynasty Copy of a text by Ouyang Xun Ouyang Xun (Chinese: 歐陽詢; pinyin: Ōuyáng Xún; Wade–Giles: Ou-yang Hsün; 557–641), courtesy name Xinben (Chinese: 信本; pinyin: Xìn běn; Wade–Giles: Hsin-pên), was a Chinese calligrapher, politician, and writer of the early Tang dynasty. He was born in Hunan, Changsha, to a family of government officials; and died in modern Anhui province. Achievement...

English Midland village in Nottinghamshire, England Village and civil parish in EnglandCar ColstonVillage and civil parishSt Mary's Church, Car ColstonParish mapCar ColstonLocation within NottinghamshireArea2.56 sq mi (6.6 km2)Population171 (2021 Census)• Density67/sq mi (26/km2)OS grid referenceSK 719427• London105 mi (169 km) SSEDistrictRushcliffeShire countyNottinghamshireRegionEast MidlandsCountryEnglandSovereign st...

See also: 1933 Major League Baseball season The following are the baseball events of the year 1933 throughout the world. Overview of the events of 1933 in baseball Years in baseball ← 1930 1931 1932 1933 1934 1935 1936 → 1933 in sports Air sports American football Aquatic sports Association football Athletics Australian rules football Badminton Baseball Basketball Canadian football Chess Climbing Combat sports Sumo Cricket 1932–33 1933 1933–34 Cycling Dance sports Darts Equestrianism ...

Para otros usos de este término, véase Mayapán (desambiguación). Liga de MayapánLuub Mayapan Estado precolombino 1007[2]-1441[1] La Liga de Mayapán en su máxima extensión, hacia el 1200 d. C.Capital Mayapán Uxmal Chichén ItzáEntidad Estado precolombinoIdioma oficial Yucatec, Chontal, Itzá, Mopán, Lakantun, Q'eqchí, Ch'ortí', Sakapulteko, Poqomchí, Uspanteko-Sakapulteko Q'anjob'alReligión Religión mayaPeríodo histórico Período posclásico • 1007[...

Chronologies Chronologie du sport 1951 1952 1953 1954 1955 1956 1957Mois :Jan - Fév - Mar - Avr - Mai - Juin Juil - Aoû - Sep - Oct - Nov - Déc 1953 ◄◄ 1954 en sport ►► 1955 Chronologie dans le monde 1951 1952 1953 1954 1955 1956 1957Décennies :1920 1930 1940 1950 1960 1970 1980Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algé...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Military Administration Nazi Germany – news · newspapers · books · scholar · JSTOR (January 2015) (Learn how and when to remove this message) MilitärverwaltungMilitary AdministrationThe ReichsadlerActive1935 – 1945Country Nazi GermanyAllegianceAdo...

![{\displaystyle \sigma ^{n}(A):={\frac {1}{\alpha (n+1)}}\lambda ^{n+1}(\{tx\mid x\in A,t\in [0,1]\}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5733c8e21d6c8ed6b6b2bc02383f53b50a2290)




