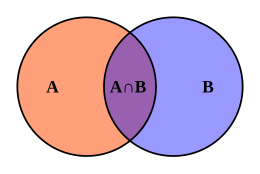
Necessity and sufficiency
|
Read other articles:

In the ShadowPoster filmSutradaraDavid OndříčekDitulis olehMarek EpsteinMisha VotrubaDavid OndříčekPemeranIvan TrojanPenata musikJan P. MuchowMichal NovinskiSinematograferAdam SikoraPenyuntingMichal LánskyTanggal rilis Agustus 2012 (2012-08) Durasi106 menitNegaraRepublik CekoBahasaCekoAnggaranCZK 70 juta In the Shadow (Ceska: Ve stínucode: cs is deprecated ) adalah sebuah film kejahatan Ceko 2012 yqng disutradarai oleh David Ondříček. Film tersebut terpilih sebagao perwa...

German politician You can help expand this article with text translated from the corresponding article in German. (December 2019) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appear...

Gymnasium in North Carolina, USA Belk GymnasiumThe Mine ShaftBelk Gym post-renovationLocationUNC CharlotteCharlotte, North Carolina 28223OwnerUNC CharlotteOperatorUNC CharlotteCapacity3,000ConstructionBroke ground1968Opened1970Closed1996 (for intercollegiate events)TenantsCharlotte 49ers (men) (NCAA) (1970–1976)Charlotte 49ers (women) (NCAA) (1975–1996) Belk Gymnasium, known informally as The Mine Shaft, is a gymnasium on the campus of the University of North Carolina at Charlotte in Char...

Lega Nazionale B 1982-1983Lega Nazionale B Competizione Lega Nazionale B Sport Calcio Edizione 84ª Organizzatore ASF-SFV Luogo Svizzera Partecipanti 16 Formula Girone all'italiana Risultati Vincitore La Chaux-de-Fonds Promozioni La Chaux-de-Fonds Chiasso Retrocessioni Berna Ibach Rüti Cronologia della competizione 1981-1982 1983-1984 Manuale La Lega Nazionale B 1982-1983, campionato svizzero di calcio seconda serie, si concluse con la vittoria del Chaux-de-...

Chemical compound ProtiofateClinical dataATC codeG01AX13 (WHO) Identifiers IUPAC name Dipropyl 3,4-dihydroxy-2,5-thiophenedicarboxylate CAS Number58416-00-5 YPubChem CID68780ChemSpider15070001UNIIFIP88CI9Y3CompTox Dashboard (EPA)DTXSID70207120 Chemical and physical dataFormulaC12H16O6SMolar mass288.31 g·mol−1 (verify) Protiofate is a drug that has [1] antimycotic activity and used in gynecology to treat yeast infections. References ^ Riviera L, Bellot...

弗雷德里克·齊盧巴Frederick Chiluba第2任赞比亚总统任期1991年11月2日—2002年1月2日副职利维·姆瓦纳瓦萨前任肯尼思·卡翁达继任利维·姆瓦纳瓦萨 个人资料出生(1943-04-30)1943年4月30日北罗得西亚基特韦逝世2011年6月18日(2011歲—06—18)(68歲) 尚比亞卢萨卡(Lusaka)墓地 尚比亞卢萨卡使館公園總統陵園(英语:Embassy Park Presidential Burial)国籍赞比亚政党多黨民主運動(MMD)...

BRCW / AEI LionLion in service in 1962Type and originPower typeDiesel-electricBuilderBirmingham Railway Carriage and Wagon Company and AEI LtdSerial numberDEL260Build date1962SpecificationsConfiguration: • UICCo′Co′ • CommonwealthCo-CoGauge1,435 mm (4 ft 8+1⁄2 in) standard gaugeWheel diameter3 ft 9 in (1.143 m)Wheelbase50 ft 9 in (15.47 m)Length63 ft 6 in (19.35 m)Width8 ft 10 ...

جوني ديب (بالإنجليزية: Johnny Depp) جوني ديب في عام 2019 معلومات شخصية اسم الولادة جون كريستوفر ديب الثاني الميلاد 9 يونيو 1963 (العمر 60 سنة)أوينسبورو، كنتاكي، الولايات المتحدة الإقامة لوس أنجلوس مواطنة الولايات المتحدة لون الشعر شعر بني الطول 1.78 م (5 قدم 10 بوصة) اس...

الصليب الحقيقيمعلومات عامةيوم العيد 3 مايو14 سبتمبر أحداث مهمة صلب يسوع Finding of the True Cross (en) الشكل صليب لديه جزء أو أجزاء fragment of the True Cross (en) تعديل - تعديل مصدري - تعديل ويكي بيانات لوحة (العثور على الصليب الحقيقي) للرسام اغنولو جادي، فلورنسا، 1380 الصليب الحقيقي هو اسم لبعض القطع ال...

Динатрон А. Галла конструкции 1918 года Динатронный эффект в электронных лампах — «переход электронов вторичной эмиссии на другой электрод».[1] Бомбардировка анода лампы электронами высокой энергии выбивает из него электроны вторичной эмиссии. Если при этом на друго�...

National recreation area in the United States Bighorn Canyon National Recreation AreaSnowfall on the Bighorn Canyon in the North DistrictShow map of MontanaShow map of the United StatesLocationBig Horn and Carbon counties, Montana & Big Horn County, Wyoming, USANearest cityBillings, MontanaCoordinates45°11′40″N 108°7′50″W / 45.19444°N 108.13056°W / 45.19444; -108.13056Area120,296.22 acres (486.8215 km2)[1]EstablishedOctober 15, 1966Vis...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Politics of Equatorial Guinea – news · newspapers · books · scholar · JSTOR (December 2008) (Learn how and when to remove this message) Politics of Equatorial Guinea Constitution Human rights Government President T. Obiang Nguema Mbasogo Vice President T. Ngue...

Species of butterfly Neptis sankara Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Nymphalidae Genus: Neptis Species: N. sankara Binomial name Neptis sankara(Kollar, [1844]) Synonyms Limenitis sankara Kollar, [1844] Neptis amba Moore, 1858 Neptis quilta Swinhoe, 1897 Limenitis antonia Oberthür, 1876 Neptis sankara, the broad-banded sailer, is a species of nymphalid butterfly found in the Indomalayan realm. At th...

1972 studio album by Dr. Hook & the Medicine ShowSloppy SecondsStudio album by Dr. Hook & the Medicine ShowReleased1972GenreCountry rockLength35:55LabelColumbiaProducerRon HaffkineDr. Hook & the Medicine Show chronology Doctor Hook(1972) Sloppy Seconds(1972) Belly Up!(1973) Professional ratingsReview scoresSourceRatingAllMusic[1] Sloppy Seconds was the second album from the country rock band Dr. Hook & the Medicine Show. It featured some of their most popular s...

1996 novella by Joyce Carol Oates First Love: A Gothic Tale First editionAuthorJoyce Carol OatesIllustratorBarry MoserLanguageEnglishGenreGothic novelPublisherEcco PressPublication date1996Publication placeUnited StatesMedia typePrint (Hardback & Paperback)Pages85 ppISBN0-88001-457-1OCLC33165822Dewey Decimal813/.54 20LC ClassPS3565.A8 F57 1996Preceded byZombie Followed byWe Were the Mulvaneys First Love: A Gothic Tale is a novella by American novelist and es...

تاريخ الجغرافياصنف فرعي من تاريخ العلوم الاجتماعية يمتهنه historian of geography (en) الموضوع جغرافيا تعديل - تعديل مصدري - تعديل ويكي بيانات يشمل تاريخ الجغرافيا مختلف تواريخ الجغرافيا التي اختلفت بمرور الزمان وباختلاف الجماعات الثقافية والسياسية. وبعد التطورات الأخيرة، أصبحت الجغ...

Football tournament season 1894–95 FA CupThe Aston Villa team following the finalTournament detailsCountry England WalesDefending championsNotts CountyFinal positionsChampionsAston Villa (2nd title)Runner-upWest Bromwich Albion← 1893–941895–96 → The 1894–95 FA Cup was the 24th season of the world's oldest association football competition, the Football Association Challenge Cup (more usually known as the FA Cup). The cup was won by Aston Villa, who ...

У этого человека испанская фамилия; здесь Торрес — фамилия отца, Падилья — фамилия матери. Эрик Торрес Общая информация Полное имя Эрик Эстефано Торрес Падилья Прозвище El Cubo[1][2] Родился 19 января 1993(1993-01-19)[3] (31 год)Гвадалахара, Мексика Гражданство Мексик...

Portion of a company's equity This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Share capital – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this message) Share certificate of the Boston American League Base-Ball Club shows a capital stock of 100 000$ A corporation's sha...

Questa voce sull'argomento calciatori vietnamiti è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Phạm Thành LươngNazionalità Vietnam Altezza164 cm Peso59 kg Calcio RuoloCentrocampista Squadra Hà Nội T&T CarrieraSquadre di club1 2006-2008 Hà Nội ACB? (?)2009 The Vissai N.B.? (?)2010-2011 Hà Nội ACB24+ (6+)2012 Hà Nội24 (4)2013- Hà Nội T&T186 (13) Nazionale 2008-2016 Vietnam78 (7) 1 I due n...