Kodaira vanishing theorem
|
Read other articles:

iPod touchcomputeriPod Touch di 7ª generazione in colorazione rosaTipoLettore multimediale Paese d'origine Stati Uniti ProduttoreApple Inc. Presentazione5 settembre 2007 Fine vendita10 maggio 2022 CPUApple A4, Apple A5, Apple A8 e Apple A10 Fusion SO di serieiOS Sito webwww.apple.com/it/ipod-touch/ Modifica dati su Wikidata · Manuale L'iPod touch è stato un lettore multimediale dotato di touch screen realizzato da Apple e presentato il 5 Settembre 2007. Come gli altri membri ...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (May 2014) (Learn how and when to remove this template message) In this Spanish name, the first or paternal surname is Sánchez de Tagle and the second or maternal family name is de la Rasa. Don Luis Sánchez de Tagle y de la Rasa, 1st Marquis of Altamira (1642 - 1710...

Bupati PacitanLambang Kabupaten PacitanPetahanaIndrata Nur Bayuajisejak 26 April 2021KediamanKantor Bupati PacitanMasa jabatan5 tahunDibentuk1745Pejabat pertamaR. T. NotopoeroSitus webpacitankab.go.id Berikut Daftar Nama Bupati Pacitan dari masa ke masa. No Nama Masa Jabatan Keterangan 1 R. T. Notopoero 1745 - 1750 R. T. Notopoero 1750 - 1757 Kali kedua menjabat 2 R.T. Soerjonegoro I 1757 - 1757 3 R.T. Setrowidjojo II 1757 - 1812 4 Mas Tumenggung Djogokaryo I (Pancogomo) 1812 - 1826 5 Ma...

Portuguese international television channel Television channel RTP InternacionalCountryPortugalBroadcast areaEuropeNorth AmericaSouth AmericaAustraliaAsiaMiddle EastAfricaProgrammingPicture format576i (16:9 SDTV)OwnershipOwnerRádio e Televisão de PortugalSister channelsRTP1RTP2RTP3RTP DesportoRTP MemóriaRTP AçoresRTP MadeiraRTP ÁfricaHistoryLaunched10 June 1992; 31 years ago (1992-06-10)LinksWebsiteRTPiAvailabilityTerrestrialDigital terrestrial television (Andorra)Chann...

Men's 5000 metres at the 1983 World ChampionshipsVenueHelsinki Olympic StadiumDates10 August (heats)12 August (semi-finals)14 August (final)Competitors39Winning time13:28.53 CRMedalists Eamonn Coghlan Ireland Werner Schildhauer East Germany Martti Vainio Finland1987 → Events at the1983 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen3000 mwomen5000 mmen10,000 mmen100 m hu...

Podocarpaceae Daun dan runjung biji tua Podocarpus macrophyllus Klasifikasi ilmiah Kerajaan: Plantae Divisi: Pinophyta Kelas: Pinopsida Ordo: Pinales Famili: PodocarpaceaeEndl. Genera Acmopyle Afrocarpus Dacrycarpus Dacrydium - cin atau sempilor Falcatifolium Halocarpus Lagarostrobos Lepidothamnus Manoao Microcachrys Microstrobos Nageia Parasitaxus Phyllocladus Podocarpus Prumnopitys Retrophyllum Saxegothaea Sundacarpus Podocarpaceae atau Suku Melur-meluran adalah satu famili besar dari koni...
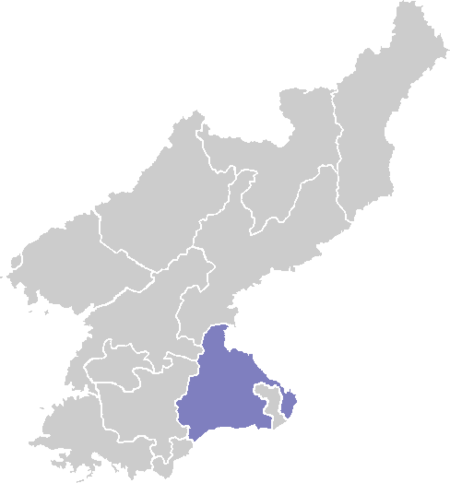
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Munchon – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this template message) Municipal City in Kangwon Province, North KoreaMunch'ŏn 문천시Municipal CityKorean transcription(s) • Chosŏn'gŭl문�...

Questa voce o sezione sull'argomento società calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Red Bull GhanaCalcio Red Bulls Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Bianco, rosso Simboli Tori Dati societari Città Sogakope Nazione Ghana Confederazione CAF Federazi...

Pour les articles homonymes, voir Charlotte. Charlotte La grande-duchesse Charlotte de Luxembourg au début des années 1940. Titre Grande-duchesse de Luxembourg 15 janvier 1919 – 12 novembre 1964 (45 ans, 9 mois et 28 jours) Couronnement 15 janvier 1919 (prestation de serment) Président du gouvernement Émile Reuter Pierre Prüm Joseph Bech Pierre Dupong Joseph Bech Pierre Frieden Pierre Werner Prédécesseur Marie-Adélaïde Successeur Jean Héritière présomptive du tr�...

Japanese biochemist Osamu Hayaishi早石 修Born(1920-01-08)January 8, 1920Stockton, California, USADiedDecember 17, 2015(2015-12-17) (aged 95)Kyoto, JapanNationalityJapaneseAlma materOsaka UniversityKnown forOxygenasesProstaglandinAwardsJapan Academy Prize (1967) Order of Culture (1972) Wolf Prize (1986)Scientific careerFieldsBiochemistryPhysiologyInstitutionsOsaka Bioscience InstituteOsaka Medical CollegeKyoto UniversityVanderbilt UniversityUniversity of TokyoOsaka University...

Stadium in Santa Barbara, California, US Harder StadiumSoccer HeavenAugust 2018Santa BarbaraLocation in the United StatesShow map of the United StatesSanta BarbaraLocation in CaliforniaShow map of CaliforniaFull nameMeredith Fieldat Harder StadiumFormer namesCampus Stadium(1966–1981)AddressStadium RoadLocationUniversity of California, Santa BarbaraCalifornia, U.S.Coordinates34°25′12″N 119°51′14″W / 34.42°N 119.854°W / 34.42; -119.854Public transitEl Coleg...

Campionato mondiale di Formula 1 2002Edizione n. 53 del Campionato mondiale di Formula 1 Dati generaliInizio3 marzo Termine13 ottobre Prove17 Titoli in palioPiloti Michael Schumachersu Ferrari F2001B e Ferrari F2002 Costruttori Ferrari Altre edizioniPrecedente - Successiva Edizione in corso Il campionato mondiale di Formula 1 2002 organizzato dalla FIA è stata, nella storia della categoria, la 53ª stagione ad assegnare il Campionato Piloti, vinto da Michael Schumacher, e la 45ª ad...

International ice hockey competition 2014 IIHF Women's Challenge Cup of AsiaTournament detailsHost country ChinaVenue(s)1 (in 1 host city)Dates9–13 March 2014Teams4Final positionsChampions China (2nd title)Runner-up North KoreaThird place South KoreaTournament statisticsGames played8Goals scored36 (4.5 per game)Attendance1,817 (227 per game)← 20122017 → The 2014 IIHF Women's Challenge Cup of Asia was an int...

Overview of the architecture in London A 2014 cityscape of London viewed from Westminster, showing an eclectic array of historic and modern architecture including the Palace of Westminster and The Shard. London's architectural heritage involves many architectural styles from different historical periods. London's architectural eclecticism stems from its long history, continual redevelopment, destruction by the Great Fire of London and The Blitz, and state recognition of private property right...
Création automatique ou semi-automatique. Cet article a été créé automatiquement par DickensBot. Il peut contenir, entre autres, des erreurs linguistiques ou un choix bizarre d'images. Il doit être (re)vérifié par un être humain.Le modèle peut être retiré après inspection du contenu. Plus d'articles avec ce bandeau dans la catégorie dédiée. Les erreurs systématiques suspectes peuvent être signalées sur Wikipédia:Bot/Requêtes, ou sur la page de discussion de l’utilisate...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 1912 في الولايات المتحدةمعلومات عامةالسنة 1912 1911 في الولايات المتحدة 1913 في الولايات المتحدة تعديل - تعديل م�...

Genus of bees Tetrapedia Tetrapedia sp. (female) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Hymenoptera Family: Apidae Tribe: Tetrapediini Genus: TetrapediaKlug, 1810 Species ~13 species Synonyms Tetrapedium Berthold, 1827 Lagobata Smith, 1861 Tetrapaedia Dalla Torre, 1896 The genus Tetrapedia contains approximately 13 species of small apid bees occurring in the Neotropics (from Mexico to Argentina), and they are unusual in possessin...
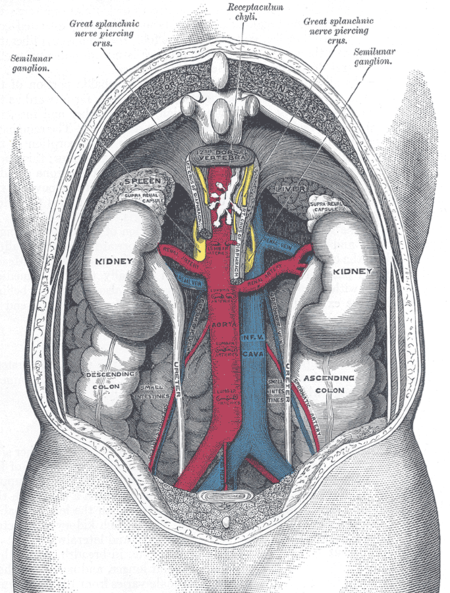
Anatomical space in the abdominal cavity behind the peritoneum Retroperitoneal spaceHorizontal plane through the kidneys, showing subdivisions of the retroperitoneal space. The anterior and posterior pararenal spaces have been exaggerated to provide representation of their relation to other retroperitoneal structures.Human kidneys viewed from behind with spine removedDetailsIdentifiersLatinspatium retroperitonealeMeSHD012187TA98A10.1.01.002TA23814FMA15080Anatomical terminology[edit on Wik...

Justus D. BarnesBarnes dalam The Great Train Robbery (1903)Lahir(1862-10-02)2 Oktober 1862Little Falls, New York, Amerika SerikatMeninggal6 Februari 1946(1946-02-06) (umur 83)Weedsport, New York, Amerika SerikatMakamWeedsport Rural CemeteryPekerjaanPemeranTahun aktif1903–1917 (film) Justus D. Barnes (2 Oktober 1862 – 6 Februari 1946), atau disebut juga sebagai George Barnes dalam beberapa sumber, adalah seorang pemeran panggung dan film Amerika Serikat. Ia dikenal...

Protected Wilderness in West Virginia, United States Big Draft WildernessIUCN category Ib (wilderness area)[1]Big Draft Wilderness sign in 2013Location of Big Draft Wilderness in West VirginiaLocationGreenbrier, West Virginia, United StatesCoordinates37°55′15″N 80°15′55″W / 37.92083°N 80.26528°W / 37.92083; -80.26528Area5,144 acres (20.82 km2)[2]Elevation1,920 ft (590 m)Established2009-03-30OperatorMonongahela National ForestW...





