Smooth morphism
|
Read other articles:

Kesucian PrasastiGenreDramaSkenarioNicke RachmaSutradaraSonu S.Pemeran Ayu Azhari Gunawan Cut Sarra Alda Risma Rima Melati Frans Tumbuan Mega Utami Vicky Burky Baron Hermanto Eksanti Achmad Yusuf Atalarik Syach Penggubah lagu temaChossy PratamaPenata musikChossy PratamaNegara asalIndonesiaJmlh. episode30ProduksiProduser eksekutifSoebagio SamtaniProduserGope T. SamtaniDurasi60 menitRilis asliJaringanIndosiarRilis30 September 1999 (1999-09-30) –11 Mei 2000 (2000-5-11) Ke...

Pour les articles homonymes, voir Dujardin-Beaumetz et Beaumetz (homonymie). Étienne Dujardin-BeaumetzÉtienne BeaumetzPortrait gravé d'Étienne Dujardin-Beaumet, publié dans l’Album Mariani (1906).FonctionsSénateur de l'Aude7 janvier 1912 - 27 septembre 1913Député de l'Audeà partir de 1889Conseiller général de l'AudeCanton de Limouxà partir de 1886BiographieNaissance 29 septembre 1852PassyDécès 27 septembre 1913 (à 60 ans)La BezoleSépulture La BezoleNom de naissance Hen...

Fathul Mu'in Daeng MaggadingLahir(1919-12-17)17 Desember 1919Pakalli, Maros, Hindia BelandaMeninggal18 September 1985(1985-09-18) (umur 65)Kuri, Kabupaten Maros, Sulawesi Selatan, IndonesiaMakamPemakaman Umum MarosKebangsaanIndonesiaAlmamaterMULO (SMP zaman Hindia Belanda)PekerjaanPemuka AgamaDikenal atasPejuang KemerdekaanTokoh Muhammadiyah Sulawesi SelatanSuami/istriHj. Badate (Istri Pertama)Hj. Rahmah Masbah (Istri Kedua)Anak8Orang tuaH. Malawi (Ayah)Hj. Husna (Ibu) Mayor K.H. Fathul...

Untuk Carleton College di Northfield, Minnesota, Amerika Serikat, lihat Carleton College. Carleton UniversityMotoOurs the Task Eternal[1]Jenisuniversitas swastaDidirikan1942AfiliasinondenominasiDana abadiCA$230 juta[2]KanselirDr Marc GarneauPresidenDr Roseann RunteStaf administrasi3.568Sarjana20.901 [3]Magister3.362 [3]Alumnilebih dari 100,000LokasiOttawa, Ontario, KanadaKampuspinggir kota, 62 hektaretim olahragaCarleton RavensWarna ...

2009 single by Jennifer HudsonGiving MyselfSingle by Jennifer Hudsonfrom the album Jennifer Hudson ReleasedJune 2, 2009GenreSoulpopLength4:15LabelArista, JSongwriter(s)Robin ThickeProducer(s)Robin Thicke, Pro JayJennifer Hudson singles chronology If This Isn't Love (2009) Giving Myself (2009) Where You At (2011) Giving Myself is a song recorded by American recording artist Jennifer Hudson. It was written and produced by singer-songwriter Robin Thicke, along with his frequent co-producer Pro J...

This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. Sarcoprion edax This list of prehistoric cartilaginous fish genera is an attempt to create a comprehensive listing of all genera that have ever been included in the class chondrichthyes and are known from the fossil record. This list excludes purely vernacular terms, genera that are now considered invalid, doubtful (nomina dubia), or were ...

Swedish clergyman (1417–1467) This article incorporates unedited text from the public-domain Catholic Encyclopedia. It may be out of date, or may reflect the point of view of the Catholic Church as of 1913. It should be edited to reflect broader and more recent perspectives. (January 2021) Jöns BengtssonArchbishop of UppsalaPrimate of SwedenSeal of Archbishop Jöns Bengtsson, displaying the arms of the Archdiocese of Uppsala (left) and the Oxenstierna family (right)ChurchRoman CatholicArch...

Fotografía de pintura de animales de Lascaux. Este artículo detalla una cronología de la historia de la zoología. En la prehistoria El hombre inició la zoología en la prehistoria: a medida que tenía contacto con los seres vivos (en especial los animales) los fue conociendo y utilizando de acuerdo a sus necesidades. La calidad de los conocimientos que tenía acerca de la naturaleza se encuentra en las pinturas rupestres dejadas en cavernas por el hombre de Cro-Magnon. Con la domesticaci...
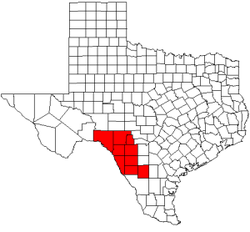
Middle Rio Grande Development CouncilLogoMap of Texas highlighting counties served by the Middle Rio Grande Development CouncilFormationMarch 1970TypeVoluntary association of governmentsRegion served 14,333 sq mi (37,120 km2)Membership 9 counties Historical populationYearPop.±%2000154,381— 2010167,010+8.2%2020162,295−2.8%Source: [1][2] The Middle Rio Grande Development Council (MRGDC) is a voluntary association of cities, counties and...

Leader of Cuba from 2011 to 2021 This article is about the former First Secretary of the Communist Party of Cuba and former President of Cuba. For the former Governor of Arizona, see Raúl Héctor Castro. For other people, see Raúl Castro (disambiguation). In this Spanish name, the first or paternal surname is Castro and the second or maternal family name is Ruz. Raúl CastroCastro in 2016First Secretary of the Communist Party of CubaIn office19 April 2011 – 19 April 2021P...

For the city, see Tarnobrzeg. Republic of TarnobrzegRepublika Tarnobrzeska (Polish)1918–1919CapitalTarnobrzegCommon languagesPolishReligion CatholicismGovernmentRepublica• President Tomasz Dąbal (last) Historical eraAftermath of World War I• Established 6 November 1918• Disestablished Spring 1919 Preceded by Succeeded by Kingdom of Galicia and Lodomeria Second Polish Republic Today part ofPolanda. Soviet republic intended.The Republic of Tarnobrzeg (Polish: R...

Président du Congrès des députésPresidente del Congreso de los Diputados Armoiries du Congrès des députés Titulaire actuelleFrancina Armengoldepuis le 17 août 2023 Création 24 septembre 1810 Titre Excelentísima Señora Mandant Congrès des députés Durée du mandat 4 ans, renouvelable Premier titulaire Ramon Llàtzer de Dou i de Bassols Résidence officielle Palais des Cortès, Madrid Rémunération 230,926.48 € annuellement [1] Site internet www.congreso.es modifier Le pr...

1994 Filipino film by Kidlat Tahimik Why Is Yellow the Middle of the Rainbow?Japanese-language release posterDirected byKidlat TahimikWritten byKidlat TahimikKidlat Gottlieb KalayaanKawayan Thor KalayaanKabunian Cedric EnriqueCinematographyKidlat TahimikEdited byKidlat TahimikMaureen Gosling (First Assembly)ProductioncompanyThird World ProjectorRelease date 1994 (1994) Running time175 minutesCountryPhilippinesLanguagesEnglishFilipino Why Is Yellow the Middle of the Rainbow? (Filipino: Ba...

سعيد بن يزيد بن مسلمة الأزدي معلومات شخصية اسم الولادة سعيد بن يزيد بن مسلمة الإقامة البصرة الكنية أبو مسلمة اللقب الأزدي الطاحي البصري القصير الحياة العملية الطبقة من التابعين، طبقة ابن شهاب الزهري المهنة مُحَدِّث تعديل مصدري - تعديل سعيد بن يزيد بن مسلمة الأز�...

الدوري الإسكتلندي الدرجة الرابعة 2011–12 تفاصيل الموسم الدوري الإسكتلندي الدرجة الرابعة [لغات أخرى] البلد المملكة المتحدة الدوري الإسكتلندي الدرجة الرابعة 2010–11 الدوري الإسكتلندي الدرجة الرابعة 2012–13 تعديل مصدري - تعديل الدوري الإسكتلندي الدرجة ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. A-Rosa Brava on the Rhine River in Cologne Sejarah Nama A-Rosa BravaPemilik 2011–2012: A-ROSA FlussschiffOperator A-ROSA FlussschiffRegistrasi Rostock, JermanPembangun Neptun Werft, Warnemünde, JermanNomor galangan S.516Pasang lunas 28 J...

Cabinet of the Kingdom of Saudi Arabia Politics of Saudi Arabia Member State of the Arab League Basic Law Monarchy King and Custodian of the Two Holy Mosques Salman Crown Prince Mohammed bin Salman Deputy crown prince Vacant Allegiance Council Succession Government Prime Minister Mohammed bin Salman Council of Ministers Consultative Assembly President: Abdullah ibn Muhammad Al ash-Sheikh National Security Council Legal system The Quran The Hadith Judiciary Capital punishment Freedom of religi...

Ancient Greek god of marriage ceremonies For other uses, see Hymen (disambiguation). HymenaiosGod of weddings, reception, and marriageMember of the ErotesHymen depicted on a Roman mosaic, Ostia AnticaAbodeMount OlympusSymbolBridal torchParentsMagnes and Calliope[1]Apollo and CalliopeApollo and Clio Apollo and Terpsichore Apollo and Urania Dionysus and unknown mother[2]Dionysus and Ariadne[3]EquivalentsRoman equivalentTalasius Nicolas Poussin, Hymenaios Disguised as a W...

Questa voce sugli argomenti porte cittadine e Siena è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Porta San MarcoPorta San Marco vista dall'esterno della cittàUbicazioneStato Italia CittàSiena Coordinate43°18′42.98″N 11°19′30.9″E43°18′42.98″N, 11°19′30.9″E Informazioni generaliTipomura Costruzione1325-1326 voci di architetture militari presenti su Wikipedia Modifica dati su Wikidata · Manuale Porta San Marco vista da...

親任官の位置づけ 親任官(しんにんかん)は、1886年(明治19年)に設けられた官吏の分類の一つで[1]、1890年(明治23年)から明治憲法の下で用いられ1948年(昭和23年)に廃止した[2]。官僚制度における最高の位置付けにあり高等官の中の勅任官に含まれた。天皇の親任式を経て任命され、官記には天皇が親署する。親任官と勅任官に対しては、敬称に閣下を...









![{\displaystyle B=A[t_{1},\dots ,t_{n}]/(P_{1},\dots ,P_{m})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bba842ca6591c40252716975ba6e6eaab353160)



![{\displaystyle {\text{Spec}}_{\mathbb {C} }\left({\frac {\mathbb {C} [x,y]}{(f=y^{2}-x^{3}-x-1)}}\right)\to {\text{Spec}}(\mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b52aff8ea7d9bfc7a4ef637bae5f9bf151ff13)
![{\displaystyle [3x^{2}-1,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3d90a6889cb2edd6eb90095f6808e1bd4c4fbc0)







![{\displaystyle O(k)=\mathbb {P} (1,\ldots ,1,k)-\{[0:\cdots :0:1]\}\to \mathbb {P} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c83ffbdefab8e1c27598ebffbc872d53aae967)
![{\displaystyle [x_{0}:\cdots :x_{n}:x_{n+1}]\to [x_{0}:\cdots :x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7797f1282119989bfc73904a99ab31cee66f5fb)



![{\displaystyle L={\frac {K[x]}{(f(x))}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73819f6dc53c5ec57c924152260251d854844ea0)










![{\displaystyle {\text{Proj}}\left({\frac {\mathbb {C} [x,y]}{(x^{4}+y^{4})}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c0db08521734a7a2fb470becb302d92fd17313)
![{\displaystyle {\text{Proj}}\left({\frac {\mathbb {C} [x,y,z]}{(x^{4}+y^{4})}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12ec315c09200e05932cb65c576508d5758fe1c3)

![{\displaystyle {\text{Spec}}\left({\frac {\mathbb {C} [X,Y]}{(X^{4}+Y^{4})}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2b909c77b3d5639f8e0e3bb001896d8d0ddd98)

![{\displaystyle {\text{Spec}}\left({\frac {\mathbb {C} [t,x,y]}{(xy-t)}}\right)\to \mathbb {A} _{t}^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67063c8fec6b7b45dfe2f7670f3f5db7f1c01a1c)













