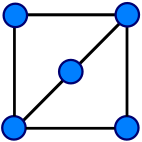
Homeomorphism (graph theory)
|
Read other articles:

Gavoi GavòiKomuneComune di GavoiLokasi Gavoi di Provinsi NuoroNegara ItaliaWilayah SardiniaProvinsiNuoro (NU)Pemerintahan • Wali kotaGiovanni CugusiLuas • Total38,06 km2 (14,70 sq mi)Ketinggian777 m (2,549 ft)Populasi (2016) • Total2,664[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos08020Kode area telepon0784Situs webhttp://www.comune.gavoi.nu.it Gavoi (bahasa Sardinia: Gavòi) adalah ...
Keuskupan Saint George's di GrenadaDioecesis Sancti GeorgiiKatolik Katedral Dikandung Tanpa NodaLokasiNegara GrenadaProvinsi gerejawiCastriesStatistikLuas340 km2 (130 sq mi)Populasi- Total- Katolik(per 2014)102.29546,485 (45.4%)Paroki20 (1 misi)Jemaat61[1]Imam7InformasiDenominasiKatolik RomaRitusRitus LatinPendirian20 Februari 1956 (68 tahun lalu)KatedralKatedral Dikandung Tanpa Noda, St. George'sPelindungBunda Maria[2]Kepemimpinan kiniPausFransiskusUsk...

Association football club in England Football clubRaynes Park ValeFull nameRaynes Park Vale Football ClubNickname(s)The ValeFounded1995GroundPrince George's Playing Fields, Grand Drive, Raynes ParkCapacity1,500ChairmanJohn DaltonManagerJosh GallagherLeagueIsthmian League South Central Division2022–23Combined Counties League Premier Division South, 1st of 20 (promoted)WebsiteClub website Home colours Away colours Raynes Park Vale Football Club is a semi-professional football club based in Ra...

Pour les articles homonymes, voir EMN. École nationale supérieure des mines de Nantes Mines NantesHistoireFondation 1990Dissolution 2017StatutType École d'ingénieurs (EPA)Directeur Robert Germinet (1990 - 2001)Stéphane Cassereau (2001 - 2012)Anne Beauval (2012 - 2016)Membre de Institut Mines-Télécom, Groupe des écoles des mines, CGE, Université Bretagne Loire, CDEFISite web www.mines-nantes.frChiffres-clésÉtudiants 1092[1]Enseignants-chercheurs 383[1]Budget 29,7 millions d'eurosLo...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. The End of the Certain World: The Life and Science of Max Born PengarangNancy Thorndike GreenspanNegaraAmerika SerikatBahasaInggrisSubjekSejarah fisikaMax BornPenerbitBasic BooksTanggal terbit2005Halaman374ISBNISBN 0-7382-0693-8OCLC56534998Desimal...

Further information: Cleveland Guardians Radio Network The Cleveland Guardians are currently heard on the radio via flagship stations WTAM (1100 AM/106.9 FM) and WMMS (100.7 FM),[1][2] with Tom Hamilton and Jim Rosenhaus comprising the announcing team.[3] Televised game coverage airs on Bally Sports Great Lakes, with select games simulcast over-the-air on WKYC (channel 3).[4] Matt Underwood handles television play-by-play duties, former Indian Rick Manning ser...

Isole Sparse dell'Oceano Indianodistretto[1]Îles Éparses de l'océan Indien (dettagli) (dettagli) Isole Sparse dell'Oceano Indiano – VedutaVeduta aerea di Europa LocalizzazioneStato Francia[1] Regione TAAF AmministrazionePresidente del Consiglio dipartimentaleprefetto delle TAAF[1]: Cécile Pozzo di Borgo capo distrettuale: Anne Tagand Data di istituzione21 febbraio 2007 TerritorioCoordinate22°20′38″S 40°22′02″E / 22.34388...

أحمد الأسعد معلومات شخصية اسم الولادة أحمد عبد اللطيف الأسعد الميلاد 1902 ميلاديالطيبة، قضاء مرجعيون، لبنان تاريخ الوفاة 1961 ميلادي الجنسية لبناني اللقب أبو كامل المذهب الفقهي شيعي الزوجة فاطمة كامل الأسعد (أم كامل) الأولاد كامل الأسعد - سعدى - زينب الحياة العملية التعلّ�...

Voce principale: Fußball-Club Würzburger Kickers. Fußball-Club Würzburger KickersStagione 2016-2017Sport calcio Squadra Kickers Würzburg Allenatore Bernd Hollerbach All. in seconda Lamine Cissé Peter Endres 2. Bundesliga17° Coppa di GermaniaSecondo turno Maggiori presenzeCampionato: Soriano (33)Totale: Soriano (35) Miglior marcatoreCampionato: Benatelli, Soriano (5)Totale: Soriano (6) Stadioflyeralarm Arena Maggior numero di spettatori13 080 vs St. Pauli (7 novembre 2016) Mi...

Halte Kertomenanggal Kertomenanggal Tampak luar Halte Kertomenanggal, 2020LokasiJalan Frontage Ahmad YaniMenanggal, Gayungan, Surabaya, Jawa Timur 60234IndonesiaKoordinat7°20′11″S 112°43′42″E / 7.33639°S 112.72833°E / -7.33639; 112.72833Koordinat: 7°20′11″S 112°43′42″E / 7.33639°S 112.72833°E / -7.33639; 112.72833Operator Kereta Api IndonesiaDaerah Operasi VIII Surabaya Letakkm 12+320 lintas Surabaya Kota-Probolinggo-Kali...

US home appliance brand CuisinartCompany typeSubsidiaryIndustryConsumer GoodsFounded1971; 53 years ago (1971)FounderCarl SontheimerHeadquartersStamford, Connecticut, U.S.ProductsCookware, ovenware, kitchen tools, kitchen accessoriesParentConair CorporationWebsitecuisinart.com Cuisinart (/ˈkwiːzɪnɑːrt/ kwee-zin-art) is an American kitchen appliance and cookware brand owned by Conair Corporation. Cuisinart was founded in 1971 by Carl Sontheimer and initially produced food...

Questa voce sugli argomenti attori statunitensi e doppiatori statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Dorian Harewood con Debbi Morgan Willie Dorian Harewood (Dayton, 6 agosto 1950) è un attore e doppiatore statunitense. Indice 1 Biografia 2 Filmografia parziale 2.1 Attore 2.1.1 Cinema 2.1.2 Televisione 2.2 Doppiatore 3 Doppiatori italiani 4 Altri progetti 5 Collegamenti esterni Bi...

American baseball player For the musician, see Paul Miner. Baseball player Paul MinnerPitcherBorn: (1923-07-30)July 30, 1923New Wilmington, Pennsylvania, U.S.Died: March 28, 2006(2006-03-28) (aged 82)Lemoyne, Pennsylvania, U.S.Batted: LeftThrew: LeftMLB debutSeptember 12, 1946, for the Brooklyn DodgersLast MLB appearanceJune 12, 1956, for the Chicago CubsMLB statisticsWin–loss record69–84Earned run average3.94Strikeouts481 Teams Brooklyn Dodgers (1946, 1...

Hungarian physicist The native form of this personal name is Eötvös Loránd. This article uses Western name order when mentioning individuals. Loránd EötvösEötvös in 1912Born27 July 1848Buda, Kingdom of HungaryDied8 April 1919(1919-04-08) (aged 70)Budapest, Hungarian Soviet RepublicNationalityHungarianAlma materUniversity of HeidelbergKnown forEötvös effect Eötvös experiment Eötvös number Eötvös ruleSpouseGizella HorvátChildrenJolán Rolanda IlonaParent(s)J�...
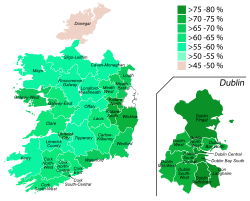
Amendemen Ketiga Puluh Enam Konstitusi Irlandia 2018Mengizinkan Oireachtas mengeluarkan undang-undang yang mengatur penghentian kehamilanLokasi IrlandiaTanggal25 Mei 2018 (2018-05-25) Hasil Suara % Ya 1.429.981 66,40% Tidak 723.632 33,60% Suara sah 2.153.613 99,72% Suara kosong atau tidak sah 6,042 0.28% Total suara 2,159,655 100.00% Pemilih terdaftar/hadir 3,367,556 64,13% Hasil menurut Daerah pilih Dáil Yes — No Sumber: referendum.ie Referendum aborsi Ir...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Arnon MilchanLahir6 Desember 1944 (umur 79)Rehovot, British Mandate of Palestine (sekarang Israel)KebangsaanIsraelPekerjaanPebisnisDikenal atasPendiri Regency EnterprisesKekayaan bersih US$3.7 miliar (oktober 4 2021)[1]Suami/istriBrigitte Genmaire (cerai)Amanda CoetzerAnak4[1] Arnon Milchan (Ibrani: ארנון מילצ'ן; lahir 6 Desember 1944) adalah pebisnis Israel yang telah memproduseri lebih dari 130 film.[2] Milchan, seorang miliarder dan pemilik ...

Hiu karang sirip hitam Carcharhinus melanopterus Rekaman dan Status konservasiRentanIUCN39375 TaksonomiKerajaanAnimaliaFilumChordataKelasChondrichthyesOrdoCarcharhiniformesFamiliCarcharhinidaeGenusCarcharhinusSpesiesCarcharhinus melanopterus Quoy dan Gaimard, 1824 Distribusi lbs Hiu karang sirip hitam (Carcharhinus melanopterus) merupakan salah satu jenis hiu yang termasuk dalam famili Carcharhinidae. Spesies ini dikenal dengan nama blacktip reef shark. Spesies hiu ini memiliki beberapa nama ...
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (septembre 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ?...

Arthouse movie theatre chain in the Los Angeles area Laemmle TheatresPlayhouse 7 in Pasadena, CaliforniaCompany typePrivateIndustryEntertainmentFounded1938; 86 years ago (1938)FounderMax and Kurt LaemmleArea servedLos Angeles, CaliforniaServicesMovie theater, Academy Award qualificationOwnerRobert and Greg LaemmleWebsitewww.laemmle.com Laemmle Theatres (/ˈlɛmli/ LEM-lee) is a group of family-run arthouse movie theaters in the Los Angeles area. It was established in 1938 ...