Alexandrov topology
|
Read other articles:
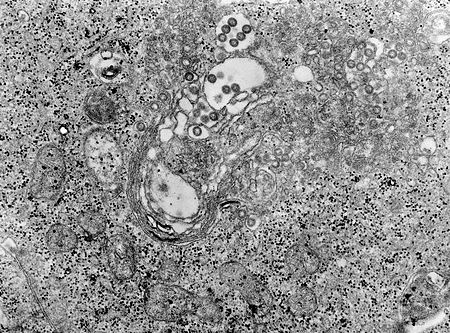
Demam lembah riftMikrograf TEM yang memaparkan keadaan jaringan tubuh yang dijangkiti virus Demam Rift ValleyInformasi umumSpesialisasiPenyakit infeksi, kedokteran hewan Virus Demam Rift Valley Klasifikasi virus Grup: Grup V ((−)ssRNA) Famili: Bunyaviridae Genus: Phlebovirus Spesies: Virus Demam Rift Valley Demam lembah rift (bahasa Inggris: rift valley fever, sering disingkat RVF) adalah penyakit yang terjadi akibat serangan virus RVF dari genus Phlebovirus, famili Phenuiviridae, dan...

Distrik Neihu distrik di Taiwan Tempat categoria:Articles mancats de coordenades Negara dengan pengakuan terbatasTaiwanKotaTaipei NegaraTaiwan Pembagian administratifXihu Village (en) Xikang Village (en) Xi'an Village (en) Gangqi Village (en) Gangdou Village (en) GangFu Village (en) Ganghua Village (en) Neihu Village (en) Hubin Village (en) Zixing Village (en) Dahu Village (en) Jinlong Village (en) Jinrui Village (en) Bishan Village (en) Ziyun Village (en) Qingbai Village (en) Huzhou Village ...
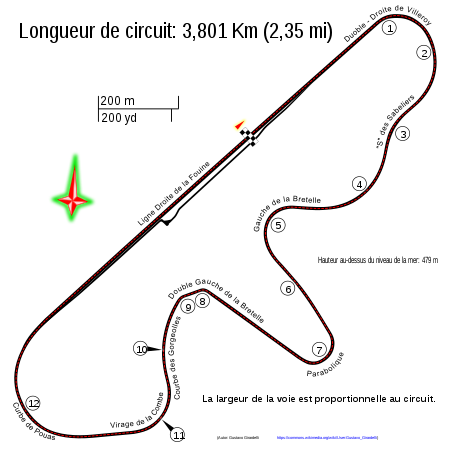
Circuit de Dijon-PrenoisLokasiDijon, FranceZona waktuGMT +1Acara besarFrench Grand Prix, Grand Prix de l'Age d'Or, Formula Renault 2.0 West European CupGrand Prix CircuitPanjang3.800 km (2.361 mi)Tikungan9Rekor lap1:02.985[1] (Ingo Gerstl, Toro Rosso STR1, 2015, BOSS GP Dijon Motors Cup)Short CircuitPanjang3.289 km (2.044 mi)Tikungan8 Dijon-Prenois adalah sirkuit balap sepanjang 3.801 km (2.362 mi) yang terletak di Prenois, dekat Dijon, Prancis. Trek bergelombang ini terkena...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Maurice Joyeux Naissance 29 janvier 1910Paris Décès 9 décembre 1991 (à 81 ans)Paris Première incarcération À l’âge de 14 ans, pour avoir cassé une côte au patron qui avait levé la main sur lui. Origine français Type de militance libraire écrivain essayiste action directe insoumis Cause défendue libertaire anarcho-syndicalisme modifier Le numéro 8 de la revue La Rue, en 1970. Maurice Joyeux, né le 29 janvier 1910 à Paris et mort le 9 décembre 1991 dans cette vil...

Serbian politician Nataša MićićНаташа МићићMićić in 2001President of SerbiaActingIn office29 December 2002 – 27 January 2004Prime MinisterZoran ĐinđićZoran ŽivkovićPreceded byMilan MilutinovićSucceeded byDragan Maršićanin (acting)President of the National Assembly of SerbiaIn office6 December 2001 – 27 January 2004Preceded byDragan MaršićaninSucceeded byDragan Maršićanin Personal detailsBorn (1965-11-02) 2 November 1965 (age 58)Titovo Už...

The library's logo, originally a 1906 bookplate[1] The Navy Department Library is the official library of the United States Department of the Navy. Located at the Washington Navy Yard in Washington, D.C., it is a part of the Naval History and Heritage Command. History On March 31, 1800, President John Adams wrote to Secretary of the Navy Benjamin Stoddert directing him to establish a library of the best writing...on the theory and practice of naval architecture, navigation, gunnery, h...

Best Day EverEpisode SpongeBob SquarePantsKartu judul episodeNomor episodeMusim 4Episode 80aSutradaraNate Cash (papan cerita)Tuck Tucker (papan cerita)Vincent Waller (kreatif)Larry Leichliter (animasi)PenulisNate CashTuck TuckerSteven BanksTanggal siar10 November 2006Kronologi episode ← SebelumnyaSquid Wood Selanjutnya →The Gift of Gum Daftar episode SpongeBob SquarePants Best Day Ever (Indonesia: Hari Terbaik yang Pernah Adacode: id is deprecated ) adalah episode musim ke-...

SalmtalstadionInformazioni generaliStato Germania UbicazioneSalmaue, Salmtal Inaugurazione1981 Ristrutturazione1986-1987 Informazioni tecnichePosti a sedere12000 Strutturapianta ellittica Coperturatribuna centrale Pista d’atleticapresente Mat. del terrenoErba Dim. del terreno105 x 68 m Uso e beneficiariCalcio FSV Salmrohr Mappa di localizzazione Modifica dati su Wikidata · ManualeCoordinate: 49°55′40.8″N 6°50′20.69″E / 49.928°N 6.83908°E49.928; 6....

Questa voce sull'argomento architetti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Thomas Ustick Walter Thomas Ustick Walter (Filadelfia, 4 settembre 1804 – Filadelfia, 30 ottobre 1882) è stato un architetto statunitense di origini tedesche. Di scuola neoclassica, tra i suoi primi lavori merita di essere ricordato il progetto per il Girard College di Filadelfia, realizzato a partire dagli anni trenta dell'Ottocento. Lavorò anche al...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: 628th Air Base Wing – news · newspapers · books · scholar · JSTOR (October 2011) (Learn how and when to remove this message) This article needs additiona...

PararunganDesaPeta lokasi Desa PararunganNegara IndonesiaProvinsiSumatera UtaraKabupatenTobaKecamatanHabinsaranKode pos22383Kode Kemendagri12.12.04.2024 Luas... km²Jumlah penduduk139 jiwa (2016)Kepadatan... jiwa/km² Pararungan adalah salah satu desa di Kecamatan Habinsaran, Kabupaten Toba, Provinsi Sumatera Utara, Indonesia. Desa Pararungan merupakan pemekaran desa Panamparan pada tahun 2010. Pemerintahan Kepala Desa Pararungan pada tahun 2021 adalah Purbauli Panjaitan.[1] Desa...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Guido VedovatoGuido Vedovato in his studioBorn (1961-06-30) June 30, 1961 (age 62)Vicenza, ItalyNationalityItalianKnown forPainting, Sculpture,MovementNaive art Guido Vedovato (30 June 1961 in Vicenza, Italy) Italian naïve painter and sculptor. Vedovato is one of the best-known Naïve artists. He was born in Vicenza, northern part of Italy. He lives and works in Camisano Vicentino. He graduated as an economist and had no artist scholar background. Yugoslavian Naïve art had a big e...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

ロリーナ・マッケニットLoreena McKennitt ロリーナ・マッケニット(2012年)基本情報出生名 Loreena Isabel Irene McKennitt生誕 1957年2月17日出身地 カナダ マニトバ州ジャンル ニューエイジ、ワールドミュージック、ケルト音楽職業 シンガーソングライター担当楽器 歌、ケルティック・ハープ、ピアノ、アコーディオン活動期間 1985年 -レーベル Quinlan Roadワーナー・ブラザース・レ...

Below is a list of members of the Order of the Companions of Honour from the order's creation in 1917 until the present day. Members Blue denotes honorary members. Yellow denotes living (ordinary) members. Pink denotes royal companions. Date Portrait Name Birth–Death Area of achievement 4 June 1917 Jan Smuts 1870–1950 Statesman 4 June 1917 Harry Gosling 1861–1930 Politician and trade unionist 4 June 1917 The Marchioness of Lansdowne 1850–1932 Court...

This article is about the town and tehsil of Uttar Pradesh. For district in Haryana, see Charkhi Dadri. For other uses, see Dadri (disambiguation). Not to be confused with Dardi. Town in Uttar Pradesh, IndiaDadriTownDadriLocation in Uttar Pradesh, IndiaShow map of Uttar PradeshDadriDadri (India)Show map of IndiaCoordinates: 28°33′00″N 77°33′11″E / 28.550°N 77.553°E / 28.550; 77.553CountryIndiaStateUttar PradeshDistrictGautam Buddha Nagar DistrictElevation21...

German javelin thrower Andreas HofmannHofmann at Bislett Games, 2016Personal informationFull nameAndreas Emil HofmannBorn (1991-12-16) 16 December 1991 (age 32)Heidelberg, GermanyEducationSchiller International University, Heidelberg campusHeight1.95 m (6 ft 5 in)Weight108 kg (238 lb)WebsiteHofmannAndreas.deSportCountry GermanySportTrack and fieldEventJavelin throwClubMTG MannheimCoached byLutz KlemmAchievements and titlesPersonal best92.06 m (2018) Med...

XX secolo · XXI secolo · XXII secolo Anni 2000 · Anni 2010 · Anni 2020 · Anni 2030 · Anni 2040 2018 · 2019 · 2020 · 2021 · 2022 · 2023 · 2024 · 2025 · 2026 Il 2022 (MMXXII in numeri romani) è un anno del XXI secolo. 2022 negli altri calendariCalendario gregoriano2022 Ab Urbe condita2775 (MMDCCLXXV) Calendario armeno1470 — 1471 Calendario bengalese1428 — 1429 Calendario berbero2972 Calendario...







