تكرار الوضعية ثلاثا
|
Read other articles:

Altun HaKuil Masonry AltarsLokasi di BelizeLokasiRockstone Pond, BelizeWilayahDistrik BelizeKoordinat17°45′50.22″N 88°20′49.42″W / 17.7639500°N 88.3470611°W / 17.7639500; -88.3470611SejarahDidirikan900 SMBudayaMayaCatatan situsTanggal ditemukan1961 Altun Ha /ɑːlˈtuːn hɑː/[1] adalah nama yang diberikan kepada reruntuhan sebuah kota Maya kuno di Belize, yang terletak di Distrik Belize. Tempat tersebut berjarak sekitar 50 kilomete...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 19 de enero de 2018. Diagrama 1. Apariencia del espacio-tiempo a lo largo de una línea de universo de un observador acelerado.La dirección vertical indica el tiempo, la horizontal indica la distancia espacial, la línea punteada es la trayectoria del observador en el espacio tiempo. El cuarto inferior representa el conjunto de sucesos pasados visibles al observador. Los punt...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Columbia University student organization Logo of the Columbia Queer Alliance Columbia Queer Alliance (CQA) is the central Columbia University student organization that represents lesbian, gay, bisexual, transgender, and questioning LGBTQ students. It is the oldest such student organization in the world, originally called the Student Homophile League, established in 1966[1] and recognized by the university on April 19, 1967.[2][3] History During its first year, the Stud...

Disambiguazione – Se stai cercando altri significati, vedi Manga (disambigua). I kanji per manga, tratti da Shiji no yukikai (1798) di Santō Kyōden e Kitao Shigemasa Manga (漫画? ascoltaⓘ) è un termine giapponese che indica i fumetti originari del Giappone. In Giappone invece il termine indica generalmente tutti i fumetti, indipendentemente dal target, dalle tematiche e dalla nazionalità di origine. A partire dagli anni cinquanta il manga è diventato uno dei settori principali...

Una certificazione verde COVID-19 in formato digitale sottoposta a scansione prima di entrare in un bistrò a Parma, in Italia. Un passaporto vaccinale o una prova di vaccinazione è un passaporto di immunità impiegato come credenziale[1] in paesi e giurisdizioni come parte degli sforzi per controllare la pandemia di COVID-19 tramite la vaccinazione. Un passaporto per il vaccino viene in genere rilasciato da un governo o da un'autorità sanitaria e di solito consiste in un documento ...

Seorang wanita belanja-jendela Belanja-jendela, terkadang disebut lihat-lihat saja, mengacu pada aktivitas di mana konsumen menelusuri atau memeriksa barang dagangan toko sebagai bentuk waktu luang atau perilaku pencarian eksternal tanpa niat untuk membeli saat ini. Bergantung pada individu, belanja-jendela bisa menjadi hobi atau digunakan untuk mendapatkan informasi tentang perkembangan produk, perbedaan merek, atau harga jual.[1] Perkembangan belanja-jendela sebagai bentuk rekreasi ...

I-22 Sikatan Mockup dari I-22 Sikatan di pameran Indo Defense Expo & Forum yang digelar di JlExpo Kemayoran pada 2-5 November 2022 Jenis Pesawat tempur multiperan siluman Negara asal Indonesia Pembuat PT. Infoglobal Teknologi Semesta Penerbangan perdana Tidak diketahui Status Dalam pengembangan Pengguna utama TNI Infoglobal I-22 Sikatan adalah program pengembangan pesawat tempur multiperan generasi 4,5 Indonesia yang dilakukan oleh PT. Infoglobal Teknologi Semesta.[1] Pesawa...

Order MahkotaPerwira Orde Mahkota BelgiaDianugerahkan oleh Kerajaan BelgiaTipeOrde kekesatriaan dengan lima kelas, dua palem, dan tiga medaliDibentuk15 Oktober 18971897 - 1908 (sebagai tanda kehormatan Kongo)1908 - sekarang (sebagai tanda kehormatan Belgia)MottoTRAVAIL ET PROGRES -ARBEID EN VOORUITGANGKelayakanOrang yang berumur di atas 42 tahunDianugerahkan kepadaPengabdian berjasa bagi negara BelgiaStatusMasih dianugerahkanPemilik AgungYang Mulia Raja PhilippeTingkatSalib BesarPerwira...

GayamsariKecamatanPeta lokasi Kecamatan GayamsariNegara IndonesiaProvinsiJawa TengahKotaSemarangPemerintahan • CamatEKO YUNIARTO S.IP MMPopulasi • Total69 33.400 jiwa (2.022) jiwaKode Kemendagri33.74.04 Kode BPS3374100 Luas6,22 km² Gayamsari (bahasa Jawa: ꦒꦪꦩ꧀ꦱꦫꦶ) adalah sebuah kecamatan di Kota Semarang, Provinsi Jawa Tengah, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemu...

Artikel ini adalah bagian dari seri:Sejarah permainan video Umum Masa keemasan permainan video arcade Sejarah permainan video Kelesuan permainan video di Amerika Utara 1983 Konsol Generasi pertama (1972–1977) Generasi kedua (1976–1984) Generasi ketiga (1983–1992) Generasi keempat (1987–1996) Generasi kelima (1993–2006) Generasi keenam (1998–) Generasi ketujuh (2005–) Generasi kedelapan (2012–) Ragam Sejarah permainan peran daring multipemain masif Sejarah permainan daring Seja...

Computer security This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2021) Security information and event management (SIEM) is a field within the field of computer security, where software products and services combine security information management (SIM) and security event management (SEM).[1][2] SIEM is the core component of...

Vous lisez un « bon article » labellisé en 2017. Diagramme de Feynman : un électron et un positron (e- et e+) s'annihilent en produisant un photon virtuel (en bleu) qui devient une paire quark-antiquark (q et q̄), puis l'antiquark émet un gluon (en vert). Le temps est ici en abscisse, de gauche à droite ; l'espace est en ordonnée.Les flèches symbolisent le type de l'objet (particules >, vers le futur, et antiparticules <) et non un sens de déplacement ...

Tambang kapur yang dikenal dengan nama Bukit Jaddih di Desa Jaddih, Kecamatan Socah, Kabupaten Bangkalan, Jawa Timur The Needles, terletak di Isle of Wight, adalah bagian dari Southern England Chalk Formation. Pabrik kapur di Tagogapu, Padalarang, Bandung Barat pada tahun 1920-an Kapur adalah material yang berasal dari batuan sedimen berwarna putih dan halus yang terutama tersusun dari mineral kalsium. Tiga senyawa utama yang mewujudkan kapur adalah kalsium karbonat (mendominasi gamping dan k...

1959 American film by John Ford For the 2018 film, see Horse Soldiers (film). For the 2009 book Horse Soldiers, about soldiers in Afghanistan, see Doug Stanton. The Horse Soldiers1959 movie posterDirected byJohn FordScreenplay byJohn Lee MahinMartin RackinBased onThe Horse Soldiers1956 novelby Harold SinclairProduced byJohn Lee Mahin (uncredited)Martin Rackin (uncredited)Allen K. Wood (production manager)[1]StarringJohn WayneWilliam HoldenConstance TowersCinematographyWilliam H. Cloth...
A type of boxing practiced in the Chivarreto villa in San Francisco El Alto, Totonicapan, Guatemala Chivarreto boxing, also known as Boxeo a puño limpio, is a type of boxing that is practiced in the Chivarreto villa in San Francisco El Alto, Totonicapan, Guatemala. It is a popular activity in town and there is an annual tournament, held during Semana Santa every year, with fights held on Good Friday.[1] The tournaments began as a punishment to criminals who'd then have to fight it ou...
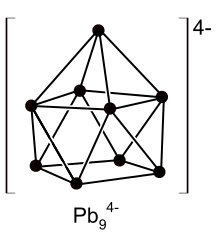
Struttura dello ione di Zintl Pb94- Eduard Zintl (Weiden in der Oberpfalz, 21 gennaio 1898 – Darmstadt, 17 gennaio 1941) è stato un chimico tedesco, maggiormente noto per i suoi studi su alcuni composti intermetallici che, in suo onore, furono definiti fasi di Zintl e per la scoperta dei polianioni metallici formati da alcuni elementi chimici, chiamati ioni di Zintl. Terminati gli studi a Monaco, dove si trasferì con la sua famiglia, all'età di diciotto anni, Zintl venne arruolato per co...

First Lady of the Republic of China中华民国第一配偶IncumbentWu Mei-jusince 20 May 2024Inaugural holderLu Muzhen (1912)Soong Mei-ling (1949)Formation1 January 1912 The first lady of the Republic of China (Chinese: 中华民国第一配偶; pinyin: Zhōnghuá mínguó dì yī pèi'ǒu) refers to the wife of the President of the Republic of China.[1] Since 1949, the position has been based in Taiwan, where they are often called by the title of first lady of Taiwan,&...

Dutch psycholinguist You can help expand this article with text translated from the corresponding article in German. (January 2013) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text in...

The List of Kuruluş: Osman characters lists the characters appearing in Kuruluş: Osman, a Turkish TV series created by Mehmet Bozdağ.[1] It focused on the life of Osman I, founder of the Ottoman Empire.[1] Osman is portrayed by Burak Özçivit.[2] Most of the characters are based on people related to Osman I, including Malhun Hatun, Rabia Bala Hatun, Orhan, Sheikh Edebali, Ertuğrul and Köse Mihal along with fictional characters adapted from the Book of Dede Korku...
