Kerajaan konstitusional
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Three-star general of the Pakistan Army Lieutenant GeneralWaheed ArshadBirth nameWaheed ArshadAllegiance PakistanService/branch Pakistan ArmyYears of service1975 - 2013Rank Lieutenant GeneralUnitPakistan Army Armoured CorpsCommands heldChief of General Staff (CGS)IG Training and Evaluation (IGT&E)Vice Chief of General Staff (VCGS)DG Planning at COAS SecretariatDirector General ISPRCommander 26th Mechanized DivisionBattles/warsIndo-Pakistani War of 1999War in North West-Paki...

American politician Lowndes H. DavisIllustration from 1882's Public Men of To-DayMember of the U.S. House of Representativesfrom MissouriIn officeMarch 4, 1879 – March 3, 1885Preceded byRobert Anthony HatcherSucceeded byWilliam DawsonConstituency4th district (1879–1883)14th district (1883–1885) Personal detailsBornLowndes Henry Davis(1836-12-13)December 13, 1836Jackson, Missouri, U.S.DiedFebruary 4, 1920(1920-02-04) (aged 83)Cape Girardeau, Missouri, U.S.Restin...

تيرول إنسبروك الاسم الكامل نادي تيرول إنسبروك لكرة القدم تأسس عام 1993 انحل عام 2002 الملعب ملعب تيفولي الجديد(السعة: 17,200) البلد النمسا الدوري الدوري النمساوي الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل نادي تيرول إنسبروك لكرة القدم كان نادي كرة قدم في النمسا تأس�...

Плотность населения Аляски Население Аляски Год Численность Изменение 1880 33 426 - 1890 32 052 -4.1 % 1900 63 592 98,4 % 1910 64 356 1,2 % 1920 55 036 -14,5 % 1930 59 278 7,7 % 1940 72 524 22,3 % 1950 128 643 77,4 % 1960 226 167 75.8 % 1970 300 382 32,8 % 1980 401 851 33,8 % 1990 550 043 36,9 % 2000 626 932 14,0 % 2010 710 231 13,3 % 2020 736 081 3,6 % Аляс�...

Gempa bumi Taiwan 2016Waktu UTC2016-02-05 19:57:27ISC611838796USGS-ANSSComCatTanggal setempat06 Februari 2016 (2016-02-06)Waktu setempat03:57:27 (UTC+8)Kekuatan6.4 MwKedalaman23,0 km (14,3 mi)EpisentrumKaohsiung, TaiwanWilayah bencana Republik Tiongkok (Taiwan)Intensitas maks.VII (Sangat kuat)CWB 5− Korban116 korban meninggal 437 luka-luka[1] Pada pukul 3.57 waktu setempat (19.57 UTC) pada tanggal 6 Februari 2016, gempa bumi dengan skala kekuatan m...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Alessandro Banfi Nazionalità Italia Calcio Ruolo Terzino Carriera Squadre di club1 1930-1932 Monza11 (0)1932-1933 Comense17 (0)1933-1938 Monza123 (6)1938-1943 Como119 (1)1945-1946 Casatese? (?) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campio...

Ini adalah nama Korea; marganya adalah Park. Park Soo-hongLahir27 Oktober 1970 (umur 53)Seoul, Korea SelatanMediaStand-up, televisiKebangsaanKorea SelatanTahun aktif2002–sekarangGenreObservasional, Sketsa, Wit, Parodi, Slapstick, Drama, SitkomNama KoreaHangul박수홍 Hanja朴修弘 Alih AksaraBak Su-hongMcCune–ReischauerPak Su-hong Park Soo-hong (lahir 27 Oktober 1970), adalah seorang komedian dan presenter asal Korea Selatan.[1] Biografi Park Soo-hong lahir di Seoul pada 27...

2019 South Korean television series Beautiful Love, Wonderful LifePromotional posterHangul사랑은 뷰티풀 인생은 원더풀Literal meaningLove Is Beautiful, Life Is WonderfulRevised RomanizationSarang-eun Byutipul Insaeng-eun Wondeopul GenreMelodramaRomantic comedyCreated byKBS Drama ProductionWritten byBae Yoo-MiDirected byHan Joon-SeoStarringSeol In-ahKim Jae-youngJo Yoon-heeYoon ParkOh Min-sukComposerChoi In HeeCountry of originSouth KoreaOriginal languageKoreanNo. of episodes100[...

Racket sport SquashA squash player prepares to strike the ball with his racketHighest governing bodyWorld Squash Federation (WSF)First played19th century, England, United KingdomCharacteristicsContactLimitedTeam membersSingles or doublesMixed-sexSeparate competitions (mixed sometimes in leagues)TypeRacket sportEquipmentSquash ball, squash racket, goggles, non-marking gum soled shoesVenueIndoor or outdoor (with glass court)PresenceOlympicTo be included in 2028World Games1997, 2005–prese...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...

Tanjong Dawai redirects here. For the state constituency, see Tanjong Dawai (state constituency). This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tanjung Dawai – news · newspapers · books · scholar · JSTOR (February 2016) (Learn how and when to remove this message) Tanjung Dawai in Kuala Muda District Tanjung Dawai is a small...

Liverpool Rifles6th Bn (Rifles) King's Regiment38th (King's) Searchlight Regiment, RA635 (King's Regiment) Regiment, RA573 (King's Regiment) HAA Regiment, RAActiveFrom 19 August 1859Country United KingdomBranch Territorial ForceRoleInfantry, searchlight, artilleryPart ofKing's Regiment (Liverpool)Garrison/HQPrinces Park Barracks, LiverpoolEngagementsWestern FrontThe BlitzOperation DiverOperation DoomsdayBattle honoursSouth Africa 1900–01Military unit The Liverpool Rifles was...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Joanne MissinghamCina黑嘉嘉Lahir26 Mei 1994 (umur 30)Brisbane, AustraliaKediaman Amerika SerikatGuruZhou Keping Lin Shengxian Ruan Yunsheng Wu KaiTurned pro2008Peringkat7 danAfiliasiTaiwan Qiyuan Joanne Missingham Hanzi: 黑嘉嘉 Alih aksara ...

Зіньків Герб Зінькова Прапор Зінькова У центрі Зінькова — вулиця Воздвиженська, жовтень 2010 року Основні дані Країна Україна Область Полтавська область Район Полтавський район Громада Зіньківська міська громада Код КОАТУУ: 5321310100 Засноване 1604 Статус міста з 1604 року �...

Bangladeshi politician Anisul Islam Mahmudআনিসুল ইসলাম মাহমুদMahmud in 2015Member of ParliamentIncumbentAssumed office 29 December 2008Preceded bySyed Wahidul AlamConstituencyChittagong-5In office2 April 1979 – 6 December 1990Preceded byAbdul WahabSucceeded bySyed Wahidul AlamConstituencyChittagong-5Minister of Environment and ForestIn office3 January 2018 – 6 January 2019Prime MinisterSheikh HasinaPreceded byAnwar Hossain ManjuSucce...

Peste neraepidemiaTrionfo della morte, 1446, Palazzo Sclafani, Galleria regionale di Palazzo Abatellis, Palermo, affresco staccatoPatologiaDiffusione tramite i roditori, scarsa igiene, guerre, epidemie minori LuogoAsia, Europa, Nordafrica, Caucaso Nazioni coinvolteGeorgia, Azerbaigian, Russia e Armenia Periodo1346 -1353 Dati statistici globali[1]Numero di morticirca 20 milioni di vittime stimate in Europa[2] Modifica dati su Wikidata · Manuale La peste nera fu ...

High school in Oregon Colton High SchoolAddress30205 Wall StreetColton, Clackamas County, Oregon 97017United StatesCoordinates45°10′15″N 122°26′18″W / 45.170732°N 122.438325°W / 45.170732; -122.438325InformationTypePublicSchool districtColton School DistrictPrincipalTravis Remmick [1]Grades9-12Number of students199 (2016-17)[2]Color(s)Green and gold [3]Athletics conferenceOSAA Tri-River 2A-2[3]MascotVikings[3&...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Puerto Rico (Begriffsklärung) aufgeführt. Freistaat Puerto Rico Estado Libre Asociado de Puerto Rico (spanisch)Commonwealth of Puerto Rico (englisch) Flagge Wappen Wahlspruch: Ioannes Est Nomen Eius(lateinisch für Johannes ist sein Name) Amtssprache Spanisch und Englisch Hauptstadt San Juan Staats- und Regierungsform Nichtinkorporiertes US-amerikanisches Außengebiet Staatsoberhaupt Präsident Joe Biden Regierungsche...

Targa-ricordo di Krejn per Wikipedia, opera di Sergej Marčenko Premio Wolf per la matematica 1982 Mark Grigor'evič Krejn (in russo Марк Григорьевич Крейн?; in ucraino Марко Григорович Крейн?, Marko Grigorovyč Krejn; Kiev, 3 aprile 1907 – Odessa, 17 ottobre 1989) è stato un matematico sovietico, considerato uno dei maggiori esponenti della scuola sovietica di analisi funzionale. È conosciuto per il suo lavoro nella teoria degli operatori...
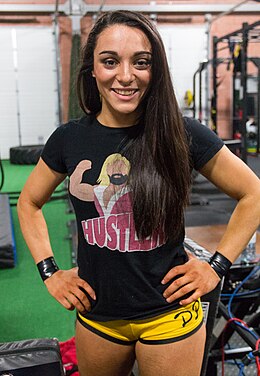
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article concernant le catch doit être recyclé (juillet 2021). Une réorganisation et une clarification du contenu paraissent nécessaires. Améliorez-le, discutez des points à améliorer ou précisez les sections à recycler en utilisant {{section à recycler}}. Deonna PurrazzoDeonna Purrazzo en 2016Données généralesNom de naissance Deonna Lynn PurrazzoNom de ring Deonna Purrazzo [1] DeonnaNationalité ...