Elektrodinamika kuantum
|
Read other articles:

Bible House, kantor pusat Pennsylvania Bible Society, lembaga Alkitab tertua di Amerika Serikat, didirikan pada tahun 1808 Lembaga Alkitab (Inggris: Bible Societycode: en is deprecated ) adalah suatu organisasi nirlaba, biasanya berupa yayasan ekumenikal, berfokus pada penerjemahan, penerbitan, dan distribusi Alkitab dengan biaya terjangkau. Dalam tahun-tahun terakhir mereka juga lebih terlibat dalam advokasi kredibilitas dan dapat dipercayanya Alkitab dalam kehidupan budaya kontemporer. Seca...

Penggambaran Bodawpaya di Istana Amarapura pada tahun 1795 Bodawpaya adalah salah satu raja terbesar Myanmar.[1] Ia merupakan raja keenam dari dinasti Alaungpaya.[1][2] Pada tahun 1784 Bodawpaya menginvasi Rakhine, kerajaan maritim di pantai timur Teluk Benggala.[1] Pada invasi tersebut ia menangkap Raja Thamada dan mendeportasi lebih dari 20.000 orang ke Myanmar sebagai budak.[1][2] Keberhasilan dalam menangkap Raja Thamada menuntunnya untuk me...

Not to be confused with The League of Extraordinary Gentlemen. 2006 filmA League of Ordinary GentlemenDirected byChristopher Browne and Alex BrowneWritten byChristopher BrowneProduced byChristopher BrowneStarringWayne WebbPete WeberWalter Ray Williams Jr.Chris BarnesSteve MillerCinematographyKen SengEdited byKurt EngfehrDavid S. TungMusic byGary MeisterDistributed byMagnolia Home EntertainmentRelease dateMarch 21, 2006Running time93 min.LanguageEnglish A League of Ordinary Gentlemen is a docu...

Voce principale: Promozione 1969-1970. Promozione Lombardia 1969-1970 Competizione Promozione Sport Calcio Edizione 14ª Organizzatore FIGC - LNDComitato Regionale Lombardo Luogo Italia Cronologia della competizione 1968-1969 1970-1971 Manuale Nella stagione 1969-1970 la Promozione era il quinto livello del calcio italiano (il massimo livello regionale). Qui vi sono le statistiche relative al campionato in Lombardia. Il campionato di Promozione Lombarda 1969-70 è stato il 14º campion...

JogonalanKecamatanPeta lokasi Kecamatan JogonalanNegara IndonesiaProvinsiJawa TengahKabupatenKlatenPemerintahan • CamatMurdoko,SH.Populasi • Total58,526 jiwaKode Kemendagri33.10.08 Kode BPS3310090 Luas26,70 km²Desa/kelurahan18 Jogonalan (Jawa: ꦗꦒꦤꦭꦤ꧀, translit. Jaganalan) adalah sebuah kecamatan di Kabupaten Klaten, Jawa Tengah Batas Wilayah Utara Kecamatan Karangnongko Timur laut Kecamatan Kebonarum Timur Kecamatan Klaten Selatan Tenggara Ke...

Part of a banquet in Greek and Etruscan art This article is about the social custom in ancient Greece. For other uses, see Symposium (disambiguation). A symposium scene on a fresco in the Tomb of the Diver from the Greek colony of Paestum, in Italy, 480–470 BC A female aulos-player entertains men at a symposium on this Attic red-figure bell-krater, c. 420 BC. In Ancient Greece, the symposium (Greek: συμπόσιον, sympósion or symposio, from συμπίνειν, sympínein, to dr...
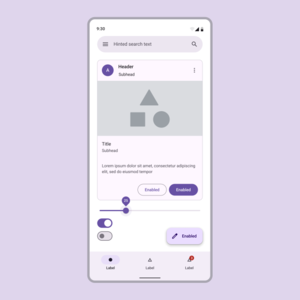
Material Design Tipedesign language, perangkat lunak dan JavaScript library Versi pertama25 Juni 2014; 9 tahun lalu (2014-06-25)Versi stabilDaftariOS, GitHub: 124.2.0 (26 April 2021)peramban web: 14.0.0 (28 April 2022)Android: 1.11.0 (14 Desember 2023) Versi sebelumnya Android: 1.8.0-rc01 (6 Januari 2023) GenreSistem desain perangkat lunakLisensi Android, iOS: Apache-2.0 License Flutter: BSD-3-Clause License Web: MIT license Karakteristik teknisSistem operasiLintas platform PlatformAndro...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2015) (Learn how and when to remove this message) Membership in registered non-Christian religious organizations in Iceland. The dark blue line represents Buddhism Buddhism in Iceland is followed by 0.43% of the population of Iceland, according to the 2021 Census.[1...

1793–1921 unit of Russia Minsk GovernorateМинская губернияGovernorate of the Russian Empire1793–1921 Coat of arms Location in the Russian EmpireCapitalMinskArea • 91,213 km2 (35,218 sq mi)Population • 2,539,100 History • Established 23 March 1793• Disestablished 1921 Preceded by Succeeded by Minsk Voivodeship Minsk Okrug Slutsk Okrug Bobruysk Okrug Polissia Okruha Borisov Okrug Gomel Governorate Polesie Voivodeship ...

American astronaut and lunar explorer (1930–2012) For other uses, see Neil Armstrong (disambiguation). Neil ArmstrongArmstrong in 1969BornNeil Alden Armstrong(1930-08-05)August 5, 1930Wapakoneta, Ohio, U.S.DiedAugust 25, 2012(2012-08-25) (aged 82)Fairfield, Ohio, U.S.EducationPurdue University (BS)University of Southern California (MS)Spouses Janet Shearon (m. 1956; div. 1994) Carol Knight (m. 1994) Chil...

Step bt Stepsingolo discograficoScreenshot tratto dal video del branoArtistaWhitney Houston Pubblicazione24 febbraio 1997 Durata4:12 Album di provenienzaColonna sonora di Uno sguardo dal cielo GenereContemporary R&BPop EtichettaArista Records ProduttoreStephen Lipson Registrazione1996 FormatiCD CertificazioniDischi d'oro Germania[1](vendite: 250 000+) Whitney Houston - cronologiaSingolo precedenteI Believe in You and Me(1996)Singolo successivoMy Heart Is Calling(199...

لمعانٍ أخرى، طالع ساحل الذهب (توضيح). ساحل الذهب Akans (إمبراطورية آشانتي) دنماركيون (ساحل الذهب الدنماركي) هولنديون (الشاطئ الهولندي الذهبي) بريطانيون (ساحل الذهب الإنجليزي) ألمان (براندبورغ ساحل الذهب, براندبورغ ساحل الذهب) برتغاليون (ساحل الذهب البرتغالي) سويديون (ساح...

Military operation attacking from air and sea to land Amphibious assault redirects here. For the band Amphibious Assault, see Fallon Bowman. A Crusader tank landing on a beach from a Tank Landing Craft in a 1942 test Part of a series onWarOutline History Prehistoric Ancient Post-classical castles Early modern pike and shot napoleonic Late modern industrial fourth-gen Military Organization Command and control Defense ministry Army Navy Air force Marines Coast guard Space force Reserves Regula...

J1 League 20212021 Meiji Yasuda J1 League Competizione J1 League Sport Calcio Edizione 29ª Organizzatore J1 League Date dal 26 febbraio 2021al 4 dicembre 2021 Luogo Giappone Partecipanti 20 Formula Girone all'italiana Risultati Vincitore Kawasaki Frontale(4º titolo) Retrocessioni Tokushima VortisOita TrinitaVegalta SendaiYokohama FC Statistiche Miglior marcatore Daizen Maeda Leandro Damião (23) Incontri disputati 380 Gol segnati 881 (2,32 per incontro) Cronologia d...

Río Misisipi(Mississippi River) El río Misisipi en su confluencia con el río Misuri, al sur de San Luis (Misuri)Ubicación geográficaCuenca Río MisisipiNacimiento Lago Itasca (Minesota)Desembocadura Golfo de MéxicoCoordenadas 47°14′23″N 95°12′27″O / 47.2397, -95.2075Ubicación administrativaPaís Estados UnidosDivisión Minnesota Wisconsin Iowa Misuri Illinois Kentucky Tennessee Arkansas Misisipi ...

Head of state and of government of the United Republic of Tanzania President of the United Republic of TanzaniaRais wa Jamhuri ya Muungano wa TanzaniaCoat of arms of TanzaniaPresidential StandardIncumbentSamia Suluhu Hassansince 19 March 2021Executive branch of the Government of TanzaniaStyleHer ExcellencyMheshimiwa Rais (Swahili)TypeHead of stateHead of governmentMember ofCabinetResidenceIkuluSeatDodomaTerm lengthFive years, renewable onceConstituting instrument1977 ConstitutionFor...

Logo der US-DEU um 2004 Unie svobody – Demokratická unie (US-DEU, deutsch Freiheitsunion – Demokratische Union) war eine liberal-konservative Partei in Tschechien.[1] Die Unie svobody entstand 1998 als Abspaltung von der ODS. Sie fusionierte 2001 mit der außerparlamentarischen Demokratická unie. Von 2002 bis 2006 war die US-DEU als Juniorpartner an der Regierung beteiligt. Ab 2006 war sie nicht mehr im Parlament vertreten, 2011 löste sie sich auf. Inhaltsverzeichnis 1 Ausricht...

إليوشن إل-96إيروفلوت أل-96-300معلومات عامةالنوع طائرة نفاثةبلد الأصل روسياسعر الوحدة 40 إلى 50 مليون دولار أمريكيالتطوير والتصنيعالصانع فورونيج لصناعة الطائراتالمصمم إليوشنسنة الصنع 1993 إلى الأنالكمية المصنوعة 29 وحدةطورت من إليوشن إل-86سيرة الطائرةدخول الخدمة 29 ديسمبر 1992 مع إ...

هيلغيرت شعار الإحداثيات 50°27′21″N 7°41′20″E / 50.455833333333°N 7.6888888888889°E / 50.455833333333; 7.6888888888889 [1] تقسيم إداري البلد ألمانيا[2][3] التقسيم الأعلى منطقة فيستر فالد كرآيس خصائص جغرافية المساحة 4.57 كيلومتر مربع (31 ديسمبر 2017)[4] ارتف...


