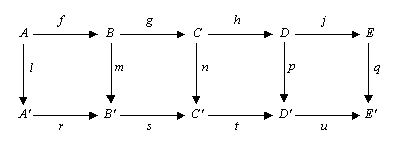
Aljabar homologis
|
Read other articles:

Untuk filologis Jerman, lihat Johann Christoph Wilhelm Ludwig Döderlein. Ludwig Heinrich Philipp DöderleinLahir(1855-03-03)3 Maret 1855Bad Bergzabern, Kerajaan Bayern, Konfederasi JermanMeninggal23 April 1936(1936-04-23) (umur 81)Munich, JermanKebangsaanJermanAlmamater Universitas Erlangen-Nuremberg Universitas Ludwig Maximilian Munich Universitas Strasbourg Karier ilmiahBidangZoologiInstitusi Universitas Tokyo Musée zoologique de la ville de Strasbourg Zoologische Staatssammlung Mün...

Ini adalah nama Korea; marganya adalah Moon. Moon Jae-in문재인Moon Jae-in pada tahun 2017 Presiden Korea Selatan ke-12Masa jabatan10 Mei 2017 – 10 Mei 2022Perdana MenteriHwang Kyo-ahnYoo Il-ho (Pelaksana tugas)Lee Nak-yeon PendahuluPark Geun-hyeHwang Kyo-ahn (Pelaksana tugas)PenggantiYoon Seok-yeolPemimpin Partai MinjooMasa jabatan9 Februari 2015 – 27 Januari 2016 PendahuluAhn Cheol-sooKim Han-gilPenggantiKim Chong-inAnggota Majelis Nasionaluntuk SasangMasa jabatan30 ...

Radio Inter DadesTipusemissora de ràdio HistòriaCreació12 de febrer de 1950 Radio Inter o La Inter, anteriorment coneguda com a Radio Intercontinental, és una emissora de ràdio espanyola de caràcter generalista, amb emissió en diferents freqüències en l'FM i en Internet. Pertany a la societat anònima Companyia de Radiodifusió Intercontinental (CRISA), propietat al 96,7% del Grup Intereconomía. Els seus estudis es troben al Carrer Modesto Lafuente 42 de Madrid. Des del 7 de gener 2...
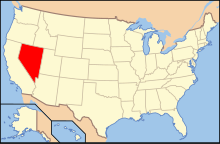
LGBT rights in NevadaNevada (USA)StatusLegal since 1993, age of consent equal since 2013Gender identityState does not require surgery to change gender on birth certificateDiscrimination protectionsSexual orientation and gender identity or expression (see below)Family rightsRecognition of relationshipsDomestic partnerships legal since 2009;Same-sex marriage since 2014AdoptionSame-sex couples allowed to adopt Lesbian, gay, bisexual, and transgender (LGBT) people in the U.S. state of Nevada enj...

LGBT rights in PortugalLocation of Portugal (dark green)– in Europe (light green & dark grey)– in the European Union (light green) – [Legend]StatusLegal since 1982;age of consent equalized in 2007MilitaryGays, lesbians and bisexuals allowed to serve openlyDiscrimination protectionsSexual orientation and gender identity protections (see below)Family rightsRecognition of relationshipsDe facto union since 2001,Same-sex marriage si...

Freshwater aquarium Lists of aquarium life include lists of fish, amphibians, invertebrates and plants in freshwater, brackish and marine aquariums. In fishkeeping, suitable species of aquarium fish, plants and other organisms vary with the size, water chemistry and temperature of the aquarium. The lists include: List of brackish aquarium fish species List of freshwater aquarium amphibian species List of freshwater aquarium fish species List of freshwater aquarium invertebrate species List o...

Ente nazionale per l'aviazione civile ENAC sede principale di Roma SiglaENAC Stato Italia TipoEnte pubblico Istituito25 luglio 1997 daGoverno Prodi I PredecessoreRegistro aeronautico italiano (RAI), Ente nazionale gente dell'aria (ENGA), Direzione generale dell'aviazione civile (Civilavia) PresidentePierluigi Di Palma Direttore generaleAlessio Quaranta Bilancio210,3 milioni di euro (2015)[1] Impiegati838[2] Sedeviale Castro Pretorio, 11800185 Roma via Gaeta, 300185 Roma v...

Overview of and topical guide to ancient Egypt The Great Sphinx of Giza and Khafre Pyramid The following outline is provided as an overview of a topical guide to ancient Egypt: Ancient Egypt – ancient civilization of eastern North Africa, concentrated along the lower reaches of the Nile River in what is now the modern country of Egypt. Egyptian civilization coalesced around 3150 BCE (according to conventional Egyptian chronology)[1] with the political unification of Upper a...

Cosby indagaTitolo di testa della serie televisivaTitolo originaleThe Cosby Mysteries PaeseStati Uniti d'America Anno1994-1995 Formatoserie TV Generepoliziesco, commedia Stagioni1 Episodi18 Durata60 min (episodio) Lingua originaleinglese CreditiIdeatoreDavid Black, William Link Interpreti e personaggi Bill Cosby: Guy Hanks James Naughton: il detective Adam Sully Robert Stanton: il medico legale John Chapman Rita Moreno: Angie Corea Mos Def: Dante Lynn Whitfield: Barbara Lorenz Doppiatori ...

Jan van Leyden redirects here. For another person, see Jan van Leyden (painter). Dutch Anabaptist leader (1509–1536) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2015) (Learn how and when to remove this message) John of LeidenAnabaptist King of Münster self-proclaimed Reign8 September 1534 – 24 June 1535 (1534-09...

المسجد الحرام من أقدس المساجد عند المسلمين دار العبادة (ج. دور العبادة) هو مبنى أو مساحة مخصصة لأداء العبادة، حيث يأتي شخص أو مجموعة من الأشخاص لأداء طقس أو طقوس دينية.[1][2] مراجع ^ The New Testament Definition of the Church. مؤرشف من الأصل في 2016-01-24. اطلع عليه بتاريخ 2009-06-23. ^ Gee، Matthew (8 مايو ...

1969 studio album by Harry NilssonHarryStudio album by Harry NilssonReleasedAugust 1969GenrePopLength40:57LabelRCA VictorProducerHarry Nilsson, Rick JarrardHarry Nilsson chronology Skidoo (soundtrack)(1968) Harry(1969) Nilsson Sings Newman(1970) Singles from Harry Rainmaker / I Will Take You ThereReleased: November 1968 Maybe / Marchin' Down BroadwayReleased: July 1969 Maybe / I Guess the Lord Must Be in New York CityReleased: September 1969 Professional ratingsReview scoresSourceRati...

1918 client state of the German Empire This article is about the client state that existed in 1918. For the Cossack State of the 17th–18th centuries, see Cossack Hetmanate. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ukrainian State – news · newspapers · books · scholar · JSTOR (December 2022) (Learn h...

American mathematical physicist (1910–1994) Charles CritchfieldCritchfield's Los Alamos ID badge photoBornJune 7, 1910Shreve, Ohio, USDiedFebruary 12, 1994 (aged 83)Los Alamos, New Mexico, USEducationGeorge Washington University (BS, MS, PhD)Known forNuclear weaponsManhattan ProjectBalloon technologyScientific careerFieldsMathematical PhysicsInstitutionsInstitute for Advanced StudyHarvard UniversityCarnegie InstitutionLos Alamos National LaboratoryUniversity of MinnesotaDoctoral adviso...

Jamaal BowmanJamaal Bowman Membro della Camera dei Rappresentanti - New York, distretto n.16Durata mandato3 gennaio 2021 - In carica PredecessoreEliot Engel Dati generaliPartito politicoDemocratico Jamaal Bowman (New York, 1º aprile 1976) è un politico statunitense[1], membro della Camera dei Rappresentanti per lo stato di New York dal 2021. Indice 1 Biografia 2 Note 3 Altri progetti 4 Collegamenti esterni Biografia Bowman è nato a Manhattan, New York City. Ha vissuto con...

محمود بورقيبة محمود بورقيبة معلومات شخصية الميلاد 26 سبتمبر 1910تونس العاصمة تونس تاريخ الوفاة 22 ماي 1956 الجنسية تونسية الحياة العملية الاسم الأدبي شاعر الشباب النوع شعر المهنة شاعر و صحفي اللغات العربية بوابة الأدب تعديل مصدري - تعديل محمود بورقيبة: هو محمود بن ال�...

Australian rules footballer and coach Australian rules footballer Bill Strickland Strickland during his Collingwood VFA careerPersonal informationDate of birth 17 August 1864Place of birth Sandhurst (Bendigo)Date of death 24 November 1959(1959-11-24) (aged 95)Place of death Sydney, New South WalesOriginal team(s) BrunswickPosition(s) CentrePlaying career1Years Club Games (Goals)1885–1888, 1890–1892 Carlton (VFA) 127 (4)1893–1896 Collingwood (VFA) 69 (1)1897 Collingwood 16 (0)Total ...
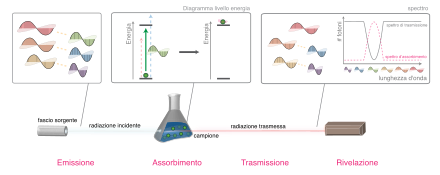
Disambiguazione – Se stai cercando tecniche spettroscopiche particolari, vedi Spettroscopia (disambigua). Schema di un'analisi mediante spettroscopio La spettroscopia, in chimica e fisica, indica la misurazione e lo studio di uno spettro elettromagnetico. Uno strumento che permette di misurare uno spettro viene chiamato spettrometro, spettrografo o spettrofotometro; quest'ultimo termine si riferisce ad uno strumento per la misura dello spettro elettromagnetico. La spettroscopia è la scien...
Computational method in Bayesian statistics Part of a series onBayesian statistics Posterior = Likelihood × Prior ÷ Evidence Background Bayesian inference Bayesian probability Bayes' theorem Bernstein–von Mises theorem Coherence Cox's theorem Cromwell's rule Likelihood principle Principle of indifference Principle of maximum entropy Model building Conjugate prior Linear regression Empirical Bayes Hierarchical model Posterior approximation Markov chain Monte Carlo Laplace's approximation I...

Powdrill v WatsonCourtHouse of LordsFull case name Powdrill v Watson, Talbot v Cadge Citation[1995] 2 AC 394, [1995] 2 WLR 312Court membershipJudges sittingLord Browne-Wilkinson, Lord Keith, Lord Mustill, Lord LloydKeywordsAdministration Powdrill v Watson [1995] 2 AC 394 is a UK insolvency law case concerning the administration procedure when a company is unable to repay its debts. Facts Roger Powdrill was a joint administrator of Paramount Airways Ltd, a short haul aircraft carrier. He wrot...