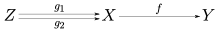Monomorfisme
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. And Millions Will DieNama alternatifAnd Millions Will Die!GenreCerita seruDitulis olehMichael FisherSutradaraLeslie H. MartinsonPemeranRichard BasehartSusan StrasbergLeslie NielsenJoseph FurstRowena WallaceMusikLaurie LewisNegara asalAustraliaAmerika Ser...

Julianne MooreMoore di Festival Film Internasional Venice ke-66, September 2009LahirJulie Anne Smith3 Desember 1960 (umur 63)Fort Bragg, North Carolina, Amerika SerikatKebangsaanBritania Raya-Amerika SerikatPekerjaanaktrisPenulis buku anak-anakTahun aktif1983 - sekarangSuami/istriJohn Gould Rubin (m. 1986–1995) Bart Freundlich (m. 2003) Julianne Moore (Julie Anne Smith; lahir 3 Desember 1960...

American judge For another person, see Charles J. Jenkins (Illinois politician). Charles Jones Jenkins44th Governor of GeorgiaIn officeDecember 14, 1865 – January 13, 1868Preceded byJames JohnsonSucceeded byThomas H. RugerAttorney General of GeorgiaIn office1831-1834 Personal detailsBorn(1805-01-06)January 6, 1805Beaufort, South CarolinaDiedJune 14, 1883(1883-06-14) (aged 78)Augusta, GeorgiaPolitical partyDemocraticAlma materUnion CollegeProfessionLawyer, politicianSignatu...

Amino acid that is incorporated biosynthetically into proteins during translation Proteinogenic amino acids are a small fraction of all amino acids Proteinogenic amino acids are amino acids that are incorporated biosynthetically into proteins during translation. The word proteinogenic means protein creating. Throughout known life, there are 22 genetically encoded (proteinogenic) amino acids, 20 in the standard genetic code and an additional 2 (selenocysteine and pyrrolysine) that can be incor...

American musician (born 1957) For other people named Michael Smith, see Michael Smith (disambiguation). Michael W. SmithSmith in March 2019BornMichael Whitaker Smith (1957-10-07) October 7, 1957 (age 66)Kenova, West Virginia, U.S.OccupationsMusicianactorworship leaderpastor (formerly)Spouse Deborah Kay Davis (m. 1981)Children5Musical careerOriginNashville, Tennessee, U.S.GenresCCMChristian rockpoppop rockInstrument(s)VocalskeyboardpianoguitarYears active198...

Pour les articles homonymes, voir Bravo. Cet article est une ébauche concernant une chaîne de télévision américaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. BravoCaractéristiquesCréation 8 décembre 1980Propriétaire NBCUniversal Television Group (en)Format d'image 480i, 1080iLangue AnglaisPays États-UnisStatut Généraliste nationale privéeSiège social GE BuildingSite web www.bravotv.comDiffus...

The Price of Salt Berkas:PriceOfSalt.JPGEdisi pertamaPengarang Patricia Highsmith Claire Morgan (nom de plume) NegaraAmerika SerikatBahasaInggrisGenreNovelDiterbitkan1952PenerbitCoward-McCann, W. W. Norton & Company (2004)Jenis mediaCetak (sampul keras & sampul kertas)Halaman276 hlm (ed. sampul keras)292 hlm (ed. sampul kertas, 2004)ISBNISBN 978-0-393-32599-7 (ed. 2004)OCLC1738553LCCPZ3.H53985 Pr(LCCN 52008026) The Price of Salt (kemudian diterbitkan ulang dengan judul Carol) ada...

Yoshimi MinamiLahir15 Desember 1915Prefektur Kagawa, JepangMeninggal25 November 1944(1944-11-25) (umur 28)FilipinaPengabdianKekaisaran JepangLama dinas1933-1944PangkatLetnanPerang/pertempuranPerang Dunia II:Perang Tiongkok-Jepang KeduaSerangan Pearl HarborPenyerbuan Samudera HindiaPertempuran Laut KarangPertempuran Laut FilipinaPertempuran Teluk LeytePertempuran Leyte Yoshimi Minami (南 義美code: ja is deprecated , Minami Yoshimi, 15 Desember 1915 – 25 November 19...

2013 single by Tamar BraxtonAll the Way HomeSingle by Tamar Braxtonfrom the album Love and War ReleasedAugust 21, 2013 (2013-08-21)Recorded2013GenreR&BsoulLength4:22LabelEpicSongwriter(s)Harvey Mason Jr.Damon ThomasMichael DaleySevyn StreeterSteven Lil Steve RussellJoelle JamesTerrence ColesProducer(s)The UnderdogsTamar Braxton singles chronology The One (2013) All the Way Home (2013) She Can Have You (2013) Music videoAll the Way Home on Youtube.com All the Way Home is a s...

American politician For other people named Richard Thompson, see Richard Thompson (disambiguation). Richard Thompson27th United States Secretary of the NavyIn officeMarch 13, 1877 – December 20, 1880PresidentRutherford B. HayesPreceded byGeorge M. RobesonSucceeded byNathan Goff Jr.Member of the U.S. House of Representativesfrom Indiana's 7th districtIn officeMarch 4, 1847 – March 3, 1849Preceded byEdward W. McGaugheySucceeded byEdward W. McGaugheyMember of th...

Idiom For the horse racing term, see Racecard. The Race Card redirects here. For other uses, see The Race Card (disambiguation). Cartoon by John Tenniel published following Abraham Lincoln's Emancipation Proclamation. The phrase itself came into use more than 100 years later. Playing the race card is an idiomatic phrase that refers to the exploitation by someone of either racist or anti-racist attitudes in the audience in order to gain an advantage.[1][2][3] It constit...

BuscaKomuneComune di BuscaNegaraItaliaWilayahPiedmontProvinsiProvinsi Cuneo (CN)FrazioniAttissano, Bosco, Castelletto, Morra San Giovanni, Sant'Alessio, San Barnaba, San Chiaffredo, San Martino, San Mauro, San Quintino, San Rocco, Santo Stefano, San VitaleLuas • Total65,8 km2 (254 sq mi)Ketinggian500 m (1,600 ft)Populasi (Dec. 2004) • Total9.671 • Kepadatan15/km2 (38/sq mi)DemonimBuschesiZona waktuUTC+1 (CET) • ...

Season of television series Agents of S.H.I.E.L.D.Season 7Promotional posterShowrunners Jed Whedon Maurissa Tancharoen Jeffrey Bell Starring Clark Gregg Ming-Na Wen Chloe Bennet Elizabeth Henstridge Henry Simmons Natalia Cordova-Buckley Jeff Ward No. of episodes13ReleaseOriginal networkABCOriginal releaseMay 27 (2020-05-27) –August 12, 2020 (2020-08-12)Season chronology← PreviousSeason 6List of episodes The seventh and final season of the American television series Ag...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

Viviane Reding Anggota Parlemen EropaMasa jabatan1 Juli 2014 – 1 September 2018Daerah pemilihanLuksemburgKomisaris Eropa untuk Keadilan, Hak Fundamental dan KewarganegaraanMasa jabatan9 Februari 2010 – 1 Juli 2014PresidenJosé Manuel BarrosoPendahuluJacques Barrot (Keadilan, Kebebasan dan Keamanan)PenggantiJohannes Hahn (Sementara)Komisaris Eropa untuk Masyarakat dan Media InformasiMasa jabatan22 November 2004 – 9 Februari 2010PresidenJosé Manuel BarrosoPenda...

حجر ويلاميت الذي اكتشف في ولاية أوريغون بالولايات المتحدة الرَّجْم[1] أو الحجر النيزكي[1] هو ما بقي من نيزك عند اصطدامه بسطح الأرض أو بسطح كوكب آخر. وتنتج حفرة عن أثر الاصطدام. ويعتقد العلماء أنها أجزاء من كويكبات أو مذنبات وعادة ما يتراوح أحجامها بين الصخور الصغيرة �...

PalauliDistrikLokasi di SamoaNegara SamoaIbu kotaVailoaLuas • Total523 km2 (202 sq mi)Populasi (2016) • Total9.317 • Kepadatan18/km2 (46/sq mi)Kode ISO 3166-2WS-PA Palauli adalah salah satu distrik di Samoa. Kode ISO 3166-2 distrik yang beribu kota di Vailoa ini adalah WS-PA. Menurut sensus 2016, jumlah penduduk distrik yang luasnya 523 kilometer persegi ini adalah 9.317 jiwa. Referensi Census 2016 Preliminary Count Report lbsD...

Direkt nach dem „Anschluss“ wurden die Wiener Juden unter Beteiligung der Bevölkerung gezwungen, in „Reibpartien“ pro-österreichische Slogans von den Gehsteigen zu putzen. Als Reibpartie bezeichnete man im österreichischen politischen Jargon der 1930er Jahre Gruppen von politischen Gegnern, die zum demütigenden öffentlichen Abwaschen, umgangssprachlich „Ausreiben“, das heißt Entfernen politischer Slogans, die den jeweiligen Machthabern unerwünscht waren, gezwungen wurden. I...

US federal government agricultural statistical agency National Agricultural Statistics ServiceAgency overviewFormed1863; 161 years ago (1863)JurisdictionFederal government of the United StatesHeadquartersWashington, D.C., U.S.Agency executiveHubert Hamer, AdministratorParent departmentUnited States Department of AgricultureWebsitehttp://www.nass.usda.gov/ Compiling the crop report in 1917 The National Agricultural Statistics Service (NASS) is the statistical branch of the U....

American pop band This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Before You Exit – news · newspapers · books · scholar · JSTOR (May 2024) (Learn how and w...