穆尔-彭罗斯广义逆
|
Read other articles:

Aldrin Petrus Mongan Komandan Lanud El TariMasa jabatan21 Januari 2022 – 9 November 2023 PendahuluUmar FathurrohmanPenggantiDjoko Hadipurwanto Informasi pribadiLahir24 Januari 1971 (umur 53)Laikit, Dimembe, Minahasa Utara, Sulawesi UtaraKebangsaanIndonesiaSuami/istriNy. Simon Petrus MonganAlma materAkademi Angkatan Udara (1992)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan UdaraMasa dinas1992—sekarangPangkat Marsekal Pertama TNISatuanKorps PenerbangSunting ...

For the Union Army officer, see Howard Mather Burnham. Mather Howard BurnhamM. Howard Burnham, 1915Born(1870-05-27)May 27, 1870Tivoli, Minnesota (near Mankato), United StatesDiedMay 4, 1917(1917-05-04) (aged 46)New York City, USBurial placeNew York City, New YorkNationalityAmericanAlma materMichigan Technological UniversityOccupation(s)Mining engineer, Spy[1]SpousesMargaretConstance Newton (Connie)Children4Parent(s)Rev Edwin Otway BurnhamRebecca Russell BurnhamEspionage acti...

Voci principali: Ducato di Milano, Governatore di Milano. Ducato di Milano (dettagli) (dettagli) Informazioni generaliCapoluogoMilano Popolazione750.000 (circa) Dipendente da Regno di Francia • Sacro Romano Impero Evoluzione storicaInizio6 settembre 1499 CausaTrattato di Trento (1501) Fine26 settembre 1525 CausaGuerra della Lega di Cambrai Preceduto da Succeduto da Ducato di Milano Ducato di Milano Cartografia Il Ducato di Milano cadde con intermittenza sotto dominazione francese nel primo...

Icelandic politician (born 1953) This is an Icelandic name. The last name is a family name, but this person is referred to by the given name Kristján. Kristján L. MöllerMinister of CommunicationsIn office24 May 2007 – 2 September 2010Prime MinisterGeir Haarde, Jóhanna SigurðardóttirPreceded bySturla Böðvarsson (as Minister of Communications and Transportation)Succeeded byÖgmundur Jónasson (as Minister of Transport, Communications and Local Government) Personal detailsBorn...

Hapoel Ramat Gan Giv'atayimCalcio Urduns Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Dati societari Città Ramat Gan, Giv'atayim Nazione Israele Confederazione UEFA Federazione IFA Campionato Liga Leumit Fondazione 1927 Allenatore Dani Golan Stadio Winter Stadium, Ramat Gan(8 000 posti) Sito web www.hapoelrg-fc.co.il Palmarès Titoli nazionali 1 Campionato di calcio israeliano Trofei nazionali 2 Coppe d'Israele Si invita a seguire il modello di voce Il Moadon K...
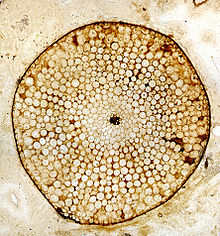
Extinct species of vascular plant RhyniaTemporal range: Early Devonian PreꞒ Ꞓ O S D C P T J K Pg N Reconstruction of Rhynia gwynne-vaughanii, redrawn after Kenrick & Crane (1997:101)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Subdivision: †Rhyniophytina Class: †Rhyniopsida Order: †Rhyniales Family: †Rhyniaceae Genus: †RhyniaKidst. & W.H.Lang (1917) Type species R. gwynne-vaughaniiKidst. & W.H.Lang (1917) Species R. gemuendensis Hirmer ...

Argentine association football player Nahuel Guzmán Guzmán with Tigres UANL in 2015Personal informationFull name Nahuel Ignacio Guzmán Palomeque[1]Date of birth (1986-02-10) 10 February 1986 (age 38)[2]Place of birth Rosario, Santa Fe, ArgentinaHeight 1.92 m (6 ft 4 in)[2]Position(s) GoalkeeperTeam informationCurrent team UANLNumber 1Youth career Newell's Old BoysSenior career*Years Team Apps (Gls)2005–2014 Newell's Old Boys 81 (0)2008–2009 �...

Construction of an angle equal to one third a given angle Angles may be trisected via a neusis construction using tools beyond an unmarked straightedge and a compass. The example shows trisection of any angle θ > 3π/4 by a ruler with length equal to the radius of the circle, giving trisected angle φ = θ/3. Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbi...

Norwegian radio and television personality Ada Haug and Odd Grythe in 1965 Odd Horn Grythe (14 November 1918 – 7 February 1995) was a Norwegian radio and television personality. Personal life He was born in Lillehammer as a son of a travelling salesman. He had four older siblings. From 1955 to 1958 he was married to Kirsten Sørlie. In March 1962 he married Ada Haug.[1] With his first wife he had the daughter Hilde Grythe, who married Terje Tønnesen.[2] Career He finished h...

Democratic politician from California John HoeppelMember of the U.S. House of Representativesfrom California's 12th districtIn officeMarch 4, 1933 – January 3, 1937Preceded byDistrict createdSucceeded byJerry Voorhis Personal detailsBornJohn Henry Hoeppel(1881-02-10)February 10, 1881Tell City, Indiana, U.S.DiedSeptember 21, 1976(1976-09-21) (aged 95)Arcadia, California, U.S.Political partyDemocraticOther politicalaffiliationsProhibition (1946) John Henry Hoeppel (F...

American basketball player For other people named Robert Gross, see Robert Gross (disambiguation). Bob GrossGross playing against the Boston Celtics on November 26, 1980Personal informationBorn (1953-08-03) August 3, 1953 (age 70)San Pedro, California, U.S.Listed height6 ft 6 in (1.98 m)Listed weight200 lb (91 kg)Career informationHigh schoolFermin Lasuen(San Pedro, California)College Seattle (1971–1972) Long Beach State (1973–1975) NBA draft1975: 2nd round, ...

Филиал Московского государственного университета имени М. В. Ломоносова в городе Ташкенте(филиал МГУ в Ташкенте) Международное название Tashkent Branch of Moscow State University Год основания 24 февраля 2006 года Руководитель филиала Часовских А.А. Студенты 434(397 — бакалавриат, 37 — магистрат...

Chronologies Données clés 1996 1997 1998 1999 2000 2001 2002Décennies :1960 1970 1980 1990 2000 2010 2020Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

Not to be confused with I'm Your Pusher (Scooter song). 1988 single by Ice-TI'm Your PusherSingle by Ice-Tfrom the album Power B-sideGirls L.G.B.N.A.F.ReleasedAugust 23, 1988StudioSyndicate Studios West (Los Angeles, California)GenreGangsta rapLength5:35LabelSireSongwriter(s) Tracy Marrow Charles Glenn Curtis Mayfield Producer(s) Ice-T Afrika Islam Ice-T singles chronology Colors (1988) I'm Your Pusher (1988) High Rollers (1988) Music videoI'm Your Pusher on YouTube I'm Your Pusher is a 1988 ...

عبد الحليم اللاوند معلومات شخصية الميلاد 29 أغسطس 1934 الموصل الوفاة سنة 2000 بغداد مواطنة المملكة العراقية الجمهورية العراقية الجمهورية العراقية الحياة العملية المهنة شاعر، وكاتب تعديل مصدري - تعديل عبد الحليم عبد المجيد اللّاوند (29 آب/أغسطس 1934 - 20...

Orang kulit hitam yang terkenalAtas: W.E.B. Du Bois, MLK dan Nelson MandelaBawah: Wangari Maathai, Rosa Parks, Sojourner Truth Seorang wanita Kongo Orang kulit hitam adalah sebuah istilah yang digunakan di negara-negara tertentu, sering kali secara sosial berdasarkan pada sistem klasifikasi rasial atau etnisitas, untuk menyebut orang yang berkulit hitam dibandingkan dengan penduduk lainnya. Karena itu, pengatiannya banyak ragamnya di dalam maupun antar masyarakat, dan tergantung pada konteks....

Portuguese association football club For other uses, see Benfica (disambiguation). Football clubBenfica e Castelo BrancoFull nameSport Benfica e Castelo BrancoNickname(s)Águia Albicastrense (Castelo Branco Eagles)[1]AlbicastrensesFounded24 March 1924; 100 years ago (24 March 1924)GroundEstádio Municipal Vale do Romeiro, Castelo BrancoCapacity12,000ChairmanJorge NevesManagerDani MatosLeagueCampeonato de Portugal2022-23Serie C, 5thWebsiteClub website Sport Benfica e Caste...

لمعانٍ أخرى، طالع هارتفورد (توضيح). هارتفورد الإحداثيات 44°22′22″N 70°20′48″W / 44.372777777778°N 70.346666666667°W / 44.372777777778; -70.346666666667 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة أكسفورد خصائص جغرافية المساحة 45.08 ميل مربع ...

Extinct Celtic languages of Iberia Hispano-CelticGeographicdistributionIberian PeninsulaLinguistic classificationIndo-EuropeanCelticContinental CelticHispano-CelticSubdivisions Celtiberian † Gallaecian † Language codes Part of a series onIndo-European topics Languages List of Indo-European languages Extant Albanoid Albanian Armenian Balto-Slavic Baltic Slavic Celtic Germanic Hellenic Greek Indo-Iranian Indo-Aryan Iranian Nuristani Italic Romance Extinct Anatolian Tocharian Paleo-Balkan Da...

French physician and psychologist (1859–1947) For the 19th-century French bibliographer, see Pierre Jannet (bibliographer). You can help expand this article with text translated from the corresponding article in French. (June 2012) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary an...





















































































































