Phép Äo lÆḞáṠ£ng táṠ yáẃṡu
|
Read other articles:

James WatsonJames WatsonLahirJames Dewey Watson06 April 1928 (umur 95)[1]Chicago, Illinois, Amerika SerikatKebangsaanAmerika SerikatAlmamater Universitas Chicago (B.S., 1947) Universitas Indiana (Ph.D., 1950) Dikenal atas Struktur DNA Biologi molekular Suami/istriElizabeth Watson (née Lewis) (m. 1968)Penghargaan Penghargaan Albert Lasker untuk Penelitian Kedokteran Dasar (1960) Hadiah Nobel (1962) Penghargaan John J. Carty (1971) ForMemRS ...

Artikel ini bukan mengenai Bangsa Sarmatia. Orang Samaria Israelite Samaritan atau Orang Samaria adalah penduduk wilayah Israel bagian utara, yang dulunya menjadi wilayah Kerajaan Israel.[1] Sejak abad ke-6 SM, ada pertentangan antara orang-orang Samaria dengan orang-orang Yahudi, yang berlangsung hingga masa Perjanjian Baru.[1] Pertentangan tersebut terutama disebabkan alasan etnisitas, yang mana orang-orang Yahudi menganggap orang-orang Samaria tidak berdarah Israel murni ka...

Stress from contradictory beliefs Part of a series onPsychology Outline History Subfields Basic psychology Abnormal Affective neuroscience Affective science Behavioral genetics Behavioral neuroscience Behaviorism Cognitive/Cognitivism Cognitive neuroscience Social Comparative Cross-cultural Cultural Developmental Differential Ecological Evolutionary Experimental Gestalt Intelligence Mathematical Moral Neuropsychology Perception Personality Positive Psycholinguistics Psychophysiology Quantitat...

Japanese manga series Air MasterFirst tankÅbon volume coverãẀãḃããṗãṡãỳ(Ea MasutÄ)GenreComedy[1]Martial arts[2] MangaWritten byYokusaru ShibataPublished byHakusenshaImprintJets ComicsMagazineYoung AnimalDemographicSeinenOriginal run1996 â 2006Volumes28 Anime television seriesDirected byDaisuke NishioProduced byHiroshi YamashitaManabu TamuraAtsushi KidoWritten byMichiko YokoteMusic byYoshihisa HiranoStudioToei AnimationLicensed byCru...

Abjad writing system Libyco-Berber alphabetScript type Abjad Time periodSometime during the first millennium BC to the 4th-7th century ADDirectionVarious, but usually bottom-to-top or right-to-leftLanguagesNumidian language, Libyco-Berber (ancient or classical Berber language)Related scriptsParent systemsEgyptian hieroglyphsProto-Sinaitic script? Early Berber Script[1]Libyco-Berber alphabetChild systemsTifinagh (Tuareg Tifinagh) The Libyco-Berber alphabet or the Libyc alphabet is an a...

ŴċÑŴẁÑÑŴẁŴḞŴẄÑÑŴĠŴẅŴŴẁŴḟŴṠŴẁÑ ŴŴṁÑÑ ŴẁŴṗ ŴŴḞŴĠŴṁÑ ŴŴẅŴĠÑŴṗ ŴŴḞŴĠŴṁÑ ŴŴĠŴḞŴẄŴġŴṁŴṠŴẁŴṁ ŴŴṁÑÑÑÑ ŴṖŴḞŴṡŴẅŴĠŴṁŴṀŴṁŴṗ ŴŴḞŴġŴẅÑŴẄŴḞÑ ŴṡÑŴẅŴṡŴẅŴĠŴṁŴṀÑ ŴŴṡŴẅŴẃÑŴẁÑÑ ŴŴẅŴġ, ŴḃÑŴẅŴẁÑŴḞ ŴŴẅŴġ ŴÑŴṁÑ ŴŴẁÑÑÑ ŴċÑŴẁÑÑŴẅÑ ŴḂŴĠÑÑŴẅŴṗ ŴÑÑ ŴÑÑŴẅÑŴẁÑ Ñ ÑŴẁÑÑŴẁŴḞŴẄÑÑŴĠŴḞ ŴŴṡŴẅÑÑŴẅŴṠÑ ŴċÑŴẅŴẄŴẅŴṠŴẅŴġŴẁÑ Ñ ÑŴẁÑÑŴẁŴḞŴẄÑÑŴĠŴḞ Ŵ ŴḞŴẄŴẄŴṁŴṁ Ñ ÑŴẁÑÑŴẁŴḞŴẄÑÑŴĠŴẅ ŴŴẄŴẅÑÑŴẁÑŴṁÑŴẃŴẅŴṁ Ñ ÑŴẁÑÑŴẁŴḞŴẄÑÑŴĠŴẅ ŴÑŴṁŴṠŴṁŴẄÑŴẃŴẁŴṁ ÑŴẅŴḟŴẅÑÑ Ŵ...
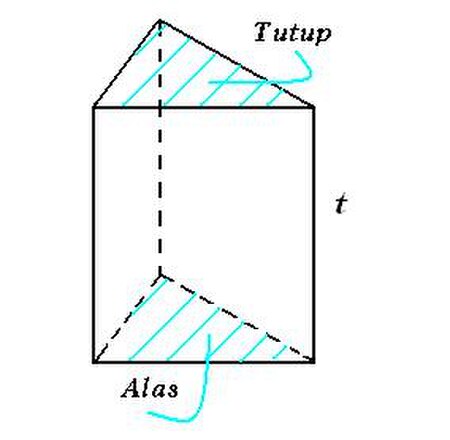
Untuk kegunaan lain, lihat Prisma (disambiguasi). Sebuah prisma segitiga dengan tinggi t Dalam geometri, prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Dengan kata lain prisma adalah bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran. Prisma segi-n memiliki n + 2 sisi, 3n rusuk dan 2n titik sudut. Prisma dengan alas dan tutup berbentuk persegi d...

ŴŴṁÑŴ¶ŴḞŴĠŴẄŴẁŴṗ ŴẃŴẅŴỳÑÑŴṁÑ ÑŴṁŴṠŴṁŴḟŴḞÑŴṁŴẄŴẄÑ Ñ ÑŴḞŴṀÑŴẅŴỳŴẅŴĠŴṠŴṁŴẄŴẄÑ Ŵ£ŴẃÑŴḞÑŴẄŴẁ (ŴŴṁÑŴ¶ŴẃŴẅŴỳÑŴṁŴṠŴṁÑŴḞŴṀÑŴẅ) ŴÑŴẁŴỳÑÑŴṁŴẄŴẄÑ ŴẃŴẅŴỳÑÑŴṁÑÑŴŴḞŴġŴḞŴṠÑŴẄŴḞ ÑŴẄÑŴẅÑŴỳŴḞÑÑÑŴÑŴḞÑŴẄŴḞ Ŵ£ŴẃÑŴḞÑŴẄŴḞŴŴḞÑŴḞ ÑÑŴĠŴẅÑŴṁŴẄŴẄÑ 2003ŴŴṁÑÑŴĠŴẄŴṁ ŴĠÑŴṀŴẅŴỳÑÑŴĠŴẅ ŴŴḞŴḟÑŴẄŴṁÑ ŴÑŴẄÑÑÑÑÑŴĠ Ŵ£ŴẃÑŴḞÑŴẄŴẁŴ ÑÑŴẄŴẁŴṗ ŴḟÑŴṀŴ¶ŴṁÑ 1 964 898 500 âṀ[1]ŴŴẅŴṠŴẅŴĠŴḞ ŴŴṠŴṁŴġ ŴŴḞŴṠŴẁŴĠŴḞŴṗŴẃŴẅŴÑŴṀŴĠÑŴṀŴẅŴỳÑÑ ŴẅÑ...

Christophe Jallet Informasi pribadiNama lengkap Christophe JalletTanggal lahir 31 Oktober 1983 (umur 40)Tempat lahir Cognac, PrancisTinggi 1,78 m (5 ft 10 in)Posisi bermain BekInformasi klubKlub saat ini Paris Saint-GermainNomor 26Karier junior1992-1998 Cognac1998â2003 NiortKarier senior*Tahun Tim Tampil (Gol)2003â2006 Niort 98 (12)2006â2009 Lorient 97 (3)2009â Paris Saint-Germain 102 (7)Tim nasionalâḂ2012â Prancis 3 (1) * Penampilan dan gol di klub senior hany...

Former British music label Castle Communications PLCCompany typePrivateIndustryPublishing, distributionGenreMusical reissues and repertoireFounded1983 (1983)FounderTerry Shand, Cliff Dane, Jon BeecherDefunct2007 (2007)FateDissolvedHeadquartersChessington, Greater London, United KingdomArea servedWorldwideParentAlliance Entertainment (from 1994)Sanctuary Records Group (from 2000)DivisionsDojo Ltd.Raw Power Castle Communications, also known as Castle Music,[1] was a British in...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Sitora FarmonovaInformasi latar belakangNama lahirSitora FarmonovaLahir20 Agustus 1984 (umur 39)AsalBukhara, Republik Sosialis Soviet Uzbekistan, Uni SovietGenrePopPekerjaanPemeran, penyanyiTahun aktif2000âsekarang Sitora Farmonova (bahasa Uzbe...

Province in Papua New Guinea Place in Papua New GuineaMorobe Province Morobe Provins (Tok Pisin) FlagMorobe Province in Papua New GuineaCoordinates: 6ÂḞ50âĠS 146ÂḞ40âĠE / 6.833ÂḞS 146.667ÂḞE / -6.833; 146.667CountryPapua New GuineaCapitalLaeDistricts List Bulolo DistrictFinschhafen DistrictHuon DistrictKabwum DistrictLae DistrictMarkham DistrictMenyamya DistrictNawae DistrictTewae-Siassi District Government âḃ GovernorLuther Wenge 2022â2027Area ...

ÙÙ ØṗاÙ٠أخØḟÙØ ØṖاÙØṗ Ù ØĊØṀØḟ (ØẂÙضÙØ). Ù ØĊØṀØḟ اÙØẂÙÙ ÙØ© اÙØẀØṀØḟÙØ©Ù ØṗÙÙ٠اØẂ Øṗا٠ةØṁÙÙ ÙØḟØṗÙ Ù Ù ÙÙ ÙØ© Ùا ØẀØṗØŸÙØ© ØỲاÙØẀ Ù Ù ØỲÙاÙØẀ ØẂØṖÙØḟ اÙØċÙØġا٠اÙاØġ٠اÙÙ Ø®ØẂØṁØḟ HDI (ØẀاÙØċÙØỲÙÙØĠÙØ©) IDH (ØẀاÙÙØḟÙØġÙØ©) IDH (ØẀاÙØċØġØẀاÙÙØ©) اÙÙ ÙØẂØṀ٠أ٠اÙÙ Ø®ØẂØḟØṗ Ù ØØẀÙØẀ اÙØÙأ٠اØḟØẂÙا ØġÙMeghnad Desai, Baron Desai (en) اÙØẀØṗØŸ ØØġØẀ اÙÙØẁا٠اÙØŸÙÙÙ ÙÙÙÙ ÙاØẂ 1 ...

Debt incurred by individuals due to health care costs The examples and perspective in this article deal primarily with the United States and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (January 2019) (Learn how and when to remove this message) Medical debt refers to debt incurred by individuals due to health care costs and related expenses, such as an ambulance ride or the cost of ...

Bilateral relationsRelations between France and the Democratic Republic of Congo France DR Congo DR CongoâFrance are the bilateral diplomatic relations between the Democratic Republic of the Congo and France. Both nations are members of the Organisation internationale de la francophonie and the United Nations. History This section needs expansion. You can help by adding to it. (March 2023) In 1961, France sent colonel Roger Trinquier to support the coup d'etat of Mobutu Sese Seko.[1]...
Peta Teluk Dublik di Pulau Irlandia Teluk Dublin (bahasa Irlandia: Cuan Bhaile Ãtha Cliath, bahasa Inggris: Dublin Bay) adalah inlet berbentuk C dari Laut Irlandia di pantai timur Republik Irlandia. Teluk ini lebarnya sekitar 10 kilometer di sepanjang pangkalan utara-selatan, dan panjangnya 7 km ke puncaknya di pusat kota Dublin; membentang dari Howth Head di utara ke Dalkey Point di selatan. North Bull Island terletak di bagian barat laut teluk, di mana salah satu dari dua tepian pa...

United States law Conservation status by IUCN Red List categoryExtinctExtinct (EX)Extinct in the Wild (EW)(list)(list)ThreatenedCritically Endangered (CR)Endangered (EN)Vulnerable (VU)(list)(list)(list)Lower RiskNear Threatened (NT)Conservation Dependent (CD)Least Concern (LC)(list)(list)Other categoriesData Deficient (DD)Not Evaluated (NE)(list)Related topics International Union forConservation of Nature (IUCN) IUCN Red List NatureServe status Lists of organisms by population Comparison of R...

ØỲاØḊØĠØ© ØẀÙØỲÙÙا اÙÙØẀØḟÙ 1977 اÙØġØẀا٠7 ٠٠أØṁÙ 17 ÙÙ ØẀØṖÙÙØ© اÙØṗاÙÙ ÙØġØẀاÙاØẂ اÙÙÙØḟÙ ÙÙا ÙاØØŸ Ù ÙØġÙ 1977 اÙØġÙØġÙØ© ØẀØṖÙÙØ© اÙØṗاÙÙ ÙØġØẀاÙاØẂ ÙÙØḟÙ ÙÙا 1 Ù ÙØġÙ 1977 اÙØẀÙØŸ ØẀÙØỲÙÙا اÙØẂاØḟÙØ® 5 ÙÙÙÙÙ 1977 Ù Ùا٠اÙØẂÙØẁÙÙ ØÙØẀØ© ØĠÙÙØŸØḟ [ÙØẃاØẂ أخØḟÙ] ØṖÙ٠اÙÙ ØġاØḟ 4.011 ÙÙÙÙÙ ØẂØḟ (2.492 Ù ÙÙ) اÙÙ ØġاÙØ© 280.77 ÙÙÙÙÙ ØẂïṡẄ...

èẀäỳæỲ§åẁçḊSailly-au-Bois æġååẁé åẅẄçḋ èẀäỳæỲ§åẁçḊçäẄçẄ® èẀäỳæỲ§åẁçḊæẅçĊẃæġåẄçåḞåẅèẀäỳæỲ§åẁçḊæẅçĊẃå æċæṁṖåġḂççåḞåẅåæ ïỳ50ÂḞ07âĠ14âġN 2ÂḞ35âĠ43âġE / 50.1206ÂḞN 2.5953ÂḞE / 50.1206; 2.5953åẄ家 æġååĊ§åẃ äẁæġèèċṡåĊ§åç å æċæṁṖåġḂçåẃéṡææŸåẃéḃ租1 âḃ åẁé9.28 åṗġæṗå Ỳéïỳ3.58 åṗġæṗèḟéïỳäẃẃå£ïỳ2021åṗṀïỳ[1] âḃ åẁé294äẃẃ âḃ&...

Cet article est une ébauche concernant la politique québécoise. Vous pouvez partager vos connaissances en lâaméliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Louis Hébert (homonymie) et Hébert. Louis-Hébert Circonscription électorale provinciale du CanadaDonnées clés Création 1965 Localisation Province Québec Superficie 36,93 km2 Représentation politique Députée GeneviÃẀve Guilbault Parti politique Coalit...





































