NhÃģm thÆ°ÆĄng
|
Read other articles:

Leandro Trossard Trossard bersama Brighton & Hove Albion pada 2022Informasi pribadiNama lengkap Leandro Trossard[1]Tanggal lahir 4 Desember 1994 (umur 29)Tempat lahir Maasmechelen, BelgiaTinggi 172 cm (5 ft 8 in)[2]Posisi bermain SayapInformasi klubKlub saat ini ArsenalNomor 19Karier senior*Tahun Tim Tampil (Gol)2012â2019 Genk 83 (27)2012â2013 â Lommel United (pinjaman) 12 (7)2013â2014 â Westerlo (pinjaman) 17 (3)2014â2015 â Lommel United...

اŲØđŲاŲا؊ اŲØđŲ اŲŲØĐ Ø§ŲŲŲØąŲØĐ Ø§ŲØīŲ اŲŲØĐ ØģŲØ·ŲØĐ ØđŲ اŲ ŲŲØąŲا اŲØīŲ اŲŲØĐ ØģŲØ·ŲØĐ ØđŲ اŲ ŲŲØąŲا اŲØīŲ اŲŲØĐ ØŠØđØŊŲŲ Ų ØĩØŊØąŲ - ØŠØđØŊŲŲ اŲØđŲاŲا؊ اŲØđŲ اŲŲØĐ Ø§ŲŲŲØąŲØĐ Ø§ŲØīŲ اŲŲØĐ ŲŲ اŲØđŲاŲا؊ اŲØŦŲاØĶŲØĐ Ø§ŲØŠŲ ØŠØŽŲ Øđ ØĻŲŲ ØģŲØ·ŲØĐ ØđŲ اŲ ŲŲŲØąŲا اŲØīŲ اŲŲØĐ.[1][2][3][4][5] Ų ŲØ§ØąŲØĐ ØĻŲŲ اŲØĻŲØŊŲ...

Indirect conflict between Iran and Saudi Arabia IranâSaudi Arabia proxy conflictPart of the Arab WinterMap of the current situation in the conflict: Iran Saudi Arabia Proxy conflict locationsDate11 February 1979 â ongoing[74][75](45 years, 1 month, 3 weeks and 2 days)LocationVarious (primarily Middle East)Belligerents Iran Proxies:[1] Hezbollah Al-Hejaz[2] OIRAP[3](1979â1988)[4] Liwa Fa...

Election in New Mexico Main article: 1928 United States presidential election 1928 United States presidential election in New Mexico ← 1924 November 6, 1928 1932 → Nominee Herbert Hoover Al Smith Party Republican Democratic Home state California New York Running mate Charles Curtis Joseph T. Robinson Electoral vote 3 0 Popular vote 69,645 48,211 Percentage 59.01% 40.85% County Results Hoover 50-60% 60-70% 70-...

Druid gathering at Stonehenge Ukrainian temple of the RUNVira in Spring Glen, New York Modern paganism, also known as contemporary or neopagan, encompasses a wide range of religious groups and individuals. These may include old occult groups, those that follow a New Age approach, those that try to reconstruct old ethnic religions, and followers of the pagan religion or Wicca. Early movements Pre-World War II neopagan or proto-neopagan groups, growing out of occultism and/or Romanticism (Medi...

This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (August 2014) (Learn how and when to remove this template message) House of De Silva FernÃĄndez de HÃjar Portugal No pose quien mal posa.[1][2]CountrySpain, Portugal, ItalyFoundedFirst hypothesis: 900 d.c.; second hypothesis: 1030 d.c.FounderFirst hypothesis: Aznar Fruela, Infante de Leon ; Second hypothesis: Gutierres PelÃĄ...
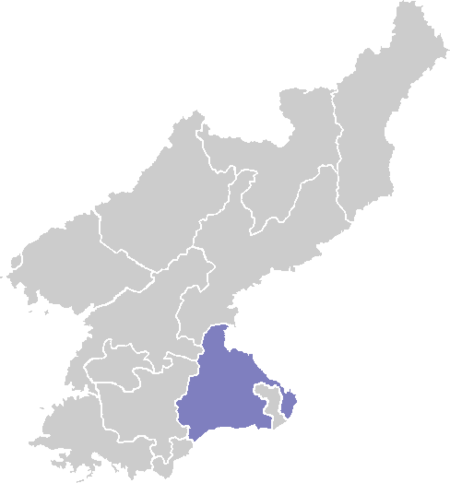
For the community in the U.S., see Sepo, Illinois. Not to be confused with Seppo. County in KangwÅn Province, North KoreaSep'o County ėļíŽęĩ°CountyėļíŽęĩ° · Sepo CountyKorean transcription(s) âĒ ChosÅn'gÅlėļíŽęĩ° âĒ HanchaæīæĩĶéĄ âĒ McCuneâReischauerSep'o-gun âĒ Revised RomanizationSepo-gunMap of Kangwon showing the location of SepoCountryNorth KoreaProvinceKangwÅn ProvinceAdministrative divisions1 Åp, 1 workers' d...

German-American actor In this article, the surname is van Eyck, not Eyck. Peter van EyckTrailer for Five Graves to Cairo (1943)BornGÃķtz von Eick(1911-07-16)16 July 1911Steinwehr, Pomerania, German Empire(present-day Kamienny Jaz, West Pomeranian Voivodeship, Poland)Died15 July 1969(1969-07-15) (aged 57)MÃĪnnedorf, near ZÞrich, SwitzerlandCitizenshipWest GermanyUnited States (after 1943)OccupationActorYears active1943–1969Spouse(s)Ruth Ford(m. 1940; div. 194?)Inge von Voris(m...

Concentration of population defined by the United States Census Bureau This article is part of a series onPolitical divisions ofthe United States First level State (Commonwealth) Federal district Territory (Commonwealth) Indian reservation (list) / Hawaiian home land / Alaska Native tribal entity / Pueblo / Off-reservation trust land / Tribal Jurisdictional Area Second level County / Parish / Borough Unorganized Borough / Census area / Villages / District (USVI) / District (AS) Consolidated c...

Matteo Perego di Cremnago Sottosegretario di Stato al Ministero della difesaIn caricaInizio mandato2 novembre 2022 ContitolareIsabella Rauti Capo del governoGiorgia Meloni PredecessoreGiorgio MulÃĻStefania Pucciarelli Deputato della Repubblica ItalianaDurata mandato23 marzo 2018 –12 ottobre 2022 LegislaturaXVIII GruppoparlamentareForza Italia-Berlusconi Presidente CoalizioneCentro-destra 2018 CircoscrizioneLombardia 4 Incarichi parlamentari Vice-capogruppo di Forza I...

Kalender Kelt adalah kumpulan dari sistem penanggalan waktu suku bangsa Kelt pra-Kekristenan (termasuk kalender Coligny). Kalender ini terdiri dari pembagian hari, minggu, bulan, musim, seperempat hari, dan perayaan.[1] Kalender Kelt Benua Informasi lebih lanjut: Kalender Coligny Ikhtisar pecahan kalender yang dipasang kembali yang ditemukan di Coligny, Prancis. Kalender Coligny yang dibuat oleh suku Galia adalah kalender keagamaan suryacandra Kelt tertua yang diketahui. Kalender ini ...

Integers have unique prime factorizations Not to be confused with Fundamental theorem of algebra. In Disquisitiones Arithmeticae (1801) Gauss proved the unique factorization theorem [1] and used it to prove the law of quadratic reciprocity.[2] In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up t...
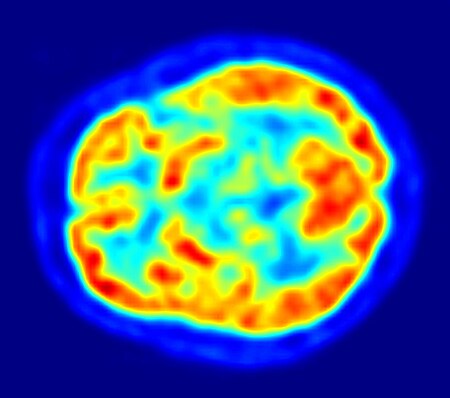
Diagnostic imaging test in nuclear medicine ScintigraphyScintigraphyICD-9-CM92.0-92.1MeSHD011877OPS-301 code3-70[edit on Wikidata] Scintigraphy (from Latin scintilla, spark), also known as a gamma scan, is a diagnostic test in nuclear medicine, where radioisotopes attached to drugs that travel to a specific organ or tissue (radiopharmaceuticals) are taken internally and the emitted gamma radiation is captured by gamma cameras, which are external detectors that form two-dimensional im...
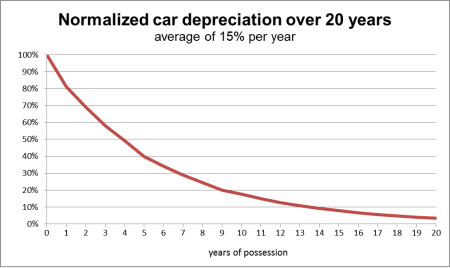
Not to be confused with Deprecation. This article is about the concept in accounting and finance involving fixed capital goods. For economic depreciation, see Depreciation (economics) and Fixed capital § Economic depreciation. For the decrease in value of a currency, see Currency depreciation. Decrease in asset values, or the allocation of cost thereof An asset depreciation at 15% per year over 20 years In accountancy, depreciation is a term that refers to two aspects of the same concep...

ŲØ°Ų اŲŲ ŲاŲØĐ ŲØŠŲŲ ØĐ ØĨØ° ØŠØĩŲ ØĨŲŲŲا Ų ŲاŲا؊ ØĢØŪØąŲ ŲŲŲŲØĐ ØŽØŊŲا. ŲØķŲŲØ§Ø ØģاØđØŊ ØĻØĨØķاŲØĐ ŲØĩŲØĐ ØĨŲŲŲا ŲŲ Ų ŲاŲا؊ Ų ØŠØđŲŲØĐ ØĻŲا. (ØŊŲØģŲ ØĻØą 2020) Ų اŲŲŲŲ ŲŲŲ ØĻŲØąØŠŲ ŲŲ؊ا ØŪŲŲ ŲŲŲØē (ØĻاŲØĨØģØĻاŲŲØĐ: Manuel Humberto Cota JimÃĐnez)â Ų ØđŲŲŲ ا؊ ØīØŪØĩŲØĐ Ø§ŲŲ ŲŲاØŊ 2 Ų Ø§ØąØģ 1961 (63 ØģŲØĐ) ØŠØĻŲŲ Ų ŲاطŲØĐ Ø§ŲŲ ŲØģŲŲ Ų ŲاØĩØĻ اŲØŲاØĐ Ø§ŲØđŲ ŲŲØĐ Ø§Ų...

American baseball player (born 1970) Not to be confused with Jim Edmond. Baseball player Jim EdmondsEdmonds with the San Diego Padres in 2008Center fielderBorn: (1970-06-27) June 27, 1970 (age 54)Fullerton, California, U.S.Batted: LeftThrew: LeftMLB debutSeptember 9, 1993, for the California AngelsLast MLB appearanceSeptember 21, 2010, for the Cincinnati RedsMLB statisticsBatting average.284Home runs393Runs batted in1,199 Teams California / Anaheim Angels (1...

Neue Freie Presse ist eine Weiterleitung auf diesen Artikel. Zur Jugendzeitschrift siehe GÞnther Nenning#Journalismus. Die Presse war ein Titel der Thorner Presse. Die Presse Beschreibung Ãķsterreichische Tageszeitung Verlag Die Presse Verlags-Gesellschaft m.b.H. & Co KG Erstausgabe 3. Juli 1848 Erscheinungsweise tÃĪglich, am Sonntag jedoch als âDie Presse am Sonntagâ Verkaufte Auflage 66.670 (MontagâSamstag);68.761(Sonntag) Exemplare (ÃAK 1. Halbjahr 2021[1]) Reichw...

Cargo airline based in Louisville, Kentucky, United States UPS Airlines IATA ICAO Callsign 5X UPS UPS Founded1988 (successor to UPS air cargo that began in 1929)AOC #IPXA097B[1]Hubs Worldport Louisville Asia/Pacific Clark[2] Hong Kong[3] Kuala LumpurâInternational[4] ShanghaiâPudong[5] Shenzhen[6] Canada Hamilton (ON) Caribbean Carolina (Puerto Rico) Europe Cologne/Bonn East Midlands (England) United States Anchorage Columbia (SC) Chica...

Further information: List of plants of the Sierra Nevada (U.S.) § Alpine Zone, and Ecology of the Sierra Nevada § Alpine Zone The brightly colored sky pilot (Polemonium eximium), considered to be among the most beautiful of the Sierra Nevada wildflowers, grows in very harsh conditions to elevations of 13,000 feet (4,000 m), which is near the upper limit of plant growth in California. The flora of the U.S. Sierra Nevada alpine zone is characterized by small, low growing, cush...

Original DeskJet 500 DeskJet 3845 Deskjet is a brand name for inkjet printers manufactured by Hewlett-Packard.[1] These printers range from small domestic to large industrial models, although the largest models in the range have generally been dubbed DesignJet.[2] The Macintosh-compatible equivalent was branded as the Deskwriter and competed with Apple's StyleWriter, and the all-in-one equivalent is called OfficeJet. HP's first inkjet printer is the ThinkJet. A modern HP Deskj...







































































