Chu kỳ quỹ đạo
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Parlemen Sierra LeoneJenisJenisUnikameral PimpinanSpeakerAbass Bundu, sejak 25 April 2018, SLPP KomposisiAnggota146 (132 dipilih + 14 ditunjuk)Partai & kursi Kongres Semua Rakyat (68) Partai Rakyat Sierra Leone (49) Koalisi untuk Perubahan (8) Koalisi Besar Nasional (4) Independen (3) Kepala tertinggi (14) PemilihanSistem pemilihanFirst-past-the-postPemilihan terakhirJuni 2023Tempat bersidang Gedung Parlemen, Tower Hill, FreetownSitus webwww.p...

Dalam nama Korean ini, nama keluarganya adalah Baek. Baek Il-seobLahir10 Juni 1944 (umur 79)Yeosu, Provinsi Jeolla Selatan, Korea SelatanPendidikanUniversitas Myongji Sastra InggrisPekerjaanAktorTahun aktif1965-sekarangNama KoreaHangul백일섭 Hanja白一燮 Alih AksaraBaek Il-seopMcCune–ReischauerPaek Il-sŏp Baek Il-seob (Hangul: 백일섭; lahir 10 Juni 1944) adalah aktor film dan televisi asal Korea Selatan.[1] Ia tampil dalam drama Mom's Dead Upset,[2 ...

1971 film by Herbert B. Leonard Going HomeTheatrical release posterDirected byHerbert B. LeonardScreenplay byLawrence B. MarcusProduced byHerbert B. LeonardStarringRobert MitchumBrenda VaccaroCinematographyFred Jackman Jr.Edited bySigmund Neufeld Jr.Music byBill WalkerProductioncompanyMetro-Goldwyn-MayerRelease date1 December 1971Running time97 minutesCountryUnited StatesLanguageEnglish Going Home is a 1971 drama film directed by Herbert B. Leonard and starring Robert Mitchum, Brenda Vaccaro ...

Сидят (слева направо): Федр Гаглоев (Гафез), Резо Чочиев, Лади Газзаев, Пауле Санакоев, Елиоз Бекоев, Георгий Джаттиев. Стоят (слева направо): Алекси Букулов, Нафи Джусойты, Реваз Асаев, Петр Пухаев, Георгий Дзугаев, Ила Плиев, Григол Гаглоев Осети́нская литерату́ра (осет. Иро�...

Mountain CourseLokasiDouglas, Isle of ManZona waktuBritish Summer Time (selama musim acara)Acara besarIsle of Man TT, Manx Grand Prix Grand Prix sepeda motor MotoGPPanjang60.725 km (37.73 mi)Tikungan219Rekor lap16 menit 42.778 detik - rata-rata 135.452 mph (Peter Hickman, BMW, 2018) Isle of Man TT Mountain Course atau TT Course[1] adalah sirkuit sepeda motor balap jalanan yang terletak di Pulau Man. Sepeda motor TT Course digunakan terutama untuk Balapan Isle of Man TT dan juga acara ...

Voce principale: Association Sportive Saint-Raphaël Volley-Ball. Association Sportive Saint-Raphaël Volley-BallStagione 2015-2016Sport pallavolo Squadra Saint-Raphaël Allenatore Giulio Bregoli All. in seconda Christophe Guibert Presidente Christine Girod Ligue A7ª Play-off scudettoVincitrice Coppa di FranciaQuarti di finale Miglior marcatoreCampionato: Vindevoghel (456) 2014-15 2016-17 Questa voce raccoglie le informazioni riguardanti l'Association Sportive Saint-Raphaël Volley-Bal...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Annual integral calculus competition Finalists of the 2006 MIT Integration Bee, with the champion, dubbed the Grand Integrator, in the middle.Part of a series of articles aboutCalculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem Differential Definitions Derivative (generalizations) Differential infinitesimal of a function tota...
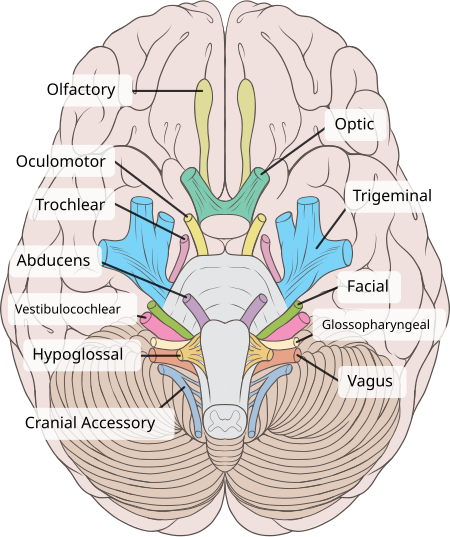
Trochlear nervePath of the Trochlear nerveInferior view of the human brain, with the cranial nerves labelled.RincianPersarafansuperior oblique musclePengidentifikasiBahasa Latinnervus trochlearisMeSHD014321NeuroNames466TA98A14.2.01.011TA26191FMA50865Daftar istilah neuroanatomi[sunting di Wikidata] Saraf Kranial CN I – Olfaktorius CN II – Optikus CN III – Okulomotor CN IV – Troklearis CN V – Trigeminus CN VI – Abdusen CN VII – Fasialis CN VIII – Vestibulokoklearis CN IX –...

Запрос «Скот» перенаправляется сюда; см. также другие значения. Ягнёнок Сельскохозя́йственные живо́тные — содержащиеся человеком для получения продуктов питания (мясо, молоко, яйца), жира, сырья производства (шерсть, мех, пух), щетины, кожи, костей, перьев, а также выпол�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

العلاقات السنغالية الوسط أفريقية السنغال جمهورية أفريقيا الوسطى السنغال جمهورية أفريقيا الوسطى تعديل مصدري - تعديل العلاقات السنغالية الوسط أفريقية هي العلاقات الثنائية التي تجمع بين السنغال وجمهورية أفريقيا الوسطى.[1][2][3][4][5] مقارن...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

«Questa è la Scuola della Fanteria, Regina delle battaglie» (All'ingresso della Scuola di Fanteria di Cesano) Fregio dell'Arma di Fanteria dell'Esercito Italiano (usato per la Fanteria di Linea) L'Arma di fanteria è un'Arma dell'Esercito Italiano che impiega combattenti appiedati, detti appunto i fanti. Viene considerata come l'ossatura della forza armata in quanto la maggioranza dei suoi reparti di manovra appartengono proprio all'arma. Indice 1 Storia 2 Caratteristiche 3 Specialità 3....

Umm Salama Hind bint Abi Umayya FöddMekkaDödMedinaBegravdAl-Baqi'MakeAbu Salama 'Abd Allah ibn 'Abd al-Asad al-Makhzumi(g. –625, makas/makes död)[1]Muhammed(g. 629–632, makas/makes död)[1]BarnZaynab bin Abi-SalamaRuqayyahSalama ibn Abi-SalamaZarahUmar ibn Abi-Salama (f. 620)FöräldrarAbu Umayya ibn Al-Mughira[1]Atikah bint ʿAmir ibn Rabi'ah[2]SläktingarKhalid ibn al-WalidRedigera Wikidata Umm Salama Hind bint Abi Umayya (arabiska: أُمّ سَلَمَة هِنْد بِنْت أَ�...

1984 split album by Helloween, Hellhammer, Running Wild, and Dark Avenger Death MetalCompilation album by Helloween, Hellhammer, Running Wild, and Dark AvengerReleasedMay 1984RecordedFebruary–March 1984 at Caet Studio, BerlinGenre Heavy metal speed metal thrash metal power metal black metal Length32:29LabelNoiseProfessional ratingsReview scoresSourceRatingRock Hard7.5/10[1] Death Metal is a 1984 split album by the heavy metal bands Helloween, Hellhammer, Running Wild, and Dark A...

كلارك سبنسر معلومات شخصية الميلاد 6 أبريل 1963 (61 سنة) سياتل مواطنة الولايات المتحدة الحياة العملية المدرسة الأم جامعة هارفارد المهنة منتج أفلام الجوائز جائزة الأوسكار لأفضل فيلم رسوم متحركة (عن عمل:زوتوبيا) (2015) جائزة الأوسكار لأفضل فيلم رسوم مت...
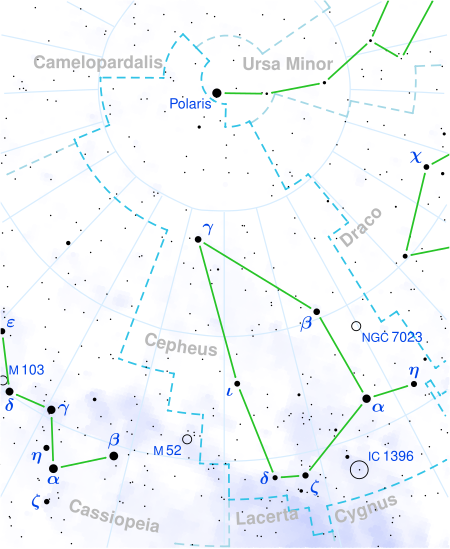
Star in the constellation Cepheus λ Cephei Location of λ Cep (circled) Observation dataEpoch J2000.0 Equinox J2000.0 Constellation Cepheus Right ascension 22h 11m 30.57571s[1] Declination +59° 24′ 52.15″[1] Apparent magnitude (V) +5.050[2] Characteristics Evolutionary stage Blue supergiant Spectral type O6.5If(n)p[3] U−B color index −0.622[2] B−V color index +0...

Jianzhi Sengcan Informasi Tanggal lahir: ? Tempat lahir: China Tanggal wafat: 606 Kewarganegaraan: Cina Sekolah: Ch'an Gelar: Patriark ke-3 Predecessor(s): Dazu Huike Successor(s): Dayi Daoxin Website Portal Buddhisme Jianzhi Sengcan (Tionghoa: 僧璨) (-606)? (Wade-Giles: Chien-chih Seng-ts'an; Jepang: Kanchi Sosan) dikenal sebagai Patriark ketiga Chán setelah Bodhidharma dan Patriark ketigapuluh setelah Buddha Siddhartha. Dia dianggap sebagai penerus Dharma dari Patriark Cina kedua, Dazu ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2020) حق_الفلسطينيين_في_تقرير_المصيرمعلومات عامةالمؤلف الأمير الحسن بن طلالاللغة الإنجليزيةالناشر دار مطبوعات كوورتيتتاريخ الإصدار 1981التقديمعدد الصفحات 148المع...

![{\displaystyle a={\sqrt[{3}]{\frac {GMT^{2}}{4\pi ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc0794d19344d83b82ba93518c68a0fccd0b31b)





