–•–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є—З–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П –≤–Є–њ–∞–і–Ї–Њ–≤–Њ—Ч –≤–µ–ї–Є—З–Є–љ–Є
|
Read other articles:

Untuk sinetron dengan judul yang mirip secara homofonik, lihat Bintang di Hatiku. Bintang di HatiSingel oleh Melly GoeslawDirilis7 September 2018 (2018-09-07)Direkam2018Genre Pop Durasi4:23LabelIndependenPenciptaMelly GoeslawProduser Melly Anto Hoed Kronologi singel Melly Goeslaw Lagu Religi (2018) Bintang di Hati (2018) Kusadari (2019) Video musikBintang di Hati di YouTube Bintang di Hati adalah lagu yang ditulis dan dinyanyikan oleh Melly Goeslaw yang dirilis pada tanggal 7 September 2...

Town in South AustraliaBalhannahSouth AustraliaOnkaparinga Valley Road at BalhannahBalhannahCoordinates34¬∞59вА≤S 138¬∞49вА≤E / 34.983¬∞S 138.817¬∞E / -34.983; 138.817Population1,660 (UCL 2021)[1]Established1839Location30 km (19 mi) SE of AdelaideLGA(s)Adelaide Hills CouncilState electorate(s)KavelFederal division(s)Mayo Localities around Balhannah: Carey Gully Lenswood Oakbank Mount George Balhannah Nairne Bridgewater Hahndorf Littlehampton Balhanna...

Finnish ice hockey player Ice hockey player Ville Lajunen Lajunen in 2023, while with the L√ґwen FrankfurtBorn (1988-03-08) 8 March 1988 (age 36)Helsinki, FinlandHeight 6 ft 0 in (183 cm)Weight 185 lb (84 kg; 13 st 3 lb)Position DefenceShoots RightDEL teamFormer teams L√ґwen FrankfurtEspoo BluesMetallurg MagnitogorskF√§rjestad BKJokeritSpartak MoscowKunlun Red StarHC VityazHC TPSSchwenninger Wild WingsNational team FinlandPlaying career 2007–...

–°–Є–±–Є—А—Б–Ї–Є–є –≥–Њ—А–љ—Л–є –Ї–Њ–Ј—С–ї –Э–∞—Г—З–љ–∞—П –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П –Ф–Њ–Љ–µ–љ:–≠—Г–Ї–∞—А–Є–Њ—В—Л–¶–∞—А—Б—В–≤–Њ:–Ц–Є–≤–Њ—В–љ—Л–µ–Я–Њ–і—Ж–∞—А—Б—В–≤–Њ:–≠—Г–Љ–µ—В–∞–Ј–Њ–Є–С–µ–Ј —А–∞–љ–≥–∞:–Ф–≤—Г—Б—В–Њ—А–Њ–љ–љ–µ-—Б–Є–Љ–Љ–µ—В—А–Є—З–љ—Л–µ–С–µ–Ј —А–∞–љ–≥–∞:–Т—В–Њ—А–Є—З–љ–Њ—А–Њ—В—Л–µ–Ґ–Є–њ:–•–Њ—А–і–Њ–≤—Л–µ–Я–Њ–і—В–Є–њ:–Я–Њ–Ј–≤–Њ–љ–Њ—З–љ—Л–µ–Ш–љ—Д—А–∞—В–Є–њ:–І–µ–ї—О—Б—В–љ–Њ—А–Њ—В—Л–µ–Э–∞–і–Ї–ї–∞—Б—Б:–І–µ—В–≤–µ—А–Њ–љ–Њ–≥–Є–µ–Ъ–ї–∞–і–∞:–Р–Љ–љ–Є–Њ—В—Л–Ъ–ї–∞–і–∞:–°–Є–љ–∞–њ—Б–Є–і—Л–Ъ–ї–∞пњљ...

–Ш–µ—А—Г—Б–∞–ї–Є–Љ—Б–Ї–Є–є –њ–∞—В—А–Є–∞—А—Е–∞—В–≥—А–µ—З. ќ†ќ±ѕДѕБќєќ±ѕБѕЗќµќѓќњќљ ќЩќµѕБќњѕГќњќїѕНќЉѕЙќљ –∞—А–∞–±. ўГўОўЖўРўКЎ≥ўОЎ© Ў£ўПўИЎ±ўПЎіўОўДўРўКўЕўО ЎІўДЎ£ўПЎ±ўТЎЂўПўИЎ∞ўПўГЎ≥ўРўКўОўСЎ© –Є–≤—А. „Ф„Ы„†„Щ„°„Щ„Щ„Ф „Ф„Р„Х„®„™„Х„У„Х„І„°„Щ„™ „©„Ь „Щ„®„Х„©„Ь„Щ„Э –•—А–∞–Љ –У—А–Њ–±–∞ –У–Њ—Б–њ–Њ–і–љ—П, –Ш–µ—А—Г—Б–∞–ї–Є–Љ –Ю–±—Й–Є–µ —Б–≤–µ–і–µ–љ–Є—П –Ю—Б–љ–Њ–≤–∞—В–µ–ї–Є –Р–њ–Њ—Б—В–Њ–ї—Л (—Б–Њ–≥–ї–∞—Б–љ–Њ —Ж–µ—А–Ї–Њ–≤–љ–Њ–Љ—Г –њ—А–µ–і–∞–љ–Є—О) –Ю—Б–љ–Њ–≤–∞–љ–Є–µ I –≤–µ–Ї –Ъ–Њ–љ—Д–µ...

Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Tafsir Akidah Fikih Syariat Sejarah Garis waktu Muhammad Ahlulbait Sahabat Nabi Khulafaur Rasyidin Khalifah Imamah Ilmu pengetahuan Islam abad pertengahan Penyebaran Islam Penerus Muhammad Budaya dan masyarakat Akademik Akhlak Anak-anak Dakwah Demografi Ekonomi Feminisme Filsafat...

Fianna F√°il вАУ Parti r√©publicain (en) Fianna F√°il вАУ The Republican Party(ga) Fianna F√°il вАУ An P√°irt√≠ Poblacht√°nach Logotype officiel. Pr√©sentation Chef Miche√°l Martin Fondation 23 mars 1926 Scission de Sinn F√©in Si√®ge 65вАУ66 Lower Mount Street Dublin (Irlande) Fondateur √Йamon de Valera Mouvement de jeunesse √Уgra Fianna F√°il Positionnement Centre droit[1] Id√©ologie Nationalisme irlandais D√©mocratie chr√©tienne Conservatisme Populisme Europhilie Troisi√®me voie Affiliatio...

ж≠§жҐЭзЫЃйЬАи¶Би°•еЕЕжЫіе§ЪжЭ•жЇРгАВ (2021еєі7жЬИ4жЧ•)иѓЈеНПеК©и£ЬеЕЕе§ЪжЦєйЭҐеПѓйЭ†жЭ•жЇРдї•жФєеЦДињЩзѓЗжЭ°зЫЃпЉМжЧ†ж≥ХжЯ•иѓБзЪДеЖЕеЃєеПѓиГљжЬГеЫ†зВЇеЉВиЃЃжПРеЗЇиАМ襀粿йЩ§гАВиЗідљњзФ®иАЕпЉЪиѓЈжРЬ糥дЄАдЄЛжЭ°зЫЃзЪДж†ЗйҐШпЉИжЭ•жЇРжРЬ糥пЉЪзЊОеЫљдЉЧиЃЃйЩҐ — зљСй°µгАБжЦ∞йЧїгАБдє¶з±НгАБе≠¶жЬѓгАБеЫЊеГПпЉЙпЉМдї•ж£АжЯ•зљСзїЬдЄКжШѓеР¶е≠ШеЬ®иѓ•дЄїйҐШзЪДжЫіе§ЪеПѓйЭ†жЭ•жЇРпЉИеИ§еЃЪжМЗеЉХпЉЙгАВ зЊОеЬЛзЬЊи≠∞йЩҐ United States House of Representativesзђђ118е±КзЊОеЫљеЫљдЉЪдЉЧиЃЃйЩҐеЊљзЂ† дЉЧиЃЃйЩҐжЧЧ...

Australian racing driver Cameron McConvilleMcConville in 2010Nationality AustralianBorn22 January 1974 (1974-01-22) (age 50)Melbourne, VictoriaSupercars careerDebut season1999TeamsJohn Faulkner RacingRod Nash RacingLansvale Racing TeamGarry Rogers MotorsportPaul Weel RacingBrad Jones RacingHolden Racing TeamLucas Dumbrell MotorsportStarts330Wins2Poles0Best finish10th in 2005Previous series19901991вАУ9219961997вАУ982011вАУ122012-172015,17Victorian Formula FordAustralian Formula FordA...

Arswendo Atmowiloto, pemimpin redaksi Monitor saat itu, yang mencetuskan ide angket Kagum 5 Juta Pada tahun 1990, Majalah Monitor pernah melakukan sebuah angket yang diberi nama Kagum 5 Juta. Angket tersebut pada dasarnya hanya ingin mengetahui siapakah tokoh yang dikagumi oleh pembaca Majalah Monitor pada saat itu sekaligus menambah oplah majalah yang saat itu disebut sebagai majalah dengan oplah tertinggi di Indonesia (Tempo, 27 Oktober 1990).[1][2][3] Angket ini jug...

гГ®гГПгГНгВє12дЄЦ зђђ130дї£ гГ≠гГЉгГЮжХЩзЪЗ жХЩзЪЗе∞±дїї 955еєі12жЬИ16жЧ•жХЩзЪЗйЫҐдїї 964еєі5жЬИ14жЧ•еЕИдї£ гВҐгВђгГЪгГИгВ•гВє2дЄЦжђ°дї£ гГђгВ™8дЄЦеАЛдЇЇжГЕ冱еЗЇзФЯ 937еєігВєгГЭгГђгГЉгГИеЕђеЫљпЉИдЄ≠йГ®гВ§гВњгГ™гВҐпЉЙгВєгГЭгГђгГЉгГИж≠їеОї 964еєі5жЬИ14жЧ• жХЩзЪЗй†ШгАБгГ≠гГЉгГЮеОЯеЫљз±Н гВєгГЭгГђгГЉгГИеЕђеۚ趙 зИґгВҐгГЂгГЩгГ™гГЉгВ≥2дЄЦпЉИгВєгГЭгГђгГЉгГИеЕђпЉЙгАБжѓНгВҐгГЂгГАгБЭгБЃдїЦгБЃгГ®гГПгГНгВєгГЖгГ≥гГЧгГђгГЉгГИгВТи°®з§Ї гГ®гГПгГНгВє12дЄЦпЉИIoannes XIIгАБ937еєі - 964еєі5жЬИ14жЧ•пЉЙгБѓгАБгГ≠...

жЬђжЦЗи®Шињ∞дЄАй†ЕдЄ≠еЬЛе§ІйЩЄжЦ∞иБЮеЛХжЕЛгАВйЪПзЭАдЇЛжЕЛиЃКеМЦпЉМеЕІеЃєжИЦи®±жЬГињЕйАЯжЫіжЦ∞гАВзґ≠еЯЇзЩЊзІСдЄНжШѓжЦ∞иБЮзЪДжФґйЫЖе§ДгАВиЂЛзХЩењГи®ШиЉЙж≠£зҐЇи≥Зи®КпЉМеЬ®жГЕ冱зЫЄе∞НжШОжЬЧеЊМзЈ®иЉѓжЫіжЦ∞гАВзЈ®иЉѓжЩВиЂЛдЊЭеПѓдЊЫжЯ•и≠ЙжЦєйЗЭпЉМзЫ°еПѓиГљйЩДдЄКдЊЖжЇРгАВ жЬђжЭ°зЫЃжШѓдє†ињСеє≥з≥їеИЧзЪДдЄАйГ®еИЖ еЕЪжАїдє¶иЃ∞гГїжЬАйЂШйҐЖеѓЉдЇЇгГїйҐЖеѓЉж†ЄењГ дЄ≠еЕ±еНБеЕЂе§І 2012еєіељУйАЙжАїдє¶иЃ∞ дЄ≠еЕ±еНБдєЭе§І 2017еєіињЮдїїжАїдє¶иЃ∞ 2018еєідњЃжФєеЃ™ж≥Х дЄ≠еЕ±дЇМеНБе§І 2022еєіеЖНдїїжАїдє¶иЃ∞ зњТињСеє≥...

Chaz Bowyer Raymond Chaz Bowyer (29 September 1926 вАУ 18 June 2008) was a Royal Air Force armaments and explosives instructor who, after he retired from service, wrote and edited over forty books relating to the operations, aircraft, and men of the Royal Flying Corps, Royal Air Force, and Royal Naval Air Service. He also edited for publication the memoirs of the pilots C.P.O. Bartlett, Eric Crundall, and Gwilym H. Lewis. Early life and family Chaz Bowyer was born in Weymouth, Dorset, on 29 ...

AustralopithecusRentang fosil: Miocene - Pleistocene 6.1вАУ1.2 jtyl Pre–Д –Д O S D C P T J K Pg N ↓ Australopithecus sediba Klasifikasi ilmiah Kerajaan: Hewan Filum: Chordata Kelas: Mamalia Infrakelas: Eutheria Ordo: Primata Famili: Hominidae Subfamili: Homininae Tribus: Hominini Subtribus: Australopithecina Genera Australopithecus Paranthropus Ardipithecus (didiskusikan[1]) Orrorin (yang paling disukai) Sahelanthropus (mungkin) Istilah australopithecine secara umum meruju...

1937 film The CheatFrenchForfaiture Directed byMarcel L'HerbierWritten byJean-Georges AuriolJacques Compan√©ezHerbert JuttkeJacques NatansonHector TurnbullProduced byMichael SalkindPierre BraunbergerAyres d'AguiarRoger Richeb√©StarringVictor FrancenSessue HayakawaLouis JouvetCinematographyEugen Sch√ЉfftanEdited byPierre de H√©rainMarie Le BarsMusic byMichel MicheletProductioncompanySoci√©t√© du Cin√©ma du Panth√©onDistributed byGray-FilmRelease date 24 November 1937 (1937-11-24...
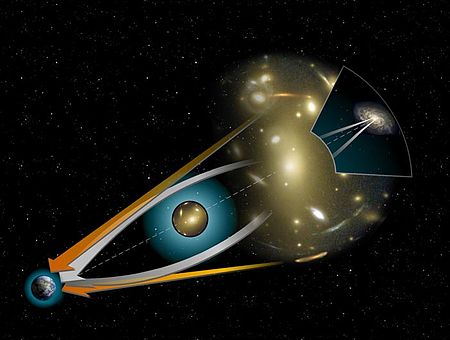
Lentille gravitationnelle pleine. Une √©toile √† pr√©on est un type dвАЩ√©toile compacte hypoth√©tique constitu√©e de pr√©ons, un groupe de particules subatomiques elles-m√™mes hypoth√©tiques. Les √©toiles √† pr√©on devraient avoir une densit√© √©norme, sup√©rieure √† 1023 kg/m3. Il sвАЩagit dвАЩun chiffre interm√©diaire entre les √©toiles √† quarks et les trous noirs. Une √©toile √† pr√©on dвАЩune masse comparable √† celle de la Terre aurait ainsi la taille dвАЩune balle de tennis. Les √©toi...

English singer (born 1989) Jess GlynneGlynne performing at South by Southwest in 2015BornJessica Hannah Glynne (1989-10-20) 20 October 1989 (age 34)Hampstead, London, EnglandOccupations Singer songwriter Years active2013вАУpresentWorksDiscographyMusical careerGenres Pop R&B[1] dance soul Instrument(s)VocalsLabels EMI Black Butter Atlantic Websitejessglynne.co.uk Musical artist Jessica Hannah Glynne (born 20 October 1989) is an English singer and songwriter. After signing...

Room with large glass windows or walls for exposure to sunlight Sun lounge redirects here. For the streamlined sleeper-lounge car, see Sun Lounge (railcar). For the outdoor furniture, see Sunlounger. For the American rock band, see Sun Room. Florida room redirects here. For the Donald Fagen song, see Kamakiriad ¬І Track listing. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be cha...

The 2014 Kerrick Sports Sedan Series was an Australian motor racing competition open to Sports Sedans and Trans Am style cars.[1] It was sanctioned by the Confederation of Australian Motor Sport as a National Series[1] and was the eleventh National Series for Sports Sedans contested following the discontinuation of the Australian Sports Sedan Championship at the end of 2003. The 2014 series was won by Tony Ricciardello driving an Alfa Romeo GTV. Calendar Tony Ricciardello plac...

Laurence TubianaLaurence Tubiana en 2016.FonctionsPr√©sidente du directoireAgence fran√Іaise de d√©veloppement2013-2022Pr√©sidenteInstitut du d√©veloppement durable et des relations internationales2002-2014Teresa RiberaBiographieNaissance 5 juillet 1951 (73 ans)Oran (Alg√©rie fran√Іaise)Nom de naissance √Йmilie Laurence TubianaNationalit√© fran√ІaiseFormation Institut d'√©tudes politiques de Paris (jusqu'en 1973)Universit√© Paris-I-Panth√©on-Sorbonne (doctorat)Activit√©s √Йconomiste, pro...
















![{\displaystyle X\sim U[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3610abb42eb437d4b299a01c755ba35989970ea)














































