Універсум фон Неймана
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Ekspress AM4R (Rusia: Экспресс-АМ4Р makna Ekspress AM4R) adalah komunikasi satelit Rusia dimaksudkan untuk operasi oleh Perusahaan Negara Komunikasi Satelit. Ekspress AM4R hilang karena kegagalan peluncuran. Referensi Krebs, Gunter. Ekspress...

Mary J. Blige Mary Jane Blige (lahir 11 Januari 1971) merupakan seorang penyanyi, penulis lagu, rapper dan aktris berkebangsaan Amerika Serikat. Namanya dikenal sebagai Queen of Hip Hop Soul. Dia dilahirkan di Yonkers, New York. Dia berkarier di dunia musik sejak tahun 1989. Pada tahun 1992, Blige merilis album pertamanya, What's the 411? [4] Albumnya pada 1994 My Life adalah di antara 500 Album Terbesar Sepanjang Masa milik Rolling Stone, dan Album Sepanjang Masa 100 Album Time. Dia menerima...

Canadian human rights activist This article may have been created or edited in return for undisclosed payments, a violation of Wikipedia's terms of use. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. (March 2020) Craig KielburgerCM MSM OMCKielburger in 2011BornCraig Kielburger (1982-12-17) December 17, 1982 (age 41)Thornhill, Ontario, CanadaNationalityCanadianEducation Trinity College, Toronto (BA) York University (MBA) Occ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sunamganj District – news · newspapers · books · scholar · JSTOR (March 2012) (Learn how and when to remove this template message) District of Bangladesh in Sylhet DivisionSunamganj District সুনামগঞ্জ জেলাDistrict of BangladeshSunamgan...

As-Sayid As-SyarifRaden Sayid Maulana Makhdum Ibrahim ( Sunan Bonang ) (Bong Tak An) Imam Masjid Demak Ke - 1Masa jabatan1490 – 1506/12 (?) PendahuluJabatan BaruPenggantiRaden Sayid Maulana Makhdum Husein / Sayid Husein ( 1506/12 (?) - 1515 ) Informasi pribadiLahirMaulana Makhdum Ibrahim1465 (1465)RembangMeninggal1525Tuban, Kesultanan DemakAgamaIslamAnakd Maulana Makhdum Husein / Sayid Husein (Makhdum Sampang)Orang tuaSunan Ampel (ayah)Nyai Ageng Manila (ibu)DenominasiSunniDik...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة ...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Manajer tim nasional sepak bola Inggris di en.wikipedia.org. Isinya masih belum ...

Major League Baseball season Major League Baseball team season 2009 Baltimore OriolesLeagueAmerican LeagueDivisionEastBallparkOriole Park at Camden YardsCityBaltimoreRecord64–98 (.395)Divisional place5thOwnersPeter AngelosGeneral managersAndy MacPhailManagersDave TrembleyTelevisionMASNWJZ-TV (CBS 13)RadioWHFS ← 2008 Seasons 2010 → The Baltimore Orioles' 2009 season was the 109th season in franchise history. The Orioles finished the season last in the AL East with ...

TimișoaraKotaTimișoara Lambang kebesaranJulukan: Little Vienna (bahasa Rumania: Mica Vienă), City of Flowers (Orașul Florilor), Heart of Banat (Inima Banatului)[1]Kota TimisoaraTimișoaraLocation of Timișoara within RomaniaKoordinat: 45°45′35″N 21°13′48″E / 45.75972°N 21.23000°E / 45.75972; 21.23000Koordinat: 45°45′35″N 21°13′48″E / 45.75972°N 21.23000°E / 45.75972; 21.23000Kota Rumani...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Pour l’article homonyme, voir Indian Grove. Indian Motorcycle Company Le logo actuel de la marque. Création 1901 Fondateurs George M. HendeeOscar Hedström Personnages clés Stephen JuliusSteve Heese Forme juridique Société à responsabilité limitée Siège social Medina (Minnesota) États-Unis Activité Construction de véhicules automobiles, de remorques et semi-remorques Produits Motos Société mère Polaris Industries Sociétés sœurs Victory Motorcycles Filiales Victory Mot...

Identity ThiefPoster resmiSutradaraSeth GordonProduserScott StuberPamela AbdySkenarioCraig MazinCeritaJerry EetenCraig MazinPemeranJason BatemanMelissa McCarthyPenata musikChristopher LennertzSinematograferJavier AguirresarobePenyuntingPeter TeschnerPerusahaanproduksiRelativity MediaScott Stuber ProductionsAggregate FilmsBluegrass FilmsDistributorUniversal PicturesTanggal rilis 08 Februari 2013 (2013-02-08) Durasi112 Menit[1]NegaraAmerika SerikatBahasaInggrisAnggaran$35 Jut...

2019 Canadian film directed by Louise Archambault And the Birds Rained DownFilm posterFrenchIl pleuvait des oiseaux Directed byLouise ArchambaultWritten byLouise ArchambaultBased onIl pleuvait des oiseaux by Jocelyne SaucierProduced byGinette PetitStarringRémy GirardGilbert SicotteAndrée LachapelleÈve LandryCinematographyMathieu LaverdièreEdited byRichard ComeauProductioncompanyLes Films OutsidersDistributed byMK2 Mile EndIndie SalesRelease date September 7, 2019 (2019-09-0...

Sporting event delegationRussia at the2016 Summer OlympicsIOC codeRUSNOCRussian Olympic CommitteeWebsitewww.olympic.ru (in Russian)in Rio de JaneiroCompetitors282 in 26 sportsFlag bearers Sergey Tetyukhin (opening)[1]Natalia Ishchenko and Svetlana Romashina (closing)MedalsRanked 4th Gold 19 Silver 17 Bronze 20 Total 56 Summer Olympics appearances (overview)1996200020042008201220162020–2024Other related appearances Russian Empire (1900–1912) Soviet Union (1952�...

جائزة إسبانيا الكبرى 1990 (بالإسبانية: XXXI Gran Premio Tio Pepe de España) السباق 14 من أصل 16 في بطولة العالم لسباقات الفورمولا واحد موسم 1990 السلسلة بطولة العالم لسباقات فورمولا 1 موسم 1990 البلد إسبانيا التاريخ 30 سبتمبر 1990 مكان التنظيم شريش، إسبانيا طول المسار 4.218 كيلومتر (2.6209 م...

بنك الاحتياطي الأسترالي البلد أستراليا تاريخ إنشاء 14 يناير 1960[1] الرئيس Philip Lowe العملة دولار أسترالي الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل بنك الاحتياطي الأسترالي ( RBA ) هو البنك المركزي لأستراليا والمصدر الرئيسي للأوراق النقدية. لقد كان ل...
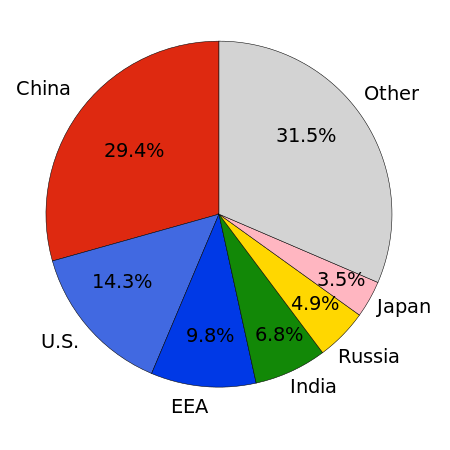
Interaction of societies and governments with modern climate change For the politicisation or debate over climate change, see Global warming controversy. Heads of delegations at the 2015 United Nations Paris conference The politics of climate change results from different perspectives on how to respond to climate change. Global warming is driven largely by the emissions of greenhouse gases due to human economic activity, especially the burning of fossil fuels, certain industries like cement ...

1993 studio album by Tom WaitsThe Black RiderStudio album by Tom WaitsReleasedSeptember 1993 (1993-09)Recorded1989, 1993Genre Experimental avant-garde chamber rock Dark Cabaret Length56:08LabelIslandProducerTom WaitsTom Waits chronology Bone Machine(1992) The Black Rider(1993) Mule Variations(1999) Professional ratingsReview scoresSourceRatingAllMusic[1]Chicago Tribune[2]Entertainment WeeklyB[3]Los Angeles Times[4]Mojo[5]NME8/10[6&...

American actor (born 1954) Denzel WashingtonWashington in 2018BornDenzel Hayes Washington Jr. (1954-12-28) December 28, 1954 (age 69)Mount Vernon, New York, U.S.EducationFordham University (BA)American Conservatory TheaterOccupationsActordirectorproducerYears active1975–presentWorksFull listSpouse Pauletta Pearson (m. 1983)Children4, including John David and OliviaAwardsFull listHonorsPresidential Medal of Freedom (2022) Denzel Hayes Washington Jr. ...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يناير 2022) احتراق ...

































