Система відліку
| ||||||||||||||||||||
Read other articles:

Gusle Gusle (bahasa Serbia: гусле; bahasa Bulgaria: гусла) atau lahuta (bahasa Albania: lahutë) adalah alat musik bersenar tunggal (dan gaya musik) yang secara tradisional digunakan di wilayah Dinarides di Eropa Tenggara (di Balkan). Instrumen selalu diiringi dengan nyanyian; cerita rakyat musikal, khususnya puisi epik. Pemain gusle memegang instrumen secara vertikal di antara lututnya, dengan jari-jari tangan kiri di senar. Senar tidak pernah ditekan ke leher, memberik...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Raijin-2 (Rising-2) adalah mikro-satelit Jepang diluncurkan pada 2014. Satelit itu dibangun di sekitar diameter 10 cm. Referensi RISING-2 mission equipment Diarsipkan 2016-03-03 di Wayback Machine. Eoportal RISING-2 page

Arsitektur Mughal Taj Mahal, Agra, adalah struktur arsitektur Mughal yang paling dikenal. Masjid Badshahi, Lahore, Pakistan adalah masjid terbesar di dunia selama 313 tahun, dan saat ini merupakan masjid terbesar kedua di Asia Selatan. Masjid Jama, Delhi, masjid terbesar di India. Buland Darwaza, Agra dibangun oleh Akbar Agung untuk memperingati kemenangannya. Benteng Merah, Delhi, tempat tinggal dinasti Mughal. Makam Humayun, Delhi. Gerbang Alamgiri di Benteng Lahore, Lahore, Pakistan. Maka...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Nottingham ForestNama lengkapNottingham Forest YesJulukanForest, The Reds, NFFC, The Tricky Trees,[1] '[2]Berdiri1865StadionCity GroundWest BridgfordNottingham(Kapasitas: 30,602[3])Pemilik Evangelos MarinakisKetua Nicholas Randall QC[4]Manajer Nuno Espírito SantoLigaLiga Utama Inggris2022–2023Liga Utama Inggris, ke-16 dari 20Situs webSitus web resmi klub Kostum kandang Kostum tandang Kostum ketiga Musim ini Nottingham Forest Football Club adalah nama kl...

Плотность населения Финляндии по муниципалитетам, человек на квадратный километр Возрастно-половые пирамиды населения Финляндии в 1972—2020 года. Население финского происхождения изображено в цвете, иностранного — серым цветом. Возрастно-половая пирамида населени�...
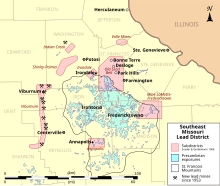
Not to be confused with the Tri-State District, another lead mining district also largely located in Missouri. Lead mining area in Missouri, US Lead belt redirects here. For the concentration of wargames companies in England, see Lead belt (wargaming). Map of counties in the regionNotable subdistricts of the Lead Belt and the mines of the New Lead Belt Historical marker commemorating the first mine at Mine La Motte about 1700. Missouri Mines State Historic Site occupies a retired lead mill in...

العلاقات السنغالية المالية السنغال مالي السنغال مالي تعديل مصدري - تعديل العلاقات السنغالية المالية هي العلاقات الثنائية التي تجمع بين السنغال ومالي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة السنغا�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: John Bowne High School – news · newspapers · books · scholar · JSTOR (May 2011) (Learn how and when to remove this template message) Public school in Flushing, Queens, New York, United StatesJohn Bowne High SchoolAddress63-25 Main StFlushing, Queens, New York 1...
Untuk kegunaan lain, lihat Republik (disambiguasi). Bagian dari seri PolitikBentuk dasar dari pemerintahan Struktur kekuatan Konfederasi Federasi Hegemoni Kerajaan Negara kesatuan Sumber kekuatan Demokrasi Langsung Perwakilan Semi lainnya Kerajaan Mutlak Konstitusi Oligarki Aristokrasi Junta militer Kleptokrasi Plutokrasi Stratokrasi Timokrasi Otokrasi Otoritarianisme Despotisme Diktatur (Kediktatoran) Totalitarianisme Republik Parlementer Presidensial Semi presidensial Lainnya Anarki An...

Ruling party of the Turkmen SSR (1924–1991) For the party founded in 1998, see Communist Party of Turkmenistan (1998). You can help expand this article with text translated from the corresponding article in Russian. (February 2013) Click [show] for important translation instructions. View a machine-translated version of the Russian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary a...

Sungai SipaiSungai SipaiLokasi mulut sungaiTampilkan peta KalimantanSungai Sipai (Indonesia)Tampilkan peta IndonesiaLokasiNegaraIndonesiaProvinsiKalimantan SelatanCiri-ciri fisikHulu sungai - lokasiKalimantan Sungai Sipai atau Sungai Sifa adalah sungai yang mengalir di kota Banjarmasin, Kalimantan Selatan, Indonesia. Geografi Sungai ini mengalir di kecamatan Banjarmasin Tengah.[1] Sungai Sipai memiliki panjang 404,455 m dengan lebar 10-12 m.[2] Lihat pula Dafta...

Wharfside at St. Johns. The shedlike structure behind the reservists is a drill hall erected atop Calypso's gunwale. Boat davits are shown on port side of vessel (upper left) and at stern (far right); the aft port 6 gun is sponsoned out from the hull (right of top rows of sailors).Image from Provincial Archives of Newfoundland and Labrador Pancake Rock at Fort Amherst, visible to left from Signal Hill. Fort Waldegrave was a battery or an emplacement for heavy guns in St. John’s Newfoundland...

Historic district in Georgia, United States United States historic placeDungeness Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district Dungeness in 1958Show map of GeorgiaShow map of the United StatesNearest citySt. Marys, GeorgiaArchitectMultipleArchitectural styleQueen Anne, Shingle StyleMPSCumberland Island National Seashore MRANRHP reference No.84000920Added to NRHPFebruary 13, 1984[1] Dungeness on Cumberland Island, Georgia, is a ruined ...

Azania Front Lutheran Church St Joseph's Catholic cathedral, Zanzibar Christianity is the most widely professed religion in Tanzania, but in the island of Zanzibar most of the population is Muslim. Historical information Christianity was introduced in the 16th century when Franciscans established a mission in Kilwa.[1] Spiritan missionaries arrived in the area in 1868.[2] The Anglican mission was established in 1876.[3] The Christian Council of Tanzania was founded in...

Massiccio del Monte RosaVersante piemontese del massiccio visto dalla zona delle Alpi biellesi: a sinistra, la parete valsesiana, a destra, la parete est.ContinenteEuropa Stati Italia Svizzera Cima più elevataPunta Dufour (4 634 m s.l.m.) Massicci principaliCatena Breithorn-Lyskamm (1)Massiccio del Monte Rosa (2)Gruppo della Cima di Jazzi (3) Il Monte Rosa (o Massiccio del Monte Rosa[1], Monte Rosa o Monte-Rosa-Massiv in tedesco; Mont Rose o Massif du mont Ro...

Extremadura campaignPart of Spanish Civil WarDate2–14 August 1936LocationBadajoz Province, Extremadura, SpainResult Nationalist victoryBelligerents Spanish Republic Nationalist Spain[1] Regulares Spanish Legion Aviazione Legionaria Nazi GermanyCommanders and leaders Ildefonso Puigdendolas Juan Yagüe Carlos Asensio Antonio Castejón Fernando BarronStrength 13,000 militiamensome Breguet XIX bombers 8,000 regulars17 medium bombersCasualties and losses Unknown military dead6,600�...

British actress (1893–1977) For the American artist, see Margaret Ann Withers. Margaret Withers 1939 Spotlight photo Margaret Withers (6 July 1893 – 26 October 1977) was a British actress mainly on the stage.[1][2][3] Filmography Year Title Role Notes 1935 Car of Dreams Mrs. Hart 1943 The Demi-Paradise Mrs. Elliston Uncredited 1944 Don't Take It to Heart Mrs. Smith 1945 Great Day Miss Jane Tyndale 1945 The Seventh Veil Uncredited 1947 Dual Alibi Blackpool Landlady ...

181st (Airlanding) Field AmbulanceCap badge of the Royal Army Medical CorpsActive1941–1945CountryUnited KingdomBranchBritish ArmyTypeMedicalRoleAirborne forcesSizeField AmbulancePart of1st Airlanding BrigadeEngagementsOperation BitingOperation LadbrokeOperation SlapstickBattle of ArnhemOperation DoomsdayInsigniaAirborneforcesemblemMilitary unit The 181st (Airlanding) Field Ambulance was a Royal Army Medical Corps unit of the British airborne forces during the Second World War. The Fie...

2nd government of Francisco FrancoGovernment of Spain1939–1945Date formed9 August 1939Date dissolved20 July 1945People and organisationsHead of StateFrancisco FrancoPrime MinisterFrancisco FrancoNo. of ministers15[a] (1939–1940)14[a] (1940)13[a] (1940–1945)Total no. of members25[a]Member party National Movement (Military, FET–JONS, ACNP, nonpartisans)Status in legislatureOne-party stateHistoryLegislature term1st Cortes EspañolasBudget1940, 1942, ...
























![{\displaystyle \mathbf {v} =\mathbf {v} '+[\mathbf {\omega } \mathbf {r} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d6c0accec615aa125a3f8651742cd2bd272fb64)
![{\displaystyle \mathbf {a} =\mathbf {a} '+2[\mathbf {\omega } \mathbf {v} ']+[\mathbf {\omega } [\mathbf {\omega } \mathbf {r} ]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f46ce505ab4ee8b8c56d0e74a059834d70cebb47)










